РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА
1.ТЕРМОДИНАМІКА
Перший початок термодинаміки:
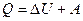
Тут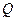 
- кількість теплоти, передана системі;
- зміна внутрішньої енергії системи;
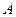- робота, що здійснюється системою.
Обмін речовин у живих організмах підкоряється цьому закону. Визначення енергетичного обміну між живими організмами і навколишнім середовищем здійснюється за допомогою калориметрії, яка підрозділяється на пряму і непряму. Поширенішою є непряма калориметрія. У цьому випадку про сумарний тепловий ефект реакцій, що протікають в організмі, судять за калориметричним коефіцієнтом кисню. Він показує, яка кількість теплоти виділяється при повному окисленні даної речовини до вуглекислого газу і води на кожен літр поглиненого організмом кисню. Встановлено, що цей коефіцієнт для вуглеводів рівний 20,9, для жирів – 19,7 і для білків – 20,3 кДж. Проте у живому організмі йде також синтез речовин, які потім можуть окислюватися. Щоб врахувати загальну кількість теплоти, що звільняється живим організмом за певний проміжок часу, треба враховувати дихальний коефіцієнт, рівний відношенню об'ємів вуглекислого газу до спожитого за той же час кисню. Дихальний коефіцієнт для вуглеців рівний 1, для білків – 0,8 і для жирів він складає 0,7. Існує зв'язок між дихальним і калориметричним коефіцієнтами ( таблиця 1.1). Це дозволяє встановлювати витрату енергії організму, знаючи кількість поглиненого кисню і виділеного вуглекислого газу.
Завдання 1.Визначити витрату енергії людини в стані м'язового спокою, якщо за 10 хвилин вона видихає 60 л повітря, в якому міститься 15 % кисню і 5 % вуглекислого газу.
Рішення: У атмосферному повітрі міститься близько 21 % кисню і 0,03 % вуглекислого газу. Отже, з кожних 100 мл повітря, що пройшли через легені людини, організмом поглинається:
21-15= 6 мл О2
Таблиця 1.1
Зв'язок калориметричного коефіцієнта 1 л кисню з дихальним коефіцієнтом
| Дихальний коефіцієнт | К.К., кДж | Дихальний коефіцієнт | К.К., кДж | Дихальний коефіцієнт | К.К., кДж | Дихальний коефіцієнт | К.К., кДж |
| 0.70 | 19,619 | 0,78 | 19,996 | 0,86 | 20,411 | 0,94 | 20,821 |
| 0,71 | 19,636 | 0,79 | 20,051 | 0,87 | 20,461 | 0,95 | 20,871 |
| 0,72 | 19,686 | 0,80 | 20,101 | 0,88 | 20,515 | 0,96 | 20,921 |
| 0,73 | 19,737 | 0,81 | 20,151 | 0,89 | 20,566 | 0,97 | 20,976 |
| 0,74 | 19,791 | 0,82 | 20,201 | 0,90 | 20,616 | 0,98 | 21,026 |
| 0,75 | 19,841 | 0,83 | 20,256 | 0,91 | 20,666 | 0,99 | 21,076 |
| 0,76 | 19,896 | 0,84 | 20,306 | 0,92 | 20,716 | 1,00 | 21,131 |
| 0,77 | 19,946 | 0,85 | 20,360 | 0,93 | 20,767 | - | - |
При цьому виділяється 5 мл СО2. Хвилинний об'єм дихання людини дорівнює:
60 л : 10 = 6 л
Для розрахунку кількості кисню, що поглинається людиною за хвилину, складаємо пропорцію:
з 100 мл повітря споживається - 6 мл О2
з 6000 мл – x
отже x = 360 мл О2.
Дихальний коефіцієнт визначаємо, виходячи з даних завдання:
ДК = СО2 / О2 = 5/6 = 0,83
З таблиці 1.1 знаходимо калориметричний коефіцієнт при даному дихальному коефіцієнті. Він дорівнює 20,26 кДж.
Витрата енергії людини в хвилину в стані м'язового спокою складає:
0,360·20,26 = 7,29 кДж
За 10 хвилин енергетична витрата складає 72,9 кДж.
Варіанти завдань наведені у таблиці 1.2
Таблиця 1.2
| № варіанту | час, хв. | об'єм, л | вміст кисню, % | вміст вуглекислого газу, % |
| 19,56 | ||||
| 15,65 | 3,56 | |||
| 20,5 | 5,2 | |||
| 15,7 | 5,3 | |||
| 16,52 | 5,4 | |||
| 14,95 | 5,5 | |||
| 5.6 | ||||
| 5,7 | ||||
| 5,8 | ||||
| 65,5 | 5,9 | |||
| 6,1 | ||||
| 51,5 | 6,5 | |||
| 7,1 | ||||
| 16,25 | 5,8 | |||
| 15,85 | 6,2 | |||
| 15,25 | 5,2 | |||
| 14,5 | ||||
| 14,25 | 5,1 | |||
| 17,52 | 5,5 | |||
| 5,3 | ||||
| 5,05 | ||||
| 5,25 | ||||
| 6,0 | ||||
| 5,90 | ||||
| 74,5 | 6,6 | |||
| 6,9 | ||||
| 6,65 | ||||
| 76,5 | 5,55 |
2. ВИКОРИСТАННЯ МЕТОДІВ МАТЕМАТИЧНОЇ СТАТИСТИКИ В МЕДИЧНІЙ ДІАГНОСТИЦІ
Математична статистика – наука про математичні методи систематизації і використання статистичних даних для вирішення наукових та практичних завдань|задач|.
Припустимо|передбачимо|, що необхідно вивчити безліч об'єктів, за якою-небудь ознакою. Це, можна зробити, провівши суцільне спостереження або вибіркове.
Велика статистична сукупність, з|із| якої відбирається частина|частка| об'єктів для дослідження, називається генеральною сукупністю, а безліч об'єктів, відібраних з|із| неї - вибіркою.
Якщо записати в послідовності вимірювань|вимірів| всі значення величини X у вибірці, то одержимо|отримаємо| простий статистичний ряд|лаву,низку|. Наприклад, зростання|зріст| чоловіків (см): 171,172,172,168,170,169. . Такий ряд|лава,низка| незручний для аналізу, оскільки|тому що| в ньому немає послідовності зростання (або убування) значень, зустрічаються і величини, що повторюються. Тому доцільно ранжирувати ряд|лаву,низку|, наприклад, у зростаючому порядку|ладі| значень і вказати їх повторюваність. Тоді статистичний розподіл вибірки:
,
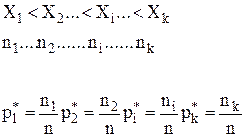де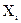 
- спостережувані значення ознаки; 
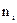- число спостережень варіанту 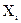(частота); 
- відносна частота.
Загальне|спільне| число об'єктів у вибірці (об'єм|обсяг| вибірки)
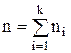
Тут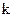 
- варіант. Статистичний розподіл – це сукупність варіантів і відповідних їм частот.
У медичній літературі статистичний розподіл, що складається з варіантів і відповідних їм частот, одержало|отримало| назву варіаційного ряду|лави,низки|.
Разом з|поряд з,поряд із| дискретним (точковим) статистичним розподілом, використовують безперервний (інтервальний) розподіл:
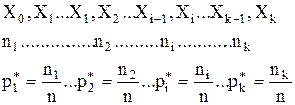
Тут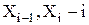 
-й інтервал, у якому розміщено|ув'язнено| кількісне значення ознаки; 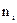- сума частот варіант, що потрапили|попали| в цей інтервал; 
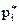- сума відносних частот.
Завдання 2
Задано статистичний розподіл маси новонароджених хлопчиків (кг) і частоти.
| 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 |
Загальна|спільна| кількість хлопчиків
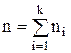=100
Представляємо|уявляємо| цей розподіл як безперервний
| 2,65-2,75 | 2,75-2,85 | 2,85-2,95 | 2,95-3,05 | 3,05-3,15 | … |
| … |
Представимо|уявимо| статистичний розподіл у вигляді полігону і гістограми.
Полігон частот – ламана лінія, відрізки якої сполучають|поєднують,з'єднують| крапки|точки| з|із| координатами ( 
), ( 
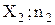), або для полігону відносних частот-| з|із| координатами ( 
), ( 
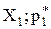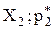) (малюнок 2.1).
Гістограма частот – сукупність суміжних прямокутників, побудованих|споруджених| на одній прямій лінії (малюнок 2.2), підстави прямокутників однакові і рівні а, а висоти рівні відношенню|ставленню| частоти (або відносної частоти) до а.
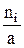або 
.
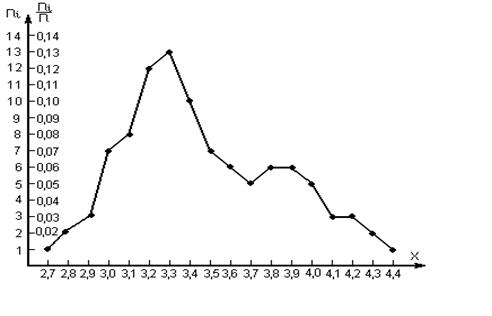
Малюнок 2.1 - Полігон частот
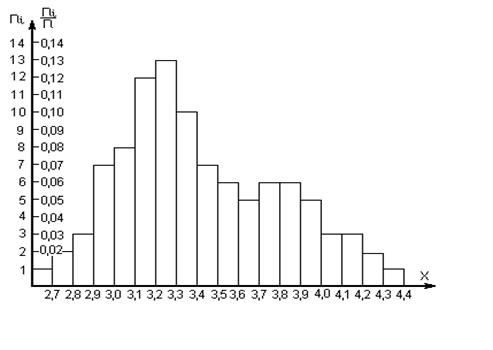
Малюнок 2.2 - Гістограма частот
Таким чином, площа|майдан| кожного прямокутника дорівнює відповідно:
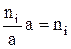або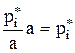 
.
Отже, площа|майдан| гістограми частот 
, а площа|майдан| гістограми відносних частот :
Розрахуємо моду, медіану і вибіркове середнє.
Мода (М0) рівна варіанті, якій відповідає найбільша частота. У розподілі
М0= 3,3 кг
Медіана (Ме) рівна варіанті, яка розташована|схильна| у середині статистичного розподілу. Вона ділить статистичний ряд|лаву,низку| на дві рівні частини. При парному числі варіант за медіану приймають середнє значення з|із| двох центральних варіант.
Ме = 3,4 кг
Вибіркова середня (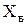 
) визначається як середнє арифметичне значення варіант статистичного ряду|лави,низки|:
або
= 
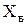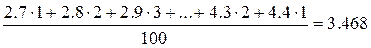кг.
Вибіркова дисперсія –середнє арифметичне квадратів відхилення варіант від їх середнього значення:
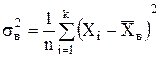
Квадратний корінь з|із| вибіркової дисперсії називають вибірковим середнім квадратичним відхиленням:
;
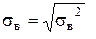
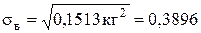кг
Розрахуємо виправлену|справлену| вибіркову дисперсію:
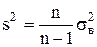
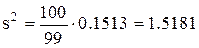1,2321.
Задаємо довірчу вірогідність|ймовірність| =0.95. З|із| таблиці 2.1 знаходимо|находимо| для заданих значень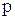 
=0.95 і 
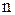=100 коефіцієнт Стьюдента 
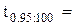2. Визначаємо|находимо| інтервал:
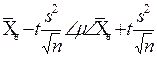
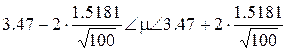
або 
.
Зробити висновки|виведення| за результатами |за результатами| роботи.
Таблиця 2.1 - Коефіцієнти Стьюдента
| n | р | |||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 0,16 | 0,33 | 0,51 | 0,73 | 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 0,82 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |||||
| 0,98 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | ||||||
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |||||||
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | |||||||
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 | |||||||
| 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,5 | |||||||
| 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 | |||||||
| 1,1 | 1,4 | 1,9 | 2,3 | 2,8 | 3,3 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,8 | 3,2 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,0 | |||||||
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 3,0 | |||||||
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 2,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,5 | 2,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,4 | 2,6 | |||||||
| до | 1,1 | 1,3 | 1,7 | 2,0 | 2,3 | 2,6 |
Варіанти завдань|задавань|:
1. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,5.
2. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,8.
3. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,95.
4. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,7
5. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,6.
| 1,9 | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
6. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,5.
| 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
7. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,4.
| 0,15 | 0,16 | 0,17 | 0,18 | 0,19 | 0,20 | 0,21 | 0,22 | 0,23 | 0,24 | 0,25 | 0,26 |
8. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,3.
9. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,2.
| 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,3 |
10. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,1.
| 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,1 | 0,11 | 0,12 | 0,13 | 0,14 |
11. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,95.
12. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,8.
13. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,7.
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 |
14. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,9.
15. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,6.
16. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,4.
17. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,9.
| 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,16 | 0,17 |
18. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,1.
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 |
19. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,3.
20. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,4.
21. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,3.
22. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,2.
23. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,1.
| 5,21 | 5,22 | 5,23 | 5,24 | 5,25 | 5,26 | 5,27 | 5,28 | 5,29 | 5,30 | 5,31 | 5,32 |
24. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,2.
| 7,0 | 7,1 | 7,2 | 7,3 | 7,4 | 7,5 | 7,6 | 7,7 | 7,8 | 7,9 | 8,0 | 8,1 |
25. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,5.
26. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,95.
27. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,8.
28. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,7.
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
29. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,4.
30. Задано статистичний розподіл. Довірча вірогідність|ймовірність| 0,1.
Дата добавления: 2015-03-14; просмотров: 859;