Рефракція радіохвиль у тропосфері

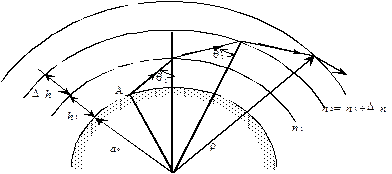
Залежність показника заломлення тропосфери (стратосфери) від висоти h супроводжується скривленням траєкторії поширення радіохвилі у відповідності до законів Снелліуса, тобто до законів геометричної оптики. Припустимо, що тропосфера складається з тонких сферичних шарів товщиною Dh, таких, що в межах кожного шару показник заломлення n залишається постійним, але змінюється від шару до шару на величину Dn (рис. 2.5, а). Нехай хвиля з точки А падає під кутом q₁ на шар із показником заломлення n₁. Припустимо, що значення показників заломлення подальших шарів менше попередніх значень. Тоді у відповідності до другого закону Снелліуса

,

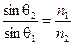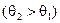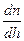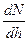тобто кути падіння на кожний наступний шар збільшуються і траєкторія хвилі викривлюється в бік земної поверхні. Ефект викривлення траєкторії руху хвилі називається рефракцією. Необхідно встановити залежність радіуса викривлення траєкторії поширення радіохвилі r від швидкості зміни показника заломлення, тобто від градієнтів або . Розглянемо поведінку траєкторії хвилі при переході від i-го шару із показником заломлення n до (i+1)-го шару з показником n+dn (рис. 2.5, б).

Промінь, який падає на нижню межу (i+1)-го шару, виявляється повернутим відносно променя, що падає на i-й шар, на кут dq, рівний куту, який створюється дотичними до точок A_i і A_i+1. Цей кут дорівнює центральному куту з вершиною в точці О.

а)

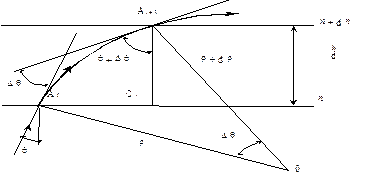
б)

Рис. 2.5

Шуканий радіус кривизни r траєкторії радіохвилі визначається відрізком „прямої ” A_i A_i+1 й кутом dq за такою формулою:

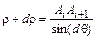. (2.13)

В реальних умовах переважна більшість трас поширення радіо-хвиль характеризується нехтовно малими значеннями кута dq.

Враховуючи малу величину кута dq й нерівність 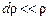, співвідношення (2.13) запишемо у вигляді:

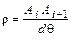. (2.14)

Через гіпотенузу трикутника A_i A_i+1C_i знаходимо, що

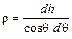. (2.15)

На підставі другого закону Снелліуса запишемо:

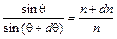. (2.16)

Із співвідношення (2.16) після простих тригонометричних перетворень, нехтуючи складовими другого порядку малості, знаходимо

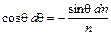. (2.17)

Підставляючи отримані значення в рівність (2.17), визначаємо

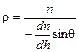. (2.18)

Для тропосфери без видимого погіршення точності розрахунків, можна вважати, що 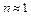. У цьому випадку співвідношення (2.18) набуває вигляду

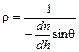. (2.19)

При поширенні земних хвиль кут q наближається до 90^о. При цьому співвідношення (2.19) спрощується:

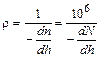. (2.20)

Із співвідношень (2.19) і (2.20) видно, що в приземному шарі атмосфери радіус скривлення променя залежить не від абсолютного значення n, а від його градієнта.