Многоэлектронные системы.

Диаграммы состояния определяют фазовый состав и структуру сплавов в условиях равновесия, дают возможность решать вопросы их упрочнения путем термической обработки и поэтому являются основой классификации сплавов цветных металлов. По технологическим свойствам сплавы делят на деформируемые, находящиеся в состоянии твердых растворов и хорошо обрабатываемые давлением, и литейные, имеющие в структуре эвтектику и обладающие наилучшей жидкотекучестыо. По способности упрочняться с помощью термической обработки цветные сплавы подразделяют на неупрочняемые и упрочняемые термической обработкой - закалкой без полиморфного превращения и старением.

Упрочняемыми термической обработкой являются сплавы, для которых характерно уменьшение растворимости компонентов в твердом состоянии при снижении температуры до нормальной (комнатной). В промышленности широкое применение находят как двойные, тройные, так и поликомпонентные сплавы цветных металлов, фазовый состав и структура которых в условиях равновесия определяются соответствующими диаграммами состояния. Несмотря на это, при небольшом содержании легирующих элементов в большинстве случаев вполне достаточным для качественного описания изменений фазового состава, структуры является ис-пользование наглядных двойных диаграмм состояния "цветной металл - основной легирующий элемент". В соответствии с подобной диаграммой "алюминий - легирующий элемент" (рис.1) сплавы с содержанием легирующего элемента до проекции точки В на ось концентраций являются деформируемыми, а с большим содержанием - литейными. При этом сплавы с содержанием легирующего элемента до точки D не упрочняются в, результате термической обработки, а сплавы с большим содержанием являются упрочняемыми термической обработкой. Наиболее широко распространены цветные сплавы на основе алюминия, меди, магния, олова.

Алюминиевые сплавы в соответствии с диаграммой состояния "алюминий - легирующий элемент"(см.рис.1) делят на деформируемые и литейные.

Промышленное применение находят как двойные деформируемые сплавы алюминия с медью, магнием, марганцем, кремнием, так и поликомпонентные сплавы систем Al-Cu-Mg (дуралюмины), Al-Cu-Si (авиали) и др. Значительное место среди этих сплавов занимают дуралюмины, маркируемые буквой Д и цифрами, характеризующими порядковый номер сплава по ГОСТ 4784-74, например, Д1, Д6, Д16.

Наиболее распространенный из них сплав марки Д1 содержит в качестве легирующих элементов 3,8-4,8%Сu; 0,4-0,8%Мg; 0,4-0,8%Мn. Дуралюмины относятся к сплавам, упрочняемым термической обработкой. К литейным относятся сплавы алюминия с кремнием, медью, магнием. Литейные сплавы маркируются буквами АЛ и цифрами, обозначающими порядковый номер сплава (ГОСТ 2685-75), например, АЛ2, АЛЗ. Наибольшее распространение получили силумины (сплавы алюминия с кремнием), содержащие от 5 до 13% Si.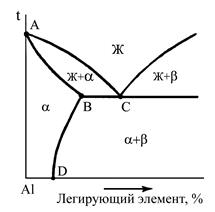

Рис.1. Фрагмент диаграммы состояния системы алюминий - легирующий элемент

Фазовый состав, структуру и свойства силуминов можно варьировать изменением химического состава, модифицированием - введением веществ, которые уже в малых количествах (обычно не более десятых долей процента) способствуют кристаллизации структурных составляющих в измельченной форме, а также термической обработкой. В качестве модифицирующих добавок используются марганец, никель, хром, титан, ванадий, и некоторые другие элементы. Силумины обычно модифицируют натрием, который в жидкий сплав вводят в виде смеси фтористых и хлористых солей натрия в соотношении 2/3NaF+1/3NаCl.

Важнейшими сплавами на основе меди являются латуни (сплавы меди с цинком) и бронзы (сплавы меди со всеми элементами, кроме цинка). По технологическим свойствам медные сплавы подразделяют на деформируемые и литейные, по способности упрочняться - на неупрочняемые и упрочняемые термической обработкой.

Двойные деформируемые латуни маркируются буквой Л и цифрой, показывающей среднее содержание меди в процентах (ГОСТ 15527-70), например, Л96, Л90, Л80, Л70, Л62, Л59. Латуни с содержанием меди 90% и более называются томпаком (например, сплав марки Л96), при 80-85% - полутомпаком (Л80). В марках легированных деформируемых латуней кроме цифры, показывающей содержание меди, указываются буквы и цифры, обозначающие легирующий элемент и его содержание в процентах. Например, сплав ЛАН59-3-2 содержит 59%Cu, 3%Al, 2%Ni, остальное Zn. В марках литейных латуней указывается содержание цинка, а содержание каждого легирующего элемента ставится непосредственно за буквой, его обозначающей. Например, сплав ЛЦ40Мц3А содержит 40%Zn, 3%Мn, 1%Al, остальное Cu.

Бронзы по основным легирующим элементам подразделяют на оловянистые, свинцовистые, кремнистые и др. В бронзах в качестве легирующей добавки в небольших количествах может присутствовать и цинк. Деформируемые бронзы маркируют буквами Бр, за которыми следуют буквы и цифры, обозначающие название и содержание в процентах легирующих элементов (ГОСТ 5017-74). Например, сплав БрОЦС4-4-2,5 содержит 4%Sn, 4%Zn, 2,5%Рb, остальное Сu. В марках литейных бронз (ГОСТ 613-73) содержание каждого легирующего элемента указывается сразу после буквы, обозначающей его название. Например, сплав БрО6Ц6С3 содержит 6%Sn, 6%Zn, 3%Рb, остальное Сu .

Магниевые сплавы, легирующими элементами которых являются алюминий, цинк, кремний, а также редкие металлы - неодим, торий и другие, подразделяются на деформируемые и литейные, маркируемые соответствующими буквами МА и МЛ и цифрами, соответствующими номеру сплава (ГОСТ 14957-76 и 2856-79). Магниевые сплавы, как деформируемые, так и литейные, подвергают модифицированию и упрочняющей термической обработке.

Сплавы на основе олова (оловянистые баббиты) являются высококачественными антифрикционными материалами, для которых важным является наличие гетерогенной (неоднородной) структуры, состоящей из мягкой, пластичной основы, обеспечивающей прирабатываемость подшипника к валу, и твердых включений, упрочняющих материалы и препятствующих схватыванию трущихся поверхностей. Оловянистые баббиты представляют собой трехкомпонентные сплавы системы олово-сурьма-медь. Наиболее широкое применение имеет сплав марки Б83 (ГОСТ 1320-74), содержащий 83%Pb, 11%Sb и 6%Cu.

2. МИКРОСТРУКТУРНЫЙ АНАЛИЗ ЦВЕТНЫХ СПЛАВОВ

Микроструктура цветных сплавов в условиях равновесия или близких к ним может быть определена с помощью их диаграмм состояния.

2.1. Микроструктура сплавов на основе алюминия

В качестве характерных представителей деформируемых и литейных алюминиевых сплавов в работе используются соответственно литой дуралюмин марки Д1 и силумин марки АЛ2.

Основу сплавов типа дуралюмин составляет система Al-Cu-Mg. В соответствии с ней медь и магний имеют ограниченную растворимость в твердом состояний в алюминии, а избыточными фазами, выделяющимися при охлаждении из a-твердого раствора меди и магния в алюминии в связи с уменьшением растворимости компонентов при снижении температуры являются соединения CuAl₃ и Al₂MgCu, называемые соответственно Q и S фазами. Поскольку магний в сплаве находится в небольшом количестве, то фаза S при используемых в работе увеличениях микроскопа в структуре не обнаруживается.

Поэтому наблюдаемая микроструктура сплава марки Д1 в литом состоянии состоит из светлых зерен a-твердого раствора меди и магния в алюминии и темных включений Q-фазы (соединения СuАl2), располагающихся по границам зерен a-фазы (рис.2). Такую структуру дуралюмина марки Д1 можно предсказать, исходя из двойной диаграммы состояния системы Al-Сu, подобной изображенной на рис.1. Дуралюмины, как и авиали (сплавы системы Al-Cu-Si) применяют для изготов-

Рис.2. Схема микроструктуры дуралюмина марки Д1 в литом состоянии. a-фаза и Q-фаза. ´340

ления горячей или холодной обработкой давлением листов, труб, проволоки, плит и различных профилей.

Микроструктура силуминов соответствует двойной диаграмме состояния системы Al-Si (рис.3), доэвтектические сплавы состоят из первичных кристаллов a-твердого раствора кремния в алюминии и зерен эвтектики (a+b). В свою очередь, структура заэвтектических сплавов состоит из крупных первичных кристаллов - твердого раствора алюминия в кремнии в виде игл и зерен эвтектики (a+b). В соответствии с диаграммой состояния Al-Si сплав марки АЛ2, содержащий 12-13%Si, является заэвтектическим.

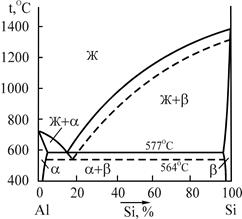
Рис.3. Диаграмма состояния системы алюминий – кремний

Поэтому его микроструктура состоит из более темных крупных игл b-твердого раствора алюминия в кремнии и эвтектики в виде более темных игл b-твердого раствора алюминия в кремнии на светлом поле a-твердого раствора кремния в алюминии (рис.4). Сплав в таком структурном состоянии обладает низким комплексом механических свойств (предел прочности при растяжении s_В=130-140МПа, относительное удлинение d=1-2%). Поэтому для повышения свойств производят модифицирование. Применительно к силуминам оно заключается в обработке перед разливкой сплава смесью фтористых и хлористых солей натрия в соотношении 2/3NaF+1/3NaCl. Это обеспечивает введение в сплав 0,1%Na, который осуществляет модифицирующее действие, затрудняя кристаллизацию b-твердого раствора алюминия в кремнии. Модифицирование вызывает смещение линий на диаграмме состояния Al-Si (см. рис.3). Эвтектическая точка (11,6%Si) перемещается вправо, приобретая концентрацию кремния 14,6%, в результате чего сплав становится доэвтектическим, что исключает из структуры крупные первичные иглы b-твердого раствора алюминия в кремнии и тем самым повышает пластичность. Линия эвтектического превращения снижается с 577 до 564^OС, в связи с чем эвтектика (a+b) вместо грубоигольчатой становится мелкозернистой. Поэтому микроструктура сплава марки АЛ2 после модифицирования состоит из светлых первичных зерен a-твердого раствора кремния в алюминии и мелкозернистой эвтектики в виде более темных включений b-твердого раствора алюминия в кремнии на светлом поле a-твердого раствора кремния в алюминии (рис.5). Силумины применяются для изготовления корпусов компрессоров, картеров и блоков цилиндров двигателей и др.

Рис.4. Схема микроструктуры силумина марки АЛ2 до модифицирования, b-фаза и эвтектика (a+b). ´250

Рис.5. Схема микроструктуры силумина марки АЛ2 после модифицирования. a-фаза и эвтектика (a+b). ´250

2.2. Микроструктура сплавов на основе меди

В качестве характерных представителей сплавов на медной основе в работе используются сплавы марок Л68 и Л59 (латуни) и БрО10 и БрС30 (бронзы).

Микроструктура двойных низколегированных латуней в условиях равновесия определяется диаграммой состояния системы Сu-Zn. На рис.6 приведен фрагмент этой диаграммы, отражающей фазовые равновесия в сплавах с содержанием цинка до 50%, (промышленное применение находят латуни, содержащие до 45%Zn). В соответствии с этой диаграммой состояния латуни по структуре делятся на однофазные (a-латуни), содержащие до 39%Zn и состоящие из зерен a-твердого раствора цинка в меди, и двухфазные (a+b)-латуни, содержащие от 39 до 45%Zn и состоящие из зерен a-твердого раствора цинка в меди и зерен b-твердого раствора на основе соединения CuZn.

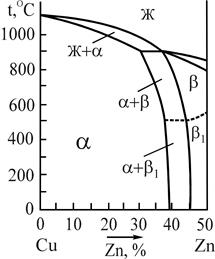Рис.6. Фрагмент диаграммы состояния системы медь-цинк

Однофазные a-латуни обладают высокой пластичностью при нормальной (комнатной) температуре. Поэтому однофазные латуни выпускают в виде полуфабрикатов, полученных холодной обработкой давлением (штамповкой, прокаткой или протяжкой) листов, труб, лент, проволоки, из которых методом глубокой вытяжки изготавливают радиаторные трубы, снарядные гильзы, сильфоны, трубопроводы, а также производят детали (шайбы, втулки, уплотнительные кольца), не требующие высокой твердости. Холодная обработка вызывает наклеп.

В наклепанном состоянии латунь с содержанием цинка 20% и выше подвержена растрескиванию по границам зерен, имеет низкую коррозионную стойкость.Поэтому ее подвергают рекристаллизационному отжигу, в результате чего однофазная латунь приобретает зеренную структуру с характерными для пластичных сплавов двойниками.

Рис.7. Схема микроструктуры однофазной латуни марки Л68 после холодной пластической деформации и рекристаллизационного отжига, a-фаза. ´440

Рис.8. Схема микроструктуры двухфазной латуни марки Л59 в литом состоянии. a-фаза и b-фаза. ´440

На рис.7 показана микроструктура однофазной латуни марки Л68. Поскольку зерна a-фазы выходят на поверхность микрошлифа различными кристаллографическими плоскостями, степень их травимости реактивом различна и они имеют неодинаковую окраску.Микроструктура двухфазной латуни марки Л59 в литом состоянии, представленная на рис.8, состоит из светлых зерен a-твердого раствора цинка в меди и темных (более богатых цинком и травящихся сильнее) зерен b-твердого раствора на базе химического соединения CuZn. Присутствие в структуре b- фазы, имеющей низкую пластичность и высокую твердость, повышает характеристики прочности латуней. Двухфазные латуни являются более пластичными при температурах выше 500^ОС. Поэтому эти латуни выпускают в виде полуфабрикатов, полученных горячей обработкой давлением, - листов, прутков, труб, штамповок, из которых изготавливают втулки, гайки, тройники, штуцеры, токопроводящие детали электрооборудования и др.

Легированные латуни применяют в качестве деформируемых и литейных. Последние, как правило, содержат большое количество цинка и легирующих элементов.

В промышленности находят применение как двойные – оловянные, свинцовистые и др. бронзы, так и многокомпонентные, содержащие кроме основных легирующих элементов добавки свинца, цинка, фосфора и никеля.

Микроструктура двойных оловянных бронз определяется диаграммой состояния системы Сu-Sn. На рис.9 приведен фрагмент этой диаграммы для сплавов с содержанием олова до 30%, (промышленное применение имеют сплавы, содержащие до 20%Sn). Сплошными линиями показаны границы фазовых областей равновесной системы.

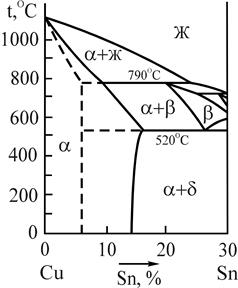Рис.9. Фрагмент диаграммы состояния системы медь-олово

Рис.10. Схема микроструктуры двухфазной бронзы марки БрО10 в литом состоянии. a-фаза и эвтектоид(a+d). ´600

В соответствии с этой диаграммой состояния бронзы по структуре делятся на однофазные, состоящие из зерен a-твердого раствора олова в меди, и двухфазные, состоящие из зерен a-твердого раствора олова в меди и зерен эвтектоида (a+d) , в котором d-фаза представляет собой соединение Cu₃₁Sn₈. При очень медленном охлаждении протекает равновесная кристаллизация и граница между однофазными и двухфазными бронзами соответствует 14% олова. В реальных заводских условиях при литье в металлические и земляные формы происходит ускоренное охлаждение сплавов, в связи с чем диффузия атомов олова в меди затрудняется и сплавы ведут себя так, как если бы растворимость олова в меди была постоянной, равной 6-8%, и не менялась с температурой (пунктирные линии на рис.9). Исходя из этого, однофазными являются бронзы с содержанием олова не более 5-6%. Такие сплавы имеют высокую пластичность и являются деформируемыми.

Бронзы, содержащие олово в большем количестве, по структуре являются двухфазными. Микроструктура двухфазной бронзы марки БрО10 состоит из темных зерен a-твердого раствора олова в меди и зерен эвтектоида (a+d) (рис.10). Основой эвтектоида является d-фasa (химическое соединение Сu₃₁Sn₈), на белом поле которой расположены мелкие темные выделения a-фазы. Наличие твердой и хрупкой d-фазы исключает возможность обработки давлением, поэтому такие бронзы применяют только в литом состоянии.

Для повышения свойств в оловянистые бронзы вводят различные добавки: цинк для улучшения жидкотекучести и повышения плотности отливок; фосфор как раскислитель для устранения нежелательной окиси олова SnO₂, присутствующей в бронзах в виде твердых и хрупких включений; свинец для улучшения обрабатываемости резанием и повышения уровня антифрикционных свойств. Оловянистые бронзы с перечисленными добавками находят в промышленности более широкое применение, чем двойные сплавы. В качестве примера можно назвать литейные бронзы марок БрО5Ц5С5, БрО10Ф1 и др., деформируемые бронзы марок БрОФ6,5-0,4, БрОЦ4-3 и др. Оловянистые бронзы используются для изготовления паровой и водяной арматуры, подшиников скольжения, втулок, зубчатых колес, деталей приборов.

Микроструктуру свинцовистых бронз можно охарактеризовать с помощью двойной диаграммы состояния системы Сu-Pb (рис.11). Как видно из диаграммы состояния, свинцовистая бронза марки БрС3О с содержанием свинца 30% является доэвтектическим сплавом и его структура при нормальной (комнатной) температуре должна состоять из зерен a-твердого раствора свинца в меди и эвтектики, состоящей из a-твердого раствора свинца в меди и b-твердого раствора.

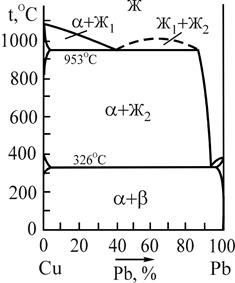Рис.11 Диаграмма состояния системы медь-свинец

Рис.12 Схема микрострукуры свинцовистой бронзы марки БрС3О в литом состоянии. a-фаза и эвтектика (a+b). ´340

Однако эвтектика по составу совпадает с чистым свинцом (99,98%), а a-фаза - с чистой медью, поэтому можно сказать, что фактически микроструктура сплава состоит из зерен двух металлов - свинца и меди.

На рис.12 представлена микроструктура свинцовистой бронзы марки БрС3О, состоящая из светлых зерен a-фазы (фактически меди) и темных зерен эвтектики (фактически свинца). Свинцовистые бронзы являются высококачественными антифрикционными материалами и применяются для изготовления опорных и шатунных подшипников мощных турбин, авиационных моторов, дизелей и других машин.

2.3 Микроструктура сплавов на основе магния

Микроструктура магниевых сплавов в равновесном состоянии определяется соответствующими диаграммами состояния. В качестве примера на рис.13 приведена микроструктура сплава МЛ5, содержащего помимо магния 8%Al; 0,8%Zn и 0,3%Мn. Алюминий и цинк введены в сплав для упрочнения, а марганец - для повышения коррозионной стойкости.

Рис.13 Схема микроструктуры сплава марки МЛ5 в литом состоянии, a-фаза и g-фазa (Mg4Al3). ´600

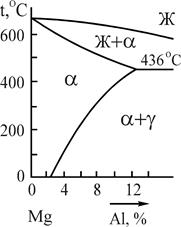Рис.14 Фрагмент диаграммы состояния системы магний - алюминий

Поскольку растворимость цинка в магнии в твердом состоянии составляет не менее 1,7% и, следовательно, все количество цинка входит в твердый раствор, не присутствуя в сплаве как самостоятельная структурная составляющая, а марганцовистая фаза при используемых в работе увеличениях ввиду малого ее количества не выявляется, то микроструктура сплава марки МЛ5 может быть определена в соответствии с двойной диаграммой состояния системы Mg-Al (рис.14).

Микроструктура сплава марки МЛ5 (см. рис.13) состоит из светлых зерен a-твердого раствора алюминия в магнии и более темных включений g-фазы (соединения Mg₄Al₃), располагающихся по границам зерен a-фазы.

Микроструктура сплавов на основе олова

Микроструктура сплавов на основе олова в равновесном состоянии также может быть определена с помощью соответствуощих диаграмм состояния, например, оловянистого баббита марки Б83 - с помощью тройной диаграммы состояния системы Sn-Sb-Cu. Микроструктура этого сплава в литом состоянии состоит из тройной эвтектики в виде основного темного поля a-твердого раствора сурьмы в олове и равномерно распределенных светлых мелких включений соединения SnSb и Cu₆Sn₅,

светлых крупных кристаллов соединения SnSb и светлых мелких кристаллов соединения Cu₆Sn₅ в виде игл или звездочек (рис.15).

Соединение Cu6Sn5 кристаллизуется в первую очередь и равномерно распределяется в объеме жидкости, образуя своеобразную сетку, препятствующую ликвации по удельному весу легких кристаллов SnSb. При этом вся медь, находящаяся в сплаве, расходуется на образование соединения SnSb. Мягкая, пластичная основа в виде тройной эвтектики и твердые включения соединений SnSb и Cu6Sn5 обеспечивают высокий уровень антифрикционных свойств и применяются для заливки подшипников газовых турбин, турбокомпрессоров, турбонасосов и др.

Рис.15. Схема микроструктуры баббита марки Б83 в литом состоянии. SnSb, Cu6Sn5 и тройная эвтектика (a+SnSb+Cu6Sn5). ´200

Многоэлектронные системы.

5.1. Общее описание многоэлектронной системы.

Формальное применение квантовой механики для описания многоэлектронных систем – атомов и молекул, не представляет трудностей. Для них можно построить гамильтониан и записать соответствующее уравнение Шрёдингера. Однако решение такого уравнения оказывается невозможным. Это связано с тем, что не существует такой системы координат, в которой можно было бы разделить переменные (координаты электронов) в многоэлектронном уравнении. Невозможность такого разделения связана с существованием электростатического взаимодействия между электронами, которым нельзя пренебречь. Поскольку решение уравнения Шрёдингера путём разделения переменных невозможно, были развиты различные подходы к описанию электронного строения атомов и молекул (адиабатическое приближение, одноэлектронное приближение и т.д.). Хотя это чисто математические приёмы, однако именно они позволили сформировать понятийный аппарат современной квантовой химии. В общем случае под многоэлектронной системой понимают систему, состоящую из 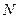электронов и 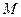ядер. Если 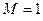, то рассматриваемая система будет представлять собой многоэлектронный атом. Если же 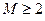, то система является молекулярной (молекула, радикал, ион). В связи с этим для многоэлектронной системы, при условии что 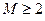, можно использовать общий термин - молекулярная система. Полная волновая функция молекулярной системы зависит от пространственных (орбитальных) и спиновых координат электронов, а также от пространственных координат ядер:

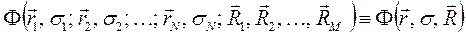
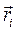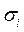здесь и - пространственные и спиновые координаты электронов; 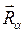- координаты ядер рассматриваемой многоэлектронной системы. Как и во всех других случаях, гамильтониан молекулярной системы 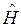записывается по образцу классического 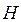и включает в себя операторы двух типов – кинетической 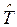и потенциальной 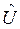энергии. Как известно, кинетическая энергия – аддитивная величина, она равна сумме кинетической энергии ядер и электронов . Потенциальную энергию системы заряженных частиц можно записать как сумму трёх слагаемых: потенциальной энергии притяжения электронов к ядрам, ; потенциальной энергии межэлектронного отталкивания, 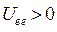и потенциальной энергии межъядерного отталкивания, 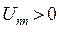. Тогда оператор Гамильтона для молекулярной системы как совокупность соответствующих операторов, будет иметь следующую структуру:

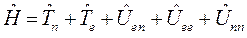
Как известно, масса ядра намного больше массы электронов. В силу этого, период ядерных колебаний на несколько порядков превышает период электронных колебаний. В связи с этим молекулу можно рассматривать состоящей из двух подсистем: медленной (ядерной) и электронной (быстро меняющейся) подсистем. Медленно движущаяся система ядер образует электростатическое поле, в котором с намного большей скоростью движутся электроны. Различие скоростей движения этих подсистем настолько велико, что электроны практически мгновенно реагируют на изменения в положении ядер в пространстве, успевая «подстроиться» к этому изменению. В 1927 г. М. Борн и Р. Оппенгеймер предложили упрощённый подход, в рамках которого электронное движение полностью отделяют от движения ядер. В адиабатическом приближении также рассматривают отдельно электронные и ядерные движения, однако учитывают их слабое взаимодействие. В квантовой механике адиабатическое приближение определяет уравнения, которые описывают движение электронов (точнее говоря, их состояния) при фиксированных значениях ядерных координат. Действительно, если принять массу ядер бесконечно большой, их скорости становятся равными нулю, а это значит, что будет равна нулю и их кинетическая энергия 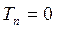. Таким образом, в адиабатическом приближении движения электронов и ядер считают независимыми, полагая ядра жёстко фиксированными. Тогда волновая функция 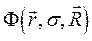может быть записана в виде произведения электронной 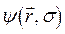и ядерной (или колебательной) 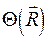функций:

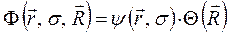
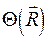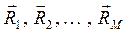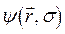здесь представляет собой ядерную функцию, которая зависит только от координат ядер ; а - электронная функция, зависящая от координат электронов 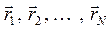. Необходимо заметить, что координаты ядер входят в электронную функцию как фиксированные параметры, это означает, в свою очередь, что 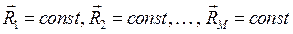. На основании приведенных выше выкладок, несложно записать уравнение Шрёдингера для молекулярной системы в операторном виде:

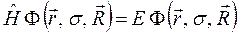
где 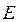- полная энергия молекулярной системы. В адиабатическом приближении данное уравнение распадается соответственно на два уравнения вида: уравнение движения электронов в поле фиксированных ядер (электронное уравнение) и уравнение движения ядер (ядерное уравнение). В квантовой химии решают электронное уравнение:

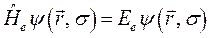
здесь:

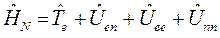
Таким образом, гамильтониан многоэлектронной системы при фиксированном положении ядер можно рассматривать состоящим соответственно из вклада кинетической энергии всех 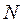электронов, электростатического притяжения каждого 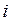-го электрона ко всем 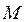ядрам с зарядами 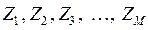и координатами 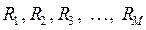, электростатического отталкивания электронов, а также кулоновское отталкивание ядер. Последнее впрочем не повлияет на решение электронной задачи, но должно учитываться в более точных расчётах, т.е. имеем:

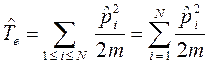
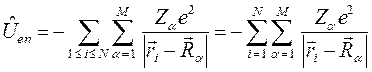
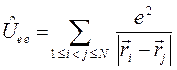
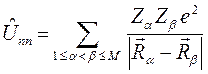
Ядерное (или колебательное) уравнение служит основой задач о колебаниях и вращениях молекул (ИК - спектроскопия, спектры КР и т.д.):

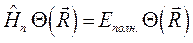
здесь:

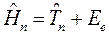
Полная энергия молекулярной системы, очевидно, будет представлять собой сумму электронной энергии, вычисленную при фиксированном расположении ядер в пространстве, и ядерной составляющей :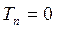

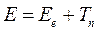
В адиабатическом приближении электронная энергия 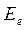зависит от взаимного расположения ядер, причём эта же энергия как функция координат ядер 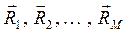может быть интерпретирована как потенциальная энергия электронов в поле ядер, 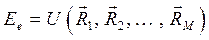. В системе координат 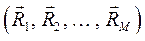функции 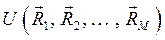соответствует некоторая поверхность, которую называют поверхностью потенциальной энергии (ППЭ). Приближение Борна-Оппенгеймера и адиабатическое приближение теряют смысл для вырожденных или квазивырожденных электронных состояний. В случае вырождения, электронные уровни смешиваются с колебательными и вращательными уровнями. Такие состояния называют также ровибронными. Для молекулярной системы, состоящей из 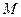ядер и 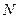электронов, введём обозначения, которых будем придерживаться в последующих выкладках: 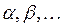- номера ядер в молекулярной системе; 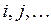- номера электронов. Тогда одноэлектронный гамильтониан для электрона с номером 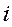включающий в себя оператор кинетической энергии и оператор потенциальной энергии притяжения электрона ко всем ядрам системы 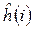и оператор межэлектронного взаимодействия, двухэлектронный оператор 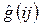– отталкивания двух электронов 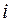и 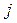могут быть записаны в виде:

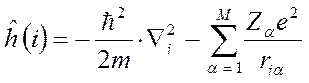
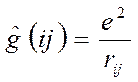
С учётом выражений полученных выше, выражение для электронного гамильтониана молекулярной системы можно представить в виде:

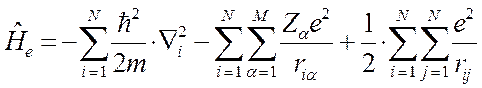
или в более компактной форме:

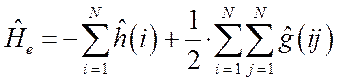
В полученном нами выше выражении символ двойной суммы, в общем случае означает, что суммирование проводится по всем электронам и, следовательно, сумма состоит из слагаемых:

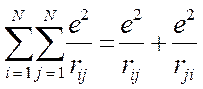
а также учитывая, что:

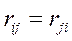
то каждое взаимодействие в такой сумме учтено дважды. При этом правая и левая части соотношения не равны друг другу, т.к. здесь каждое взаимодействие учтено дважды:

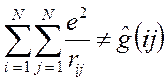
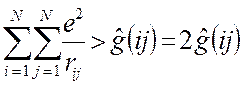
Для того чтобы учесть каждое взаимодействие один раз, перед выражением для потенциальной энергии ставят множитель 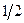, т.е. имеем:

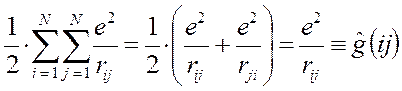
Электронный гамильтониан молекулярной системы всегда содержит слагаемое, отвечающее отталкиванию ядер. Поскольку в адиабатическом приближении расстояния между ядрами строго фиксированы, это слагаемое входит в гамильтониан как параметр и для простоты изложения обычно не учитывается, однако при точных количественных расчётах этот учёт необходим.

5.2. Волновая функция многоэлектронной системы.

Тождественность частиц. Принцип Паули.

В связи с тем, что мы имеем дело с многоэлектронными системами (атомами, молекулами, комплексами и т.д.), возникает вопрос о структуре и свойствах многоэлектронной волновой функции. В квантовой механике он решается на основе двух важнейших принципов – принципа тождественности частиц и принципа Паули. В системе одинаковых (тождественных) частиц реализуются только такие состояния, при которых наблюдаемые физические характеристики системы не изменяются при обмене частиц координатами. В справедливости данного принципа не трудно убедиться. Действительно, пусть у нас имеется некоторая двухэлектронная система. Полную волновую функцию такой системы обозначим, как 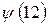и будем называть её двухэлектронной волновой функцией. Здесь символ 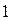соответствует совокупности всех координат (пространственных и спиновых) первой частицы, а символ 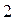- совокупности всех координат второй частицы. В силу принципа тождественности перестановка частиц местами не должна сказаться на значениях наблюдаемых физических величин. Математически такая перестановка соответствует обмену частиц местами, т.е. переходу от функции 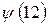к функции 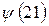. Если эти функции являются собственными функциями гамильтониана, то они должны соответствовать одному и тому же собственному значению полной энергии системы :

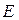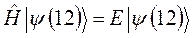
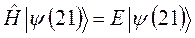
При этом средние значения для оператора 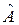, вычисленные с функциям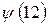и и 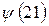, также должны совпадать:

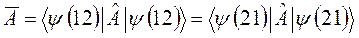
Симметричные волновые функции при перестановке координат двух частиц местами не меняют знак, а антисимметричные – меняют. Очевидно, что свойствами:

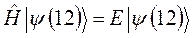
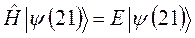
обладают как симметричные, так и антисимметричные волновые функции. Это означает, в свою очередь, что:

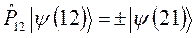
здесь 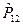- оператор перестановки координат двух электронов. Симметричным волновым функциям соответствует знак плюс, а антисимметричным – знак минус. Из свойств симметрии волновых функций следует принцип Паули: «Волновая функция электронной системы должна быть антисимметричной относительно перестановки любой пары частиц местами». Это в свою очередь означает, что в квантовом состоянии, определяемом с помощью четырёх квантовых чисел , , 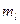и 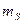, может находиться не более одного электрона. Данный принцип следует из требования антисимметрии электронной волновой функции. Следствием принципа Паули является так называемый запрет Паули, согласно которому, на одной атомной орбитали могут находиться не более чем два электрона, с противоположно направленными спинами (т.е. имеющими различные значения спиновых квантовых чисел). В соответствии с принципом Паули для двухэлектронной системы, выражение вида:

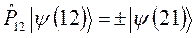
должно быть записано в виде:

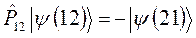
Необходимо отметить, что принцип Паули является важнейшим принципом квантовой механики. Он не является следствием основных её законов, а является утверждением, обобщающим экспериментальные факты. Это означает, что электронных систем, которые были бы симметричны по отношению к перестановке электронов местами, просто не существует. Для того чтобы принцип Паули соблюдался, частицы должны обладать полуцелым спином. К таким частицам, обладающим полуцелым спином и подчиняющимся принципу Паули – относятся фермионы, для которых справедливо распределение Ферми-Дирака. Фермионы находятся только в антисимметричных состояниях. К ним относятся электроны, а также ядра с нечётным числом частиц. Другой класс тождественных частиц – бозоны. К ним относятся 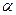– частицы, ядра с чётным числом частиц, атом водорода, атом гелия и т.д. Такие частицы обладают целочисленным (в том числе и нулевым) спином, а их волновые функции являются симметричными относительно перестановки координат двух частиц. Для бозонов справедлива другая статистика – Бозе-Эйнштейна, описываемая функцией. Поскольку согласно принципу Паули в каждом квантовом состоянии может находиться не более одного электрона, и если имеется система, состоящая из двух электронов, то возникает вопрос относительно вида волновой функции 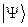, описывающей её состояние. Предположим, что состояние каждого из электронов задаётся своей волновой функцией 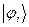, зависящей от пространственных 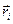и спиновых 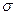координат, т.е.

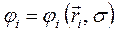
Обозначим всю совокупность пространственных и спиновых координат каждого из электронов соответственно символам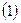и и 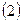. На основании теоремы о невзаимодействии, согласно которой «если система состоит из двух или нескольких невзаимодействующих подсистем, то её полная волновая функция 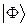равна произведению волновых функций отдельных подсистем 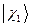, , 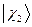, 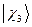…, , 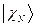а энергия – сумме энергий подсистем , , , …, »:

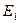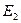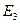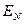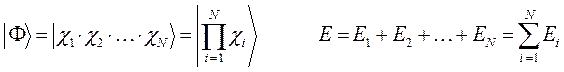
или для нашего случая:

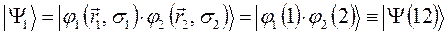
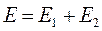
Поскольку все электроны тождественны и неразличимы, то обмен двух электронов местами не повлияет на энергию системы. Следовательно, в том же энергетическом состоянии рассматриваемую систему, состоящую из двух электронов можно описать функцией, образованной из 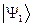перестановкой координат электронов. Для этого подействуем на исходную функцию 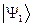оператором перестановки координат соответствующих электронов 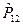, получим:

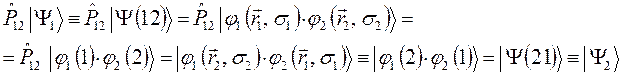
Итак, одному и тому же энергетическому состоянию отвечают две функци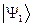и и 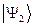, различающиеся между собой перестановкой координат. Каждая из них представляет собой частные, линейно независимые решения волнового уравнения Шрёдингера. Для того чтобы электронная волновая функция удовлетворяла принципу Паули, необходимо выполнение условия, согласно которому:

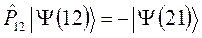
тогда соответственно из двух общих решений:

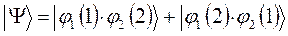
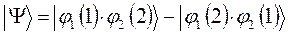
являющихся линейной комбинацией соответствующих частных решений:

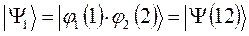
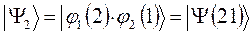
выбираем единственно возможное, построенное в соответствии с принципом антисимметрии:

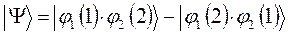
Решение со знаком «+» является симметричным по отношению к перестановке координат электронов ( 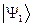при этом не меняет знака). Второе решение со знаком «-» называют антисимметричным (при перестановке координат функция 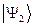меняет свой знак на противоположный), в чём достаточно легко убедиться. Для этого переставим координаты в соответствующих выражениях для :

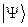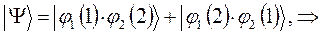
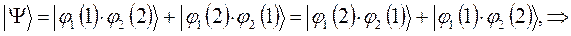
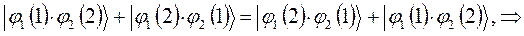
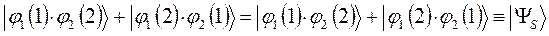
как это очевидно, волновая функция характеризующая состояние электронной системы не изменила свой знак. Такое решение, очевидно, будет являться симметричным относительно перестановки координат. Обозначим данное симметричное состояние 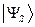. Аналогично проведём перестановку координат для решения вида:

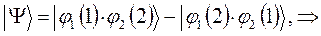
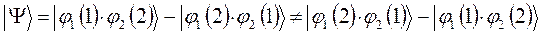
в данном случае приходим к неравенству вида:

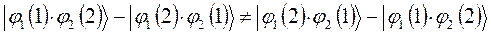
Очевидно, для того чтобы в ходе перестановки координат правая часть данного выражения была равна левой его части, необходимо полученное в ходе перестановки координат выражение заключить в скобки (сгруппировать) и полученный результат умножить на 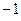. Выполнив над полученным тождествли соответствующие операции – сгруппировав соответствующие координаты, заключая последние в скобки, умножив полученный результат на 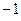, будем иметь:

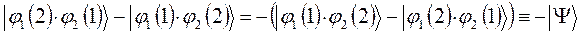
и таким образом:

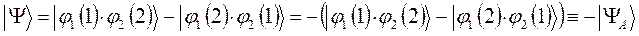
здесь симметричное ( 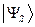) и ассиметричное ( 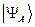) решения. Поскольку во втором случае волновая функция 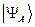меняет свой знак на противоположный, она является антисимметричной относительно операции перестановки координат 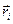. Какое из двух решени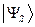й или 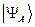отвечает реальной системе? Принцип Паули говорит, что системы, составленные из электронов, описываются исключительно антисимметричными полными волновыми функциями – частица может находиться в каком-либо одном из квантовых состояний. Нахождение двух частиц в одном и том же квантовом состоянии, очевидно, противоречит принципу Паули. Подтверждением справедливости данного принципа служит требование ортогональности волновых функций, согласно которому нахождение двух частиц в одинаковых квантовых состояниях равно нулю. Таким образом, с учётом принципа Паули, следует пользоваться выражением вида:

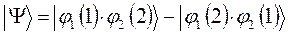
которое может быть записано в виде детерминанта второго порядка:

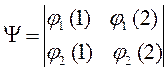
Обобщим теперь задачу построения антисимметричных волновых функций на случай системы из 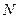невзаимодействующих электронов. Для этого запишем начальную многоэлектронную функцию в виде произведения одноэлектронных функций:

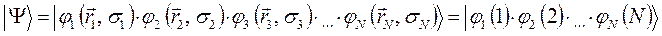
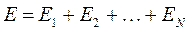
Тогда детерминант, формирующий антисимметричную 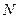- электронную волновую функцию, следует записать в виде:

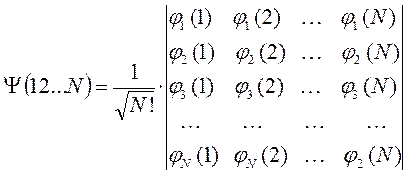
здесь нормировочный множитель 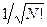- числовой коэффициент, гарантирующий нормировку многоэлектронной волновой функции 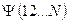на единицу:

Дж. Слейтер показал, что единственно возможно формой построения полностью антисимметричной волновой функцией 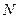- электронной системы из волновых функций отдельных независимых электронов является детерминант 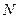- го порядка, который называют детерминантом (определителем) Слейтера, а волновую функцию, записанную в виде детерминанта Слейтера, называют детерминантной. Исходя из свойств определителей, можно показать справедливость принципа Паули, а также нормированность и ортогональность комбинируемых волновых функций. Предположим, что электроны в какой-то момент времени могут оказаться в одном и том же квантовом состоянии, т.е. что 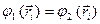, где 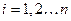. В теории матриц строго доказывается, что если две строки детерминанта 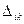оказываются одинаковыми, то в этом случае детерминант 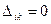. Полная волновая функция всегда отлична от нуля, т.к. в случае 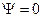вероятность найти электрон в элементе объёма 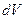также равна нулю. Поскольку это противоречит требованию нормировки, согласно которому вероятность нахождения электрона в элементе объёма равна единице, поэтому детерминант не может быть равен нулю:

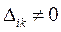
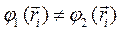
Так, если мы имеем систему невзаимодействующих электронов, то полную энергию такой электронной системы можно представить как сумму энергий отдельных частиц. Действительно, при отсутствии взаимодействия электронов в таких системах, двухэлектронные компоненты гамильтониана 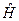будут равны нулю, т.е. 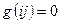и гамильтониан, таким образом, может быть записан в виде суммы отдельных одноэлектронных операторов 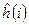. На основании теоремы о невзаимодействии, согласно которой «если система состоит из двух или нескольких невзаимодействующих подсистем, то её полная волновая функция 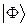равна произведению волновых функций отдельных подсистем 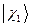, , 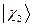, 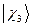…, , 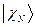а энергия – сумме энергий подсистем , , , …, ».

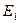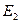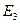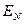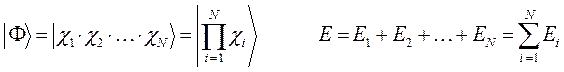
имеем соответственно:

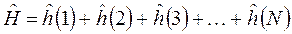
тогда 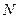- электронное уравнение Шрёдингера:

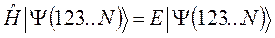
распадается на 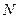- одноэлектронных уравнений вида:

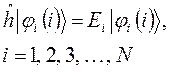
Полная энергия такой системы, при отсутствии межэлектронного взаимодействия, может быть записана в виде суммы:

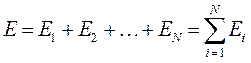
В силу тождественности электронов операторы 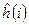одинаковы для разных 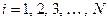и таким образом, задача о движении 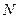невзаимодействующих частиц сводится к задаче о движении одной частицы, которая может быть решена точно. Формально адиабатическое приближение также является следствием независимости электронных и ядерных движений. В отличие от рассмотренных ранее идеализированных моделей, в реальных многоэлектронных системах (атомах, молекулах, ионах, комплексах и т.д.) существует значительное межэлектронное отталкивание, такие системы ещё называют сильно коррелированными. Однако и в этом случае используется модель детерминантной многоэлектронной функции, построенной на одноэлектронных функциях:

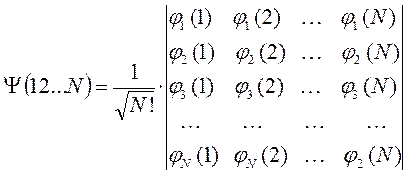
Действительно, каждому электрону в многоэлектронной системе можно приписать свою индивидуальную волновую функцию (орбиталь) 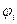. Это в свою очередь означает, что на каждый отдельный электрон действует единый усреднённый потенциал, создаваемый остальными электронами и ядрами. При этом полная волновая функция системы может быть представлена в виде произведения одноэлектронных функций, которые называют атомными орбиталями в случае атома и молекулярными орбиталями в случае молекулы. Такое приближение к точной многоэлектронной функции называют одноэлектронным (орбитальным) приближением или моделью независимых электронов. Итак, как это было показано уже выше, выражение для электронного гамильтониана молекулярной системы имеет вид:

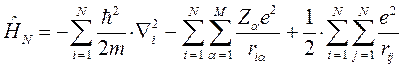
Электронный гамильтониан, очевидно, будет действовать только на пространственные функции и не будет зависеть от спиновых координат. Операторы квадрата спинового углового момента 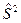и его проекции 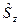, напротив, действует только на спиновую переменную 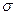. В связи с этим, одноэлектронную волновую функцию 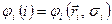в хорошем приближении можно представить в виде произведения пространственной 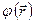и спиновой 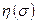волновых функций:

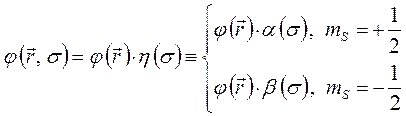
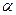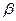здесь и соответствуют двум возможным проекциям спинового магнитного момента на ось .

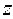при этом:

Такую одноэлектронную волновую функцию называют спин-орбиталью. Спин-орбиталь описывает пространственные и спиновые состояния одного электрона. Если же речь идёт о двух электронах, то в силу принципа Паули их полная волновая функция должна быть антисимметрична. На языке спин-орбиталей это означает, что если пространственные волновые функции двух электронов 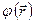совпадают, то спиновые компоненты 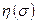должны отличаться:

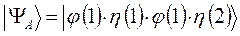
в противном случае мы будем иметь дело с простейшей симметричной двухэлектронной функцией, которую невозможно антисимметризовать, поскольку соответствующий ей детерминант Слейтера будет равен нулю. Действительно, представляя волновую функцию как некоторый вектор состояние вида:

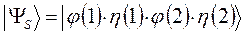
имеем соответственно:

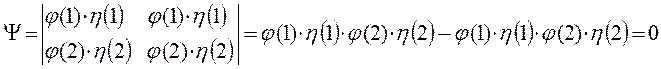
Следовательно, два электрона могут описываться одной пространственной волновой функцией, но при этом их спиновые состояния должны отличаться. И наоборот, если спиновые состояния двух электронов одинаковы, то должны отличаться их пространственные состояния. Это утверждение является следствием принципа Паули для модели независимых электронов. В случае многоэлектронного атома каждая спин-орбиталь характеризуется четырьмя квантовыми числам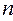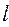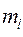и: , , и 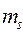. Причём пространственная волновая функция зависит от трёх квантовых чисел 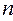, 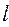и 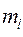, а спиновая – от одного 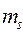. Учитывая это обстоятельство, принцип Паули можно сформулировать следующим образом: «Не может быть двух электронов с одинаковым набором четырёх квантовых чисел». Два электрона, занимающие одно пространственное состояние 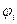и отличающиеся только спиновыми функциями, называют спаренными, а их спин-орбитали записывают в виде:

Система, состоящая только из спаренных электронов, называется системой с замкнутой оболочкой ( 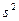, , 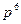, 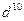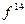и т.д.). Такая система содержит чётное число электронов, и она может быть описана одной детерминантной волновой функцией. В системах с открытой оболочкой (такие оболочки могут быть как чётно-электронными, так и нечётно-электронными) имеются пространственные состояния (орбитали), которые заняты одним электроном. При этом волновая функция таких систем может быть представлена линейной комбинацией двух или большего числа детерминантов Слейтера. На примере атомов нескольких химических элементов с открытыми и закрытыми оболочками, рассмотрим алгоритм построения такого рода детерминантных функций. Из соображений удобства изложения материала, рассмотрим каким образом можно построить детерминант Слейтера для многоэлектронных систем с замкнутыми оболочками. Как уже говорилось выше, к таким атомам относят системы, состоящие только из спаренных электронов. Такие системы содержат чётное число электронов и могут быть описаны только одной детерминантной волновой функцией. Рассмотрим метод построения такой функции на примере атома бериллия. Построение детерминанта Слейтера для заданной электронной конфигурации атома следует начинать с перечисления всех спин-орбиталей. Так, для основного состояния атома бериллия Be с электронной конфигурацией 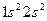, возможен следующий набор спин-орбиталей:

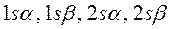
Затем следует записать первую строку детерминанта, указав в круглых скобках, что спин-орбитали относятся к первому электрону. Вторая и последующие строки детерминанта будут отличны друг от друга только номером электрона. В нашем случае имеем детерминант 4-го порядка. Таким образом, порядок детерминанта определяется числом электронов в рассматриваемой многоэлектронной системе. Итак, для атома бериллия имеем соответственно детерминант 4-го порядка:

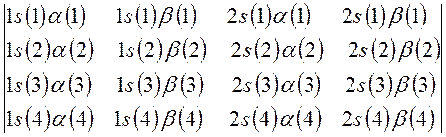
Далее перед детерминантом записывают нормировочный множитель 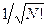- числовой коэффициент, гарантирующий нормировку многоэлектронной волновой функции 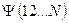на единицу:

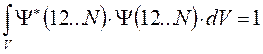
С учётом изложенных выше соображений, несложно записать детерминантную волновую функцию для атома бериллия – многоэлектронной системы с замкнутой оболочкой 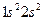, в виде:

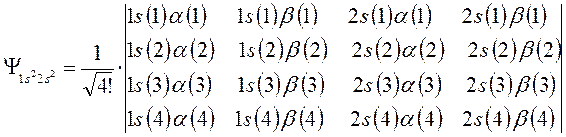
Рассмотрим теперь метод построения