Экспериментальные результаты
В работе были проведены измерения вязкости тонких (D = 30 ¸ 50 мкм) прослоек индивидуальных органических жидкостей и углеводородных технических смесей, образованных между металлическими пластинами. В случае ламинарного потока средняя скорость <vп> течения ньютоновской жидкости через щелевой зазор толщиной D (рисунок 34.3) определяется формулой:
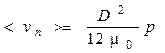 , (34.8)
, (34.8)
где p = DP/l (Па/м) – градиент давления по длине зазора l;
m0 (Па·с) – величина коэффициента вязкости жидкости.
Существование на боковых поверхностях щелевого зазора пристенного слоя с иными реологическими характеристиками, чем объемная жидкость, было установлено в опытах с описанным вискозиметром при анализе характера возрастания скорости течения жидкости <vэ> с повышением перепада давления, и сравнением таких зависимостей с теоретическими, рассчитываемыми по (34.7). Для исследуемых жидкостей при зазорах заведомо больших чем 2ds, т.е. в отсутствие перекрытия пристенных слоев, в области малых перепадов давления наблюдается уменьшение вязкости с ростом давления и поэтому нелинейное возрастание скорости течения жидкости, а при давлениях (0.5 ¸ 1) 104 Па вязкость становится равной вязкости объемной жидкости.
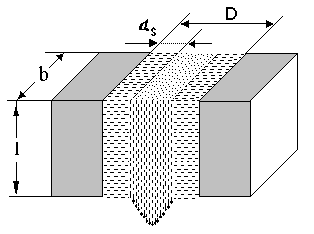 |
Рисунок 34.3 - Геометрия щелевого зазора вискозиметра и схема течения в нем жидкости с приповерхностным «жестким» слоем
Как пример, приведёны результаты (рисунок 34.4) опытов с технической углеводородной жидкостью МРХ-30. Для тонких (D ~ 30 ¸ 40 мкм) прослоек этого масла при небольшой скорости течения зависимость (34.7) не выполняется
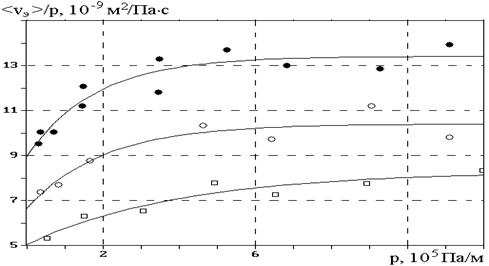
Рисунок 34.4 - Зависимость отношения <vэ> / p – относительной (по отношению к градиенту давления p) экспериментальной средней скорости течения масла МРХ-30 через щелевые зазоры вискозиметра от градиента давления p. Величина зазоров: D1 = 39,7 мкм (·), D2 = 35 мкм (О) и D3 = 30 мкм (обозн. – прямоугольник). Т = 294 К. Сплошные линии – аппроксимация зависимостью (34.9)
– величина <vэ> возрастает не пропорционально градиенту давления p. Экспериментальные результаты трех серий вискозиметрических опытов (при температуре Т = 294 К) с истечением этой жидкости через зазоры трех фиксированных толщин (D1 = 39,7 мкм, D2 = 35 мкм и D3 = 30 мкм) представлены на рисунке 34.4 в виде зависимости относительной (по отношению к градиенту давления p) скорости течения – величины (<vэ> /p, м2/Па×с) от p.
Экспериментальные данные аппроксимированы (сплошная линия) функцией:
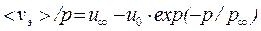 , (34.9)
, (34.9)
где u¥, u0 и p¥ – параметры аппроксимирующей зависимости (приведены в таблице 34.1).
Таблица 34.1 - Параметры аппроксимации (34.9) экспериментальной зависимости относительной (по отношению к градиенту давления p) средней скорости <vэ> /p = f(p) течения масла МРХ-30 от градиента давления p в щелевых зазорах вискозиметра трех фиксированных толщин D. Т = 294 К.
| Толщина зазора D, мкм | Параметры аппроксимации | ||
| u¥,×10–9, м2/Па×с | u0 ×10–9, м2/Па×с | p¥ ×105, Па/м | |
| 39,7 | 13,4 | 4,41 | 1,81 |
| 10,4 | 3,74 | 2,02 | |
| 8,3 | 3,24 | 4,04 |
Из рисунка 34.4 видно, что в области малых градиентов давления
p < 0,5 МПа/м величина отношения <vэ>/p с увеличением давления растет и лишь при градиентах (p > 0,5 МПа/м) c повышением давления практически не изменяется. При этом экспериментальная скорость истечения жидкости <vэ> меньше расчетной <vп>, а при больших перепадах давления становится равной ей.
1.2.3 Обсуждение результатов и модель «жесткого, срезаемого» пристенного слоя.
Наблюдаемый характер зависимости <vэ>/p = f(p) объясняется существованием в прослойке пристенных слоев толщиной 2ds. Их наличие приводит к тому, что реальное проходное сечение зазора s, по которому протекает жидкость, меньше, чем геометрическое S = bD (рисунок 34.3). С ростом приложенного давления и соответственно скорости течения равновесная толщина слоя на каждой из подложек уменьшается и, начиная с какого–то значительного перепада давления, проходное сечение зазора совпадает с геометрическим.
Поэтому для расчета параметров слоя рассмотрим его простейшую реологическую модель: на поверхностях обеих пластин, ограничивающих зазор, существует неподвижный (гидродинамически «жесткий») слой, периферийная часть которого «срезается» течением (рисунок 34.3). При постепенном увеличении скорости течения (за счет повышения перепада давления DP) толщина пристенного слоя убывает вплоть до нуля.
В такой модели, в соответствии с (34.8), рассматриваемая величина отношения <vэ>/p может быть представлена в виде:
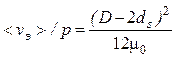 , (34.10)
, (34.10)
что позволяет по полученным экспериментальным зависимостям <vэ>/p = f(p) рассчитать как начальную толщину слоя d0s (ее значение при p = 0), так и ее текущее значение – величину ds в функции градиента давления или возрастающей с ним скорости течения жидкости <vэ>.
Рассчитанные таким образом значения толщины ds «жесткого, срезаемого» слоя в зависимости от средней линейной скорости <vэ> течения жидкости в данном зазоре для каждой из трех серий экспериментов приведены на рис.5. В принятой модели пристенного слоя для количественного описания явления его «срезания» течением зависимость ds = f(<vэ>) аппроксимировалась функцией:
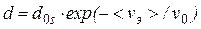 . (34.11)
. (34.11)
Здесь d0s (мкм) – толщина пристенного слоя при отсутствии течения, (<vэ>) – средняя (по сечению зазора) линейная скорость течения жидкости, v0 (мм/с) – параметр, характеризующий «жесткость» слоя, его способность к «срезанию» течением. Значения параметров d0s и v0 аппроксимирующей зависимости (34.11) приведены в таблице 34.2.
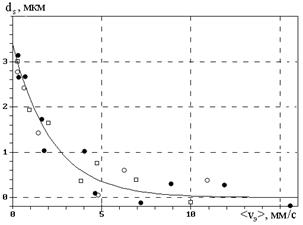 Рисунок 34.5 - Зависимость толщины пристенного слоя ds масла МРХ-30
(Т = 394 К) на стальной подложке в модели «жесткого, срезаемого течением слоя» от средней (по сечению) линейной скорости течения жидкости <vэ> в зазоре. Обозначения те же, что и на рисунке 34.4. Сплошная линия – аппроксимация D1 = 39,7 мкм (·) функцией (34.9)
Рисунок 34.5 - Зависимость толщины пристенного слоя ds масла МРХ-30
(Т = 394 К) на стальной подложке в модели «жесткого, срезаемого течением слоя» от средней (по сечению) линейной скорости течения жидкости <vэ> в зазоре. Обозначения те же, что и на рисунке 34.4. Сплошная линия – аппроксимация D1 = 39,7 мкм (·) функцией (34.9)
|
Таблица 34.2
| Параметры МОДЕЛИ | Толщина зазора D, мкм | ||
| 39,7 | 35,0 | 31,0 | |
| d0s, мкм | 3,4 | 3,2 | 3,1 |
| V0, мм/с | 2,2 | 1,9 | 2,6 |
Реологические характеристики пристенного слоя масла МРХ-30 (Т = 294 К) на поверхности стали в модели гидродинамически «жесткого, срезаемого слоя»
Как следует из рисунка 34.5 и таблицы 34.2, при отсутствии течения пристенный слой масла МРХ-30 на стальной подложке имеет толщину d0s » 3 мкм. «Прочность» слоя на «срезание» сравнительно невелика – уже при скоростях течения <vэ> = v0 ~ 2 мм/с толщина слоя ds~ 1 мкм, а при <vэ> ~ 10 мм/с ничтожно мала. Рассчитанная величина d0s близка, но несколько меньше значений равновесной толщины ЭЖК слоя (d0s » 7 ¸ 9 мкм) алифатических углеводородов и масел, полученных в оптических измерениях [2].
Расхождение с результатами таких измерений по толщине d0s можно объяснить несовершенством модели слоя, принятой для расчетов этого его параметра. В частности, не в пользу модели гидродинамически неподвижного слоя, о его «не жесткости» свидетельствует то, что даже при наименьших зазорах в наших измерениях не было отмечено предельного напряжения сдвига.
По-видимому, модель ЭЖК слоя, участвующего в течении жидкости, более адекватно может описать его реологические свойства. Для развития такой модели представляется необходимым одновременно с вискозиметрическим опытом проведение независимого измерения (оптическими или иными способами) структурных характеристик (толщины, однородности и др.) ЭЖК слоя прослойки при ее течении.
Дата добавления: 2015-01-13; просмотров: 1036;
