Нормирование отклонений и допусков формы цилиндрических поверхностей

Отклонение от круглости – наибольшее расстояние Δ от точек реального профиля до прилегающей окружности (рисунок 4.7, а). Допуск круглости Т – наибольшее допускаемое значение отклонений от круглости. Частными видами отклонений от круглости являются овальность и огранка (рисунок 4.7, б, в).

Отклонение от цилиндричности – наибольшее расстояние Δ от точек реальной поверхности вращения до прилегающего цилиндра в пределах нормируемого участка L (рисунок 1.8, а). Допуск цилиндричности Т – наибольшее допускаемое значение отклонений от цилиндричности (рисунок 4.8, б).

Рисунок 4.8 – Отклонения от цилиндричности и формы продольного сечения

Отклонение профиля продольного сечения – наибольшее расстояние Δ от точек образующих реальной поверхности в плоскости, проходящей через ее ось, до соответствующей стороны прилегающего профиля в пределах нормируемого участка - (рисунок 4.8, в). Частными видами отклонений от профиля продольного сечения являются конусообразность, бочкообразность и седлообразность (рисунок 4.8, г, д, е).

4.4.3 Нормирование отклонений и допусков формы плоских поверхностей

Отклонение от плоскостности определяют как наибольшее расстояние Δ от точек реальной поверхности до прилегающей плоскости в пределах нормируемого участка (рисунок 4.9, а). Допуск плоскостности – наибольшее допускаемое значение отклонений от плоскостности (рисунок 4.9, б). Частными видами отклонений от плоскостности являются выпуклость и вогнутость (рисунок 4.9, в, г).

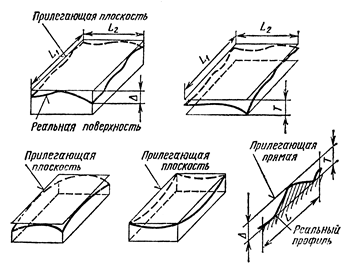
Рисунок 4.9 – Отклонения формы плоских поверхностей

Отклонение от прямолинейности в плоскости определяют как наибольшее расстояние Δ от точек реального профиля до прилегающей прямой (рисунок 4.9, д).