Система нормирования отклонений формы и расположения поверхностей

Под отклонением формы поверхности (или ее профиля в сечении) понимают отклонение формы реальной поверхности (реального профиля) от формы номинальной поверхности (номинального профиля), заданной чертежом. При этом, как правило, шероховатость поверхности, полученная в результате механической обработки, не учитывается. В основу нормирования и количественной оценки отклонений формы и расположения поверхностей положен принцип прилегающих прямых, поверхностей и профилей.

Прилегающая прямая – прямая соприкасающаяся с реальным профилем и расположенная вне материала детали так, чтобы отклонения от нее наиболее удаленной точки реального профиля в пределах нормируемого участка имело минимальное значение (рисунок 4.6, а). Соответствующее расположение имеет прилегающая плоскость относительно реальной поверхности.

Прилегающая окружность – это окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения (рисунок 1.6, б), или максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения (рисунок 4.6, в).

Соответствующее расположение имеет прилегающий цилиндр относительно реальной поверхности вращения.

При измерении прилегающие профили и поверхности реализуются рабочими кромками поверочных или лекальных линеек, поверхностями контрольных плит и оправок и т. д.

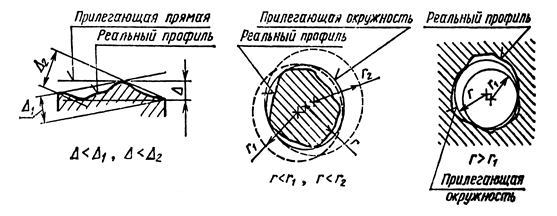
Рисунок 4.6 – Прилегающая прямая (а) и окружность (б)

Количественно отклонения формы оценивают наибольшим расстоянием Δ от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней.

Приняты следующие обозначения: Δ – отклонение формы или отклонение расположения поверхностей, Т – допуск формы или допуск расположения, L – длина нормируемого участка поверхности (профиля).