ЛИШНИЙ ВЕС. Процесс теплопроводности – один из, так называемых, процессов тепломассопереноса, играющих огромную роль в природе и в технике

Процесс теплопроводности – один из, так называемых, процессов тепломассопереноса, играющих огромную роль в природе и в технике. Другие процессы такого рода – диффузия, благодаря которой смешиваются разные жидкости или газы, процессы гидродинамики и аэродинамики (переноса жидкостей и газов).

Хотя каждый из таких процессов имеет собственные закономерности, между ними много общего:

1) эти процессы происходят в сплошной среде;

2) при их математическом моделировании используется один и тот же математический аппарат – дифференциальные уравнения в частных производных.

Понятие «сплошная среда» широко используется в науке. Во многих ситуациях жидкости, газы, твердые тела можно рассматривать как «сплошные», отвлекаясь от их молекулярного и атомарного устройства. Например, при изучении процессов распространения тепла или диффузии можно отвлечься от атомарного строения вещества и оперировать такими характеристиками как теплоемкость, теплопроводность, скорость диффузии и др., которые можно исследовать и практически использовать без выяснения их микроскопической природы.

В приближении сплошной среды свойства объекта описываются математически с помощью непрерывных функций координат и времени: f(x,y,z,t). За каждым свойством закрепляется своя функция, связь между ними дает полное описание среды.

Существующие задачи можно разделить на два класса: статические и динамические. В первом случае значения величин, характеризующих сплошную среду, не зависят от времени – f(x,y,z). Требуется найти их пространственное распределение – поле распределения. Во втором случае f(x,y,z,t) и нужно дать описание полей распределения во времени. Например, исследовать изменение температуры в разных точках тела, которое подогревается от источников тепла, интенсивность которых меняется со временем.

Ограничимся одной из самых простых задач данного класса – переносом тепла в однородном стержне. Рассмотрим линейный стержень, боковая поверхность которого не проводит тепла (теплоизолирована). Если в начальный момент стержень неравномерно нагрет, то в нем будет происходить перераспределение тепла. При отсутствии внутренних источников тепла его температура, в конце концов, выровняется.

Поскольку стержень линеен и однороден, то распределение температуры в пространстве характеризуется одной координатой х.

Температура (обозначим ее u) зависит от х; кроме того, она может меняться со временем, т.е. является функцией двух переменных u(x, t). Изменение этой функции вдоль стержня определяется производной по х, а изменение ее со временем определяется производной по t. Они взаимосвязаны и входят в одно уравнение.

Уравнение теплопроводности.Выведем уравнение, описывающее процесс изменения температуры в стержне. Зафиксируем некоторую точку х₀ и выделим около нее малый участок стержня длиной .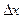

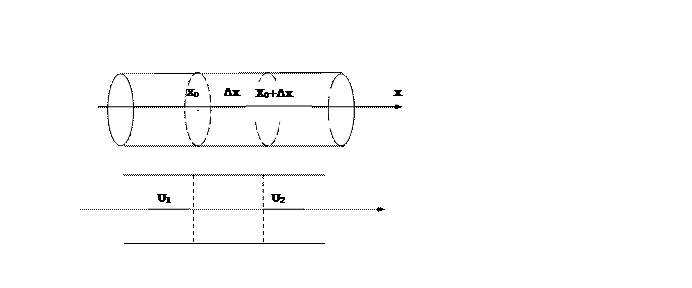Искомое уравнение есть уравнение теплового баланса, т.е. изменение количества тепла в избранном участке стержня за счет притока и (или) оттока его через два сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью. Выразим все это математическим языком.

Количество тепла, проходящее через поперечное сечение стержня в точке х₀за время 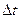, пропорционально площади сечения S, градиенту температуры 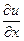и промежутку времени : ~ .

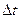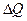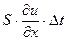Если с S и 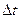все очевидно, то появление 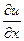требует пояснений. Из экспериментов известно, что поток тепла 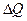через некоторый участок стержня длиной 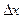тем больше, чем больше разность температур 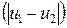на его концах и чем меньше расстояние :

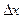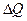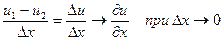
Вводя коэффициент пропорциональности k, называемый коэффициентом теплопроводности, получаем

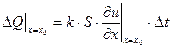(1)

Значение k определяется материалом стержня в единицах системы СИ:

материал	Теплопроводность (Вт/м·К)
Медь Сталь Кирпич Дерево Воздух	0,7 0,1 0,034

Таким образом, различия в теплопроводности разных материалов огромны.

Теперь запишем количество тепла, проходящее через сечение в точке 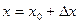. Оно определяется той же формулой:

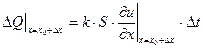
с условием, что производная 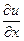берется в точке 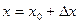. Для получения искомого уравнения ее надо выразить через значение в точке х₀.

Имеем разложение в ряд, ограничиваясь первым порядком приращения ,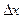

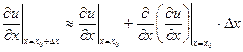
в силу чего получим:

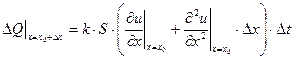(2)

Из (1) и (2) видно, что через сечения 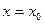и 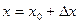за время 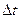прошло разное количество тепла, поэтому та его часть, которая пошла на нагревание (или, в зависимости от знака, на охлаждение) этого участка стержня, есть

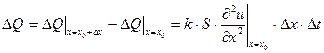
Пусть за то же время температура участка изменилась на 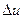; как известно, это связано с изменением тепла 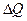, которое выражается соотношением:

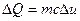где m – масса, c – удельная теплоемкость. Приравняем два выражения для :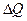

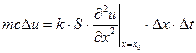
Поскольку массу можно представить как 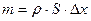(ρ – плотность вещества), то, поделив обе части уравнения на 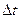и перейдя к пределу при 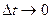, получим

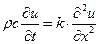В это выражение входят три постоянные, характеризующие вещество. Удобно объединить их в одну постоянную 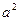, где 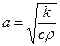-- так называемый, коэффициент температуропроводности. Обозначение 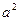удобно, так как фиксирует знак этого коэффициента – он всегда положителен.

Тогда перепишем уравнение в виде

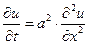(3)

Это – основное уравнение теплопроводности для однородного стержня. Как следует из процедуры вывода, это уравнение локально, т.е. в данный момент времени и в данной точке выражает закон сохранения энергии.

Уравнение (3) – одно из самых простых дифференциальных уравнений в частных производных. Несмотря на его элементарный вид, решение такого уравнения даже в простейшей ситуации есть весьма сложная задача.

Начальные и краевые условия. Уравнение (3) описывает процесс изменения температуры стержня во времени и в пространстве. Для решения задачи надо знать распределение температуры в теле в некоторый начальный момент времени:

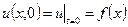,(4)

где 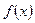--заданная функция.Кроме того, в тех местах, где возможен теплообмен с окружающей средой, надо знать условия этого теплообмена. Для стержня с теплоизолированной боковой поверхностью такими местами являются концы. Пусть длина стержня l. Если один конец имеет координату х = 0, а другой – х = l, то простейший вариант краевых условий – постоянная температура на каждом конце стержня:

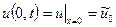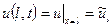, (5)

Нижеследующее утверждение физически очевидно, но его строгое математическое доказательство весьма непросто: дифференциальное уравнение (3) при начальном условии (4) и краевых условиях (5) имеет единственное решение.

Аналитические методы решения задачи одномерной теплопроводности существуют, но требуют значительной математической подготовки. Решение обычно получается в виде ряда Фурье, однако по его виду протекание процесса неочевидно, оно требует визуализации на компьютере. В двух- и трехмерном случаях аналитическое решение чаще всего получить не удается. Решим задачу численно, используя вычислительный эксперимент.

Используем методы конечных разностей. Покажем на примере уравнения теплопроводности наиболее распространенные методы численного интегрирования уравнений в частных производных. В их основе лежит прием дискретизации.

Покроем отрезок стержня [0, l] одномерной сеткой (т.е. разобьем на n равных частей) с узлами в точках

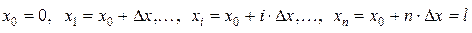
Искомую функцию u(x) будем аппроксимировать ее значениями в узлах сетки.

Остановимся на разностной аппроксимации производных. Производная 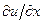связывает значения 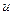в соседних узлах сетки. Очевидная аппроксимация первой производной в точке 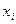имеет вид

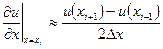(6)

Для крайних точек, однако, такая аппроксимация невозможна, и простейший способ – ограничиться односторонними разностями:

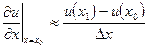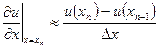, (7)

Выражения (6) и (7) дают простейшие аппроксимации. Рассматривая большее количество узлов, можно получить аппроксимации более высокого порядка. Аппроксимация вторых производных имеет вид

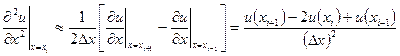, i = 1, 2, …, n – 1 (8)

В уравнении (3) есть производная по t: 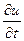. Для нее также нужна аппроксимация, поэтому возникает еще одна – временная сетка. При интегрировании уравнений по времени мы движемся по отдельным временным слоям, а в каждом слое определяем значения искомой функции на пространственной сетке. Если для интегрирования по времени используется метод Эйлера или другой одношаговый метод, то для работы со следующим временным слоем используются значения искомой функции из предыдущего слоя (для более сложных методов – из нескольких предыдущих слоев).

Далее будем индексы, соответствующие временной сетке, писать вверху (надстрочно), а пространственной – внизу (подстрочно). Таким образом, для одномерного уравнения запись 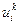означает значение функции 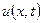в k-м временном слое и в i-м узле пространственной сетки.

Рассмотрим уравнение теплопроводности (3) и сформулируем простейшую возможную схему его интегрирования – явную схему первого порядка – по времени, используя метод Эйлера. По пространству – используем простейшие аппроксимации (8). Шаг по времени обозначим 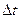, по координате – .

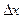Температуру на новом временном слое для внутренних узлов выразим через температуру на предыдущем временном слое, т.е. 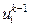через .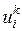

Запишем уравнение (3) для дискретной функции :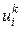

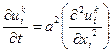
Обозначим правую часть уравнения (3) для дискретной функции :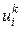

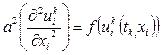
Запишем метод Эйлера для функции 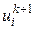на новом временном слое k+1 с использованием аппроксимации (8):

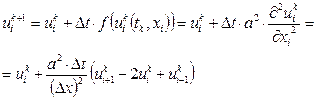
В итоге получим

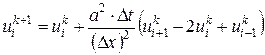(9)

Это явная разностная схема по времени. Она записана для внутренних узлов сетки. Здесь k = 0, 1, …; i = 1, 2, …, n – 1 (краевые точки i=0, i=n не включены).

В силу начального условия (4) в начальный момент времени (при k=0):

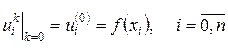
где функция 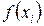задана и определяет значение температуры на нулевом слое.

Значения на концах стержня 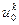и 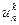зависят от типа краевого условия (5), когда концы стержня поддерживаются при постоянной температуре, имеем:

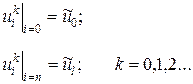
где 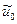, 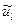-- заданные числа.

Теперь остановимся на вопросе об устойчивости и эффективности метода. Поскольку схема (9) явная, тo она относится к условно устойчивым разностным схемам. Существуют разностные схемы:

§ абсолютно неустойчивые,

§ абсолютно устойчивые

§ условно устойчивые.

Первые при любых, сколь угодно малых, шагах так «раскачивают» начальную погрешность, что приводят к результатам, не имеющим общего с реальностью.

Вторые ни при каких шагах не «раскачиваются», хотя, конечно, чем меньше шаг, тем меньше разница между приближенными и точными решениями.

Третьи устойчивы при одних комбинациях значени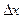й и 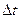и неустойчивы при других. Доказано, что разностная схема (9) устойчива при

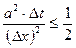(10)

и неустойчива в противном случае.

ЛИШНИЙ ВЕС

НОВАЯ ДИЕТОЛОГИЯ

ОГЛАВЛЕНИЕ

Предисловие. 4

Глава 1. Диетология – учение о рациональном питании. Главное положение диетологии содержит серьезную ошибку. 8

Глава 2. Можно ли похудеть быстро?. 19

Глава 3. Реклама совестливая, просто реклама, реклама бессовестная и реклама Демиса Русоса. 26

Глава 4. Врач Алэн Голэй и его «эффект йо-йо», или диетолог-фокусник из Женевы 29

Глава 5. Второе основное положение диетологии – сбалансированность питания 33

Глава 6. Шведский профессор Арне Аструп и его сенсационная «малая революция» в диетологии – расчет на простаков. 39

Глава 7. Центры голода и насыщения в гипоталамусе человека и животных. 42

Глава 8. Третье основное положение диетологии – строгое соблюдение режима питания, но только не по Шелтону! 56

Глава 9. Не надо считать калории, следите за показаниями весов. Универсальный режим питания в «премиальным регулятором». 70

Глава 10. Полные хотят худеть быстрее и без насилия над собой. 75

Глава 11. Бизнес на лишнем весе. Делайте свой гербалайф сами! 83

Глава 12. Лекарственные средства против полноты и ожирения. 92

Глава 13. Почему другие едят больше и не полнеют? Исправление ошибки в главном положении диетологии. 102

Глава 14. «Ожирение – неизбежность» и «ожирение – рабочий вариант жизни» 129

Глава 16. Главная ошибка Герберта Шелтона – раздельное питание. Особенно для России и Японии. 138

Глава 17. Прогрессирующее ожирение со снижением половых функций организма 149

Глава 18. Ударим физическими нагрузками по стрессам и ожирению?. 154

Глава 19. Полноте и ожирению «великие мира всего более подвержены, нежели подлый люд», особенно с «кремлевскими таблетками». 160

Глава 20. Третья жертва мадам Шалон. 163

Заключение. 166

Предисловие

Эту книгу можно считать своеобразным диетологическим детективом, в котором впервые излагается целый ряд новых научно обоснованных положений их этого раздела современной медицины.

«Диетологический детектив» берет свое начало с публикаций нашего соотечественника академика А.М. Уголева, который сформулировал знаменитые три важнейших положения теории питания. Главное их этих положений: калорийность пищевого рациона должна соответствовать энергозатратам организма. Вот уже тридцать лет все диетологи мира повторяют это главное правило диетологии как молитву. Но именно это важный тезис науки о рациональном питании содержит серьезную ошибку: не калорийность пищевого рациона, а калорийность усваиваемой каждым организмом по-разному основной части пищевого рациона должна соответствовать энергозатратам организма.

Этот вопрос впервые исследуется в настоящей книге.

Лучшие диетологи Европы (профессор Арне Аструп из Швеции и другие) постарались внести свой «революционный вклад в современную науку о питании.

Однако самый разрушительный, на наш взгляд, вклад в диетологию внесли знаменитые американские авторы Поль Брэгг, Герберт Шелтон, Норманн Уокер и другие. В нашей книге «Новое понимание сахарного диабета» (С.-Петербург, 1997) уже подробно рассматривались некоторые диетологические ошибки Поля Брэгга, главной из которых является голодание. В этой книге мы попытаемся исследовать диетологические «новшества» известных зарубежных диетологов и проанализировать их просчеты. В частности, мы остановимся на анализе заблуждений сторонников раздельного питания по Шелтону и ошибок самого Герберта Шелтона в вопросах, относящихся к режиму питания.

Нашедшие признание в современной медицине представления о проявлениях гипоталамических центров голода и насыщения в организме человека совершенно очевидно противоречат некоторым фактам (особенно гипергликемическим состояниям при сахарном диабете) и широко известным экспериментальным данным. Это привело к чрезвычайно распространившейся ошибке о регулировании приема пищи не только чувством голода, но и чувством насыщения.

В этой книге автор существенно переработал принятые в медицине положения о проявлениях деятельности центра насыщения. Впервые доказано, что вместо чувства насыщения, генерируемого соответствующим центром гипоталамуса, природа дала человеку ощущение наполнения желудка еще не переваренной пищей. И этим чувством необходимо научиться разумно пользоваться как показателем насыщения.

В последние годы по России прокатилась огромная волна мошеннического бизнеса, основанного на страстном желании полных людей избавиться от лишнего веса, бизнеса, хорошо организованного и безжалостного к своим жертвам. Следовало ожидать, что лучшие ученые-диетологи России дадут точную научную оценку каждому их вариантов такого бизнеса. Но случилось непредвиденное: ученые диетологи сами занялись рекламированием сомнительных средств, якобы способных избавить всех желающих от лишних килограммов. Диетологический детектив оказался серьезно продолженным. Одной из целей, преследуемых автором, является исследование и научная оценка основных вариантов бизнеса на лишнем весе людей.

Ошибки диетологов проникли в большое количество книг, газетных и журнальных статей. Введенные в заблуждение подобными материалами, лживой, но умело построенной «фирменной» рекламой читатели не имеют правильного представления о действительно научных положениях диетологии. Настоящая книга призвана помочь читателям сориентироваться в этом море околонаучной литературы и предлагает только научно обоснованные диетологические знания.

Кто же эти уже полные или пока еще стройные люди, которым предстоит стать жертвами ошибок знаменитых отечественных и зарубежных диетологов и источником доходов дельцов бизнеса от медицины?

Полных людей можно разделить на три группы.

Первая групп – полные люди, которые не желают худеть. Это их личное дело и никто не вправе их за это осуждать. Возможно, они захотят прочитать эту книгу и Вилу естественной любознательности и смогут, наконец, узнать, чем им грозит полнота.

Вторая группа – полные люди, которые хотят похудеть, чтобы выглядеть привлекательнее. Но эти люди обычно очень плохо осведомлены о проблеме похудения и часто оказываются под влиянием интригующей и одновременно обманывающей рекламы ненасытных фирм. Полным людям, мечтающим сбросить лишние килограммы, очень полезно предварительно прочитать эту книгу, чтобы приобрести недостающие знания и самим безошибочно ориентироваться в вопросах диетологии и худения.

Но есть третья группа полных людей, которым необходимо похудеть в обязательном порядке для спасения своего здоровья, а иногда – и жизни. Эту группу составляют полные люди, больные сахарным диабетом II типа (инсулиннезависимый тип) или III типа (сочетанный вариант сахарного диабета II и I типов).

Во время работы над книгой «Новое понимание сахарного диабета» автор установил: полные люди, болеющие сахарным диабетом, в такой степени дезориентированы современной медициной в вопросах своего заболевания, что не имеют представления о возможностях его лечения и излечения. Эти люди заболели сахарным диабетом II типа из-за переедания или чрезмерного усвоения углеводов организмом. Такие больные составляют 72% от общего числа больных сахарным диабетом, и их излечение находится, в первую очередь, в их собственных руках. Эти полные люди должны помочь себе сами, они просто обязаны значительно похудеть, восстановив этим свое здоровье, а после его восстановления нормально питаться. Вот и все.

Здоровье полных людей именно этой, третьей, группы особенно беспокоит автора. Прежде всего, им необходимо прочитать нашу книгу «Новое понимание сахарного диабета», а уже затем – данную книгу, чтобы получить необходимые знания и не стать очередной жертвой рекламы какой-нибудь модной фирмы. Автор заверяет читателей, что другой литературы, содержащей равноценные знания, просто не существует. Эти знания являются «ноу-хау» автора, которым он принял решение поделиться с читателями.

По отношению к полным людям, больным сахарным диабетом II или III типа, современная фирменная реклама разнообразных средств похудения, в большинстве своем, приобретает смысл недопустимо безнравственных публикаций. Особенно недопустимо участие в такой рекламе представителей медицины. По смыслу профессии!

Читателям следует обратить внимание на теоретические обоснования применения акупунктуры (иглоукалывания) для похудения. впервые изложенные в этой книге.

Автор ожидает, что разработанный им универсальный режим питания с «премиальным регулятором» также заинтересует читателя.

Особое внимание в этой книге уделяется воспитанию у читателя самостоятельности в принятии решений, касающихся вопросов диетологии и худения.

Надеемся, чтение этой книги будет познавательным и вместе с тем интересным.

<12 3 4 5 6 7 >

Дата добавления: 2015-01-13; просмотров: 920;