Частные случаи стесненного падения

Выделяют 4 вида стесненного падения: 1)Одиночного тела в однородной среде, огранич-й стенками; 2) масса однородных тел. Однородные тела облад. одинаков. 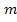, ,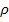крупностью. Изучение массы падающих тел отлич-ся крупностью наиболее сложно для изучения.

1)Падение одиночного тела в однородной среде с ограничительной стенкой. Движ-е ч-ц в узких трубках с некоторым приближением м/рассм-ть как случай стесненного крупного дв-я ч-ц. Таким путем ученым Монро была получю 1 ф-ла для опред-я 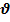стеснен.падения. Послед-ми работами было уст-но, что закономерности падения ч-ц в узких трубках, применяемых лишь д/качеств. Описания стесн-го пад-я и не дают достаточно точно колич-х завис-тей. Эксперим-ое измер-е 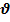произв-сяпутем опред-я 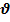восходящего потока взвеш-х ч-ц. 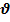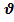_{ст.= а} (ск-ть восходящего потока).Ск-ть м/опред-ть с пом-ю высоты: 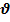_ст.=H/t. Нач. и конец отсчета t м/фиксир-ть как визуально, также с прим-ем эл-магн., радиактив-го и др. методов. Для расчета 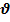_пад. единичного шара в трубке, предложен ряд ф-л, в кот-х 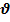_ст.пад. вычисл-ся как 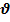_{своб.пад.,}умнож-го на коэф-т, завис-ий от соотнош-я d ч-цы к d трубки, в кот-й происходит падение: 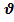_{ст.пад.= 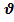0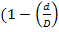} ^1.5), где 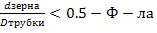Монро пригодна при отн-ии _.

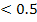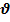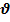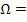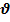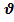2)Падение масс однородных зерен. Эксп-но _пад. масс однор-х зерен опред-ся как потока, в кот-й взвешен опред-й объем ч-ц. При небольшой конц-ции Const при этом _{ст.= а}(ск-ть восходящего потока), кот. опред-я как отношение объема взвешивающей среды Q к площади проходящей в ед-цу времени к площади сеч-я в данной трубке: 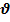_а=Q/S(см³/с). Для опред-ия скор-й стесн-го пад-я однор-х ч-ц предложены 2 осн. группы формул:

1. Ф-лы, основанные на рассм-ии массы пад-х зерен как фильтрац-ой среды, ч/з кот. жид-ть протекает в вертикальном направл. снизу вверх.

2. Ф-лы, основ-ые на рассм-и падения в жид-ти отдельной ч-цы, наход-ся в массе других. Хотя 1-ая концепция(1сл) имеет более выраж-й физ-й смысл, недостатком формул этой группы яв-ся ограничения их применения небольшими коэф. разрыхления: m<0,8 д/кот-х взвешенный слой м/рассм-ся как пористая среда: ,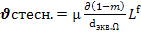

L=Ar 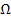³m³{216(1-m)}, где Ar- число Архимеда, Ar= Re² 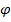(1 пар-р Лящ.), коэф. 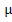и f, пар-ры, зав-ие от L.

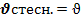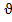Из ф-л 2 гр. наиб. распр. яв-ся ф-ла Лященко: ₀ mⁿ= ₀(1- 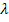)ⁿ, n-показатель степени, зав-й от размера, плотности, формы ч-ц: n=4.65-экспер., если Re<0.5(ламин. режим пад. зерен в стеснен-х усл-х). Re>500 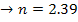; 0.5<Re<500 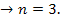Исп-ся граф. методы для опред.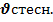

3)Падение отдел-х крупных зерен в массе окруж-х мелких. Этот сл-й исп-ся при обог-ии мат-ла в тяж. суспензиях. Важно, что в 1-ой и той же суспензии тела одинак. плотности, но разного размера м/перемещаться по разному: крупные тела б/тонуть, а мелкие всплывать или нах-ся в равновесии. Это огранич. нижний предел крупности ч-ц обогащаемых суспензий(по ф-ле Ньют-Риттенгера). Экспер-ое опред. падения ч-ц суспензии м/проводится н-р, в вертикальных трубках. В этом случае исп. как неподвиж. и движ. суспензии. 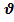м/опред. как путем фиксации времени прохождения 2-х отметок (нач. и кон. пад.) м/исп. эл.маг. катушки (тело снабж. магнитным сердечником).

4) Массовое падение разнородных зерен.- падение разнор-х, но соизмеримых по размерам ч-ц, в отличии от сл.3),в кот. падающие ч-цы отлич-ся на неск-ко поряков.Такой вид падения встреч-ся в классиф-х,отсад-х машинах, на конц-х столах и ряде др-х грав-х апп-в. Совмест-ое падение разнород-х ч-ц изучено в незнач-й степени. В ряде работ д/экспер-го опред-я 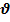ч-ц в поле дисперсной пульпы различ. размеров, применен. косвен. м-д, основ-й на исп-ии разницы в содерж-и ч-ц узких классов в пульпе, нах-ся внутри апп-та и вых-щей из него. Качественная картина при движ-и ч-ц, соизмер-х по размерам след-ая: при Соnst объем. содержании твердого 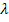скор. круп-х ч-ц в присутствии мелких умен-ся по срав-ю со 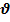их стесн-го пад-я, при наличии ч-ц 1-го крупного класса и наоб-т 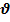мелких ч-ц в присут-и крупных увел-ся.