Как сделать самодельный черный глобус

Черный глобус — чрезвычайно ценное наглядное пособие при изучении основ астрономии в школе. Его можно изготовить из географического глобуса достаточно больших размеров. Если же такого глобуса в школе нет, то его можно сделать из папье-маше на занятиях астрономического кружка.

Из прямоугольного листа фанеры вырезать полукруг, а оставшуюся часть прикрепить к столу при помощи петель (рис. 162). Это так называемый перекидной шаблон.

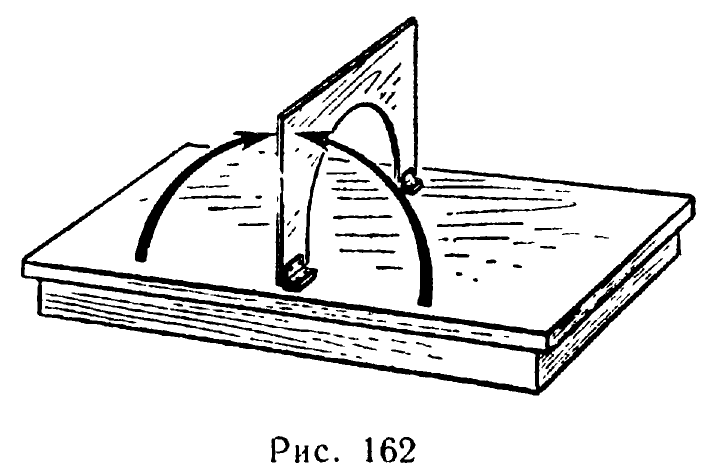
Далее, проворачивая фанеру то в одну, то в другую сторону до отказа, подкладывать в отверстие влажную глину до тех пор, пока глина не примет форму правильного полушария.

Глину нужно покрыть сплошным слоем мелко нарезанных кусочков газетной или оберточной бумаги. Первый слой бумаги будет держаться на влажной глине без клея, следующие четыре-пять слоев приклеить мучным клейстером. Для того чтобы покрытие было равномерным, нужно пользоваться двумя сортами бумаги — оберточной и газетной, или оберточной бумагой двух сортов и чередовать слои: например, если первый слой из газетной бумаги, то второй должен быть из оберточной, третий опять из газетной и т. д.

Снимать полушарие с формы можно только тогда, когда клейстер окончательно просохнет.

Изготовленные таким образом два полушария сшить тонкой проволокой и шов заклеить бумагой. Глобус нужно окрасить тушью или покрыть чёрным лаком. Никаких линий и точек или изображений созвездий на глобус наносить не следует.

Готовый глобус поместить внутрь подвижной армиллярной сферы (рис. 163). Кольцо NWS изображает математический горизонт, P’SPN — небесный меридиан. Кольцо меридиана может свободно поворачиваться в пазах кольца NWS и упора К. Черный глобус подобен классной доске в том смысле, что и на нем всегда можно начертить именно те линии, которые нужны для решения данной задачи.

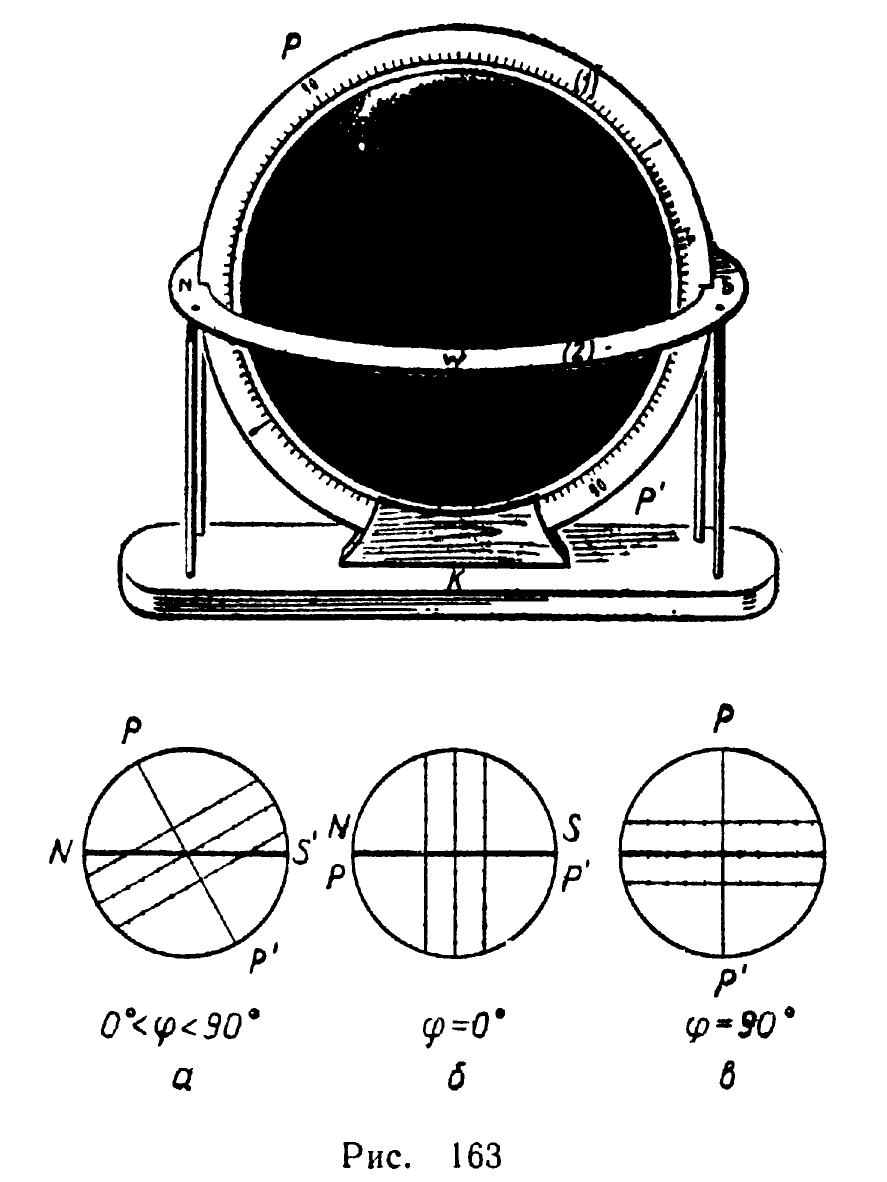
В качестве примера приведем одну из многочисленных задач, решаемых при помощи черного глобуса: описать характер суточного пути Солнца на разных широтах.

В дни равноденствий Солнце пересекает небесный экватор. Суточный путь Солнца в эти дни с большой степенью точности можно представить на глобусе как большой круг в плоскости небесного экватора. В день летнего солнцестояния склонение Солнца δ = 23 1/2°, и, следовательно, суточный путь его будет соответствовать малому кругу со склонением +23 1/2°. В день зимнего солнцестояния суточный путь Солнца соответствует малому кругу со склонением δ = 23 1/2°.

Начертим на глобусе большой круг в плоскости экватора. Для этого поворачиваем кольцо небесного меридиана так, чтобы нуль на шкале меридиана был против точки N на кольце горизонта, тогда плоскость небесного экватора совпадет с плоскостью математического горизонта. Теперь достаточно прикоснуться мелком к глобусу в какой-либо точке против кольца горизонта и, продолжая держать мел неподвижно, провернуть глобус вокруг оси на 360°.

Проводим параллель δ = 23 1/2°. Для этого, не перемещая оси глобуса относительно горизонта, прикасаемся мелом к глобусу в точке, находящейся против деления +23 1/2° на кольце меридиана, и проворачиваем глобус вокруг оси на 360°, держа мел неподвижно. Аналогично проводим параллель δ = —23 1/2°.

Полученные три круга изображают суточные пути Солнца в дни равноденствий и солнцестояний. Не нужно забывать, что эти пути Солнца — результат видимого вращения небесной сферы, а не пути его на небесной сфере.

Разделим каждый из этих кругов на двадцать четыре части. На большой круг деления наносим в соответствии со шкалой кольца горизонта через каждые 15°. Для того чтобы разделить малые круги, поворачиваем глобус вокруг оси и, когда деление большого круга придется против кольца небесного меридиана, наносим деления на малые круги в точках, также приходящихся против кольца меридиана. Так наносятся все деления.

Теперь можно решить задачу. Изучить суточные пути Солнца для средних широт в дни равноденствий и солнцестояний (0° < ф < 90°).

Устанавливаем глобус «по широте», т. е. поворачиваем его так, чтобы дуга NP равнялась ф (рис. 163, а). Суточные пути Солнца наклонны к горизонту. В дни равноденствий Солнце находится над горизонтом 12 ч (двенадцать делений большого круга над кольцом горизонта), в день летнего солнцестояния больше 12 ч, в день зимнего солнцестояния меньше 12 ч (сосчитать деления малых кругов над кольцом горизонта).

В дни равноденствий Солнце восходит в точке востока, заходит в точке запада, в день зимнего солнцестояния — восходит в юго-восточной части горизонта, заходит в юго-западной, в день летнего солнцестояния Солнце восходит в северо-восточной части горизонта, заходит в северо-западной.

Для данной широты можно определить азимуты точек восхода и захода по шкале кольца горизонта и высоту в кульминации по шкале кольца меридиана.

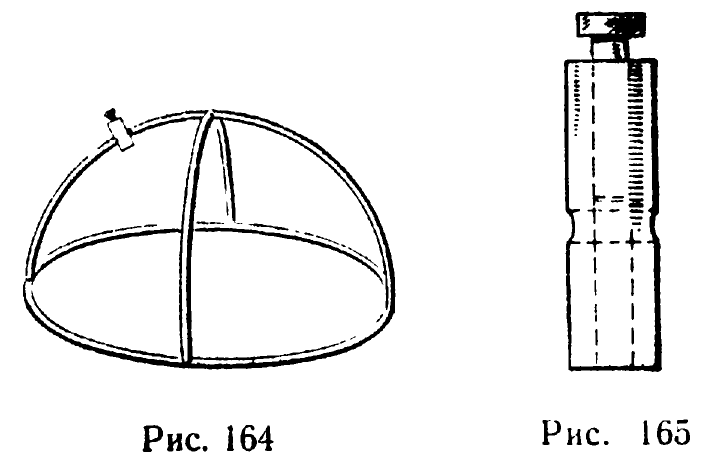
Горизонтальная сетка к черному глобусу. Предлагаемое пособие представляет собой сетку основных линий горизонтальной системы координат (горизонта, меридиана, первого вертикала), изготовленную из толстой проволоки (рис. 164). Вся сетка крепится на оси глобуса следующим образом. Вместо крепящей гайки-шарика на верхний конец оси навинчивается специальная втулка, изготовленная из меди или алюминия (рис. 165). В боковое отверстие втулки продевается дуга меридиана.

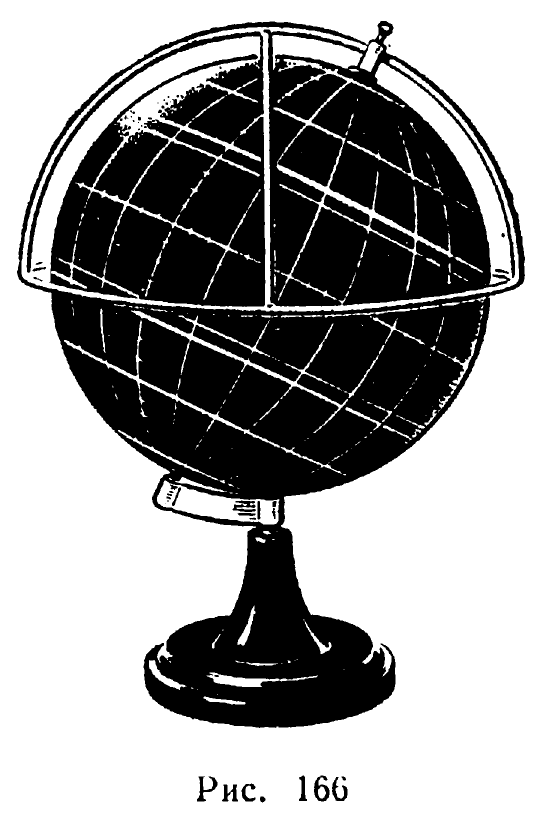
Сетка закрепляется во втулке верхним крепежным винтом (рис. 166). С помощью такой сетки и черного глобуса можно демонстрировать восход, кульминацию и заход светил, заходящие, незаходящие и невосходящие светила, изменение горизонтальных координат светил при суточном вращении небесной сферы, не говоря уже о наглядной демонстрации горизонта, меридиана и первого вертикала.