Системы координат в геодезии

Положение точек на физической Земной поверхности определяется принятой системой координат.

Координаты - это угловые и линейные величины, определяющие положение точек на поверхности Земли и в пространстве.

В геодезии применяются различные координатные системы. Рассмотрим некоторые из них.

Географические координаты - это широта (F) долгота (L) и высота (Н). Координатными плоскостями, относительно которых определяется положение точек, являются (рис. 1.2):

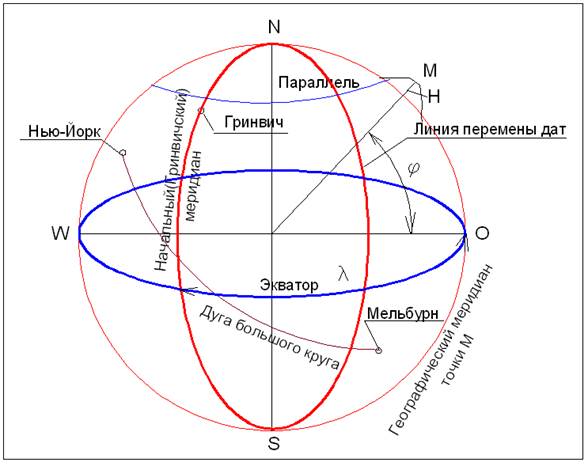
Рис. 1.2. Система географических координат.

Плоскость экватора, проходящая через центр эллипсоида перпендикулярно оси его вращения.

Плоскость начального меридиана – плоскость, проходящая через нормаль к поверхности эллипсоида в центре Гринвичской обсерватории (вблизи Лондона) и параллельная его малой оси.

Плоскость меридиана, проходящая через заданную точку Земной поверхности, называется плоскостью меридиана данной точки.

Географическая широта F - это угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью экватора.

Широты, отсчитываемые от экватора к северу называются северными и имеют знак «+», отсчитываемые к югу называются южными и имеют знак «-». По величине широта изменяется от 0⁰ до 90⁰.

Географическая долгота L - двугранный угол между плоскостями географического меридиана данной точки М и начального меридиана.

Отсчитывается от начального меридиана с Запада на Восток от 0⁰ до 360⁰ либо в обе стороны от 0⁰ до 180⁰, с указанием соответственно "восточная" и "западная".

Географическая высота H - расстояние по нормали от точки до ее проекции на поверхность эллипсоида.

Достоинство географических координат заключается в возможности обрабатывать результаты измерений в единой для всей поверхности Земли системе.

Большой круг (рис. 1.2) - линия пересечения земной поверхности с плоскостью проходящей через центр Земли. Дуга большого круга - кратчайшее расстояние между точками на земной поверхности.

Высота любой точки - есть расстояние от нее до уровенной поверхности. Превышением называется разность высот двух точек местности.

Применение географических координат для практических целей сопряжено с рядом трудностей:

- взаимное расположение точек определяется в угловых единицах, а все расстояния измеряются линейными мерами;

- значения одних и тех же угловых величин соответствуют разным линейным величинам в зависимости от широты места;

- использование географических координат связано со сложными расчетами.

В связи с этим географические координаты напрямую применяют только в мелкомасштабном картографировании.

Более простой системой являются плоские прямоугольные координаты. Решение геодезических задач в этой системе выполняется по простым формулам аналитической геометрии.

Однако для использования прямоугольных координат необходимо предварительно поверхность эллипсоида каким-то образом перенести (спроецировать) на плоскость. Такой перенос сопровождается неизбежными искажениями, величина и характер которых зависят от вида проекции.

Могут быть равноугольные, равновеликие и произвольные проекции.

Наиболее удобными для практических целей являются равноугольные проекции (сохранение углов и, следовательно, подобия объектов). В частности, наиболее широко с 1928 г. используется равноугольная поперечно - цилиндрическая проекция Гаусса - Крюгера.

Гаусс предложил эту проекцию, а Крюгер - разработал формулы для ее реализации.

Суть проекции:

- Земной эллипсоид разбивается меридианами на 6-ти градусные зоны (дольки) (рис. 1.3);

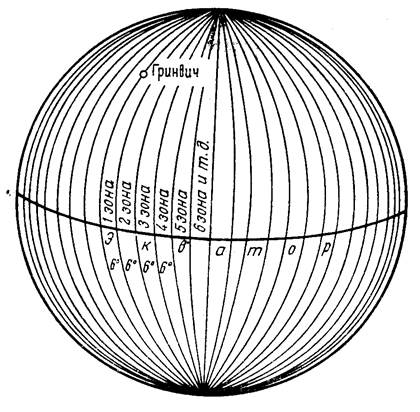
Рис. 1.3. Разбивка Земного эллипсоида на зоны.

- каждая зона проецируется на внутреннюю боковую поверхность цилиндра и касается его по среднему (осевому) меридиану;

- цилиндр разворачивается в плоскость.

В результате получается изображение, показанное на рис. 1.4.

Средний меридиан каждой зоны называется осевым, а крайние - граничными.

Осевой меридиан на плоскости изображается прямой линией без искажений и принимается за ось абсцисс, за ось ординат принимается экватор.

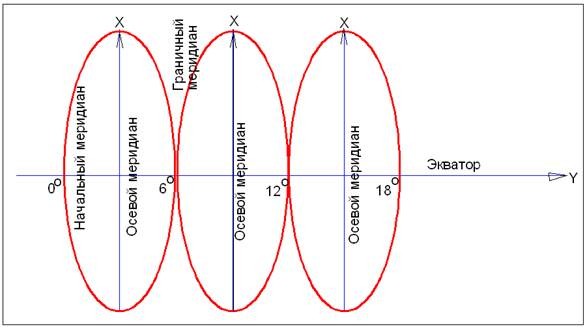
Рис. 1.4. Проекция Гаусса-Крюгера.

Таким образом, каждая зона имеет свою систему координат, в которой положение любой точки определяется ее расстоянием от осевого меридиана и от экватора. Зоны нумеруются арабскими цифрами от 1 до 60.

Так как территория России находится к северу от экватора, то все абсциссы точек здесь положительны. Чтобы избежать отрицательных ординат, начало координат принимают по оси ОY не 0, а +500 км. Такие ординаты называются преобразованными. При записи впереди ординаты указывают номер зоны. Так если точка А расположена в 12 зоне к западу от осевого меридиана на расстоянии 57235 м, а точка В - к востоку на 57235 м, то преобразованные координаты этих точек будут:

Ya = 500000 – 57235 = 442765 м;

Yb = 500000 + 57235 = 557235 м,

а с учетом расположения в 12 зоне Ya = 12 442765 м;

Yb = 12 557235 м.

Переход от расстояний на эллипсоиде к расстояниям на плоскости в проекции Гаусса-Крюгера связан с понятием масштаба изображения.

Масштаб изображения проекции m есть отношение бесконечно малого отрезка на плоскости dB к бесконечно малому отрезку на эллипсоиде dS, т.е. m = dB/dS.

В проекции Гаусса-Крюгера m зависит от ординаты точки Y:

m=1+Y²/2R² (R - радиус Земли).

Все расстояния измеряются на эллипсоиде. Для получения расстояний на плоскости надо применить формулу:

B = m S = S + Y²_m/2R²,

где Y_m=(Y₁+Y₂)/2 - преобразованная ордината средней точки линии.

Величина dS= Y²_m/2R² называется редукцией расстояния, она всегда положительна, то есть линия на плоскости больше линии на сфере. Из этой формулы видно, что искажения расстояний нарастают по мере удаления от осевого меридиана. На краю зоны dS порядка 1/1600 длины линии в средних широтах и 1/8000 - у полюсов.

Проекция Меркатора применяется в морских картах, при этом меридианы и параллели образуют прямоугольную сетку (рис. 1.5).

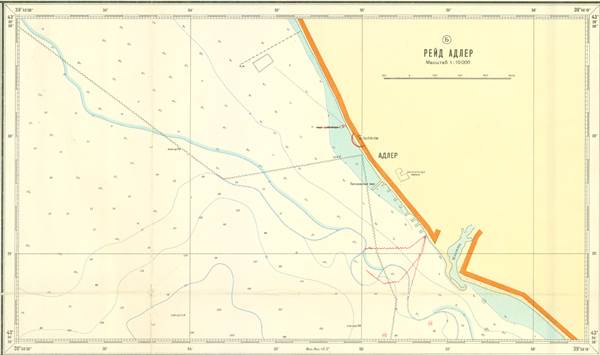
Рис. 1.5. Морская гидрографическая карта рейда Адлер.