Арифметическое среднее
Арифметическое среднее (арифметическая середина) определяется формулой:
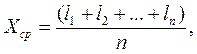 (1.8.5)
(1.8.5)
l1, l2,….ln - результаты равноточных измерений. Если неизвестно истинное (точное) значение измеряемой величины, что обычно и бывает на практике, то возникает вопрос, какую же величину принимать вероятнейшее значение. Для ответа на этот вопрос запишем результаты ряда равноточных измерений в виде:
Δ1 = l1 – X
Δ1 = l1 – X
……………..
Δn = ln – X
Cложив левые и правые части этих равенств получим
∑Δ = ∑l - nX. Разделив обе части этого равенства на n, будем иметь: 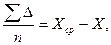 где Хср - Х = η - истинная погрешность арифметического среднего.
где Хср - Х = η - истинная погрешность арифметического среднего.
По третьему свойству случайных ошибок 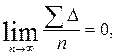 поэтому при n →∞ Хср→Х. Следовательно, при неограниченно большом числе измерений и отсутствии систематической ошибки, арифметическое среднее стремится к истинному значению измеряемой величины. Поэтому его называют вероятнейшим значением измеряемой величины. В практике число измерений естественно ограничено, поэтому арифметическое среднее может заметно отличаться от истинного значения.
поэтому при n →∞ Хср→Х. Следовательно, при неограниченно большом числе измерений и отсутствии систематической ошибки, арифметическое среднее стремится к истинному значению измеряемой величины. Поэтому его называют вероятнейшим значением измеряемой величины. В практике число измерений естественно ограничено, поэтому арифметическое среднее может заметно отличаться от истинного значения.
Дата добавления: 2014-12-17; просмотров: 1369;
