Формула полной вероятности. Формула Байеса. Пусть событие может произойти только вместе с одним из попарно несовместных событий (гипотез) , ,
Пусть событие 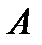 может произойти только вместе с одним из попарно несовместных событий (гипотез)
может произойти только вместе с одним из попарно несовместных событий (гипотез) 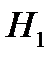 ,
, 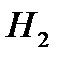 ,…,
,…, 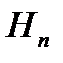 , образующих полную группу, т. е.
, образующих полную группу, т. е. 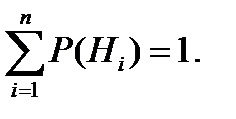
Вероятность события 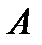 находится по формуле полной вероятности:
находится по формуле полной вероятности:
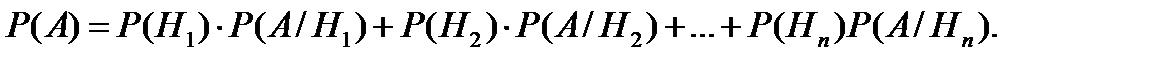 (3.16)
(3.16)
Если событие 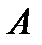 уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
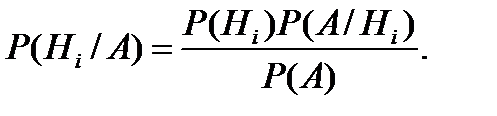 (3.17)
(3.17)
Пример 3.33. Имеются две одинаковых урны с шарами. В первой урне 5 белых и 10 черных шаров, во второй − 3 белых и 7 черных шаров. Выбирают наугад одну урну и вытаскивают из нее один шар.
1. Найти вероятность того, что этот шар белый.
2. Из наугад выбранной урны вытащили белый шар. Найти вероятность того, что шар вытащили из первой урны.
Событие 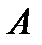 − вытащить наугад белый шар из выбранной наугад урны. Рассмотрим две гипотезы:
− вытащить наугад белый шар из выбранной наугад урны. Рассмотрим две гипотезы: 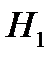 − выбрать наугад первую урну,
− выбрать наугад первую урну, 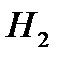 − вторую, причем
− вторую, причем 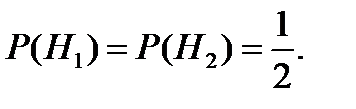 Вероятность вытащить белый шар из первой урны (условная вероятность)
Вероятность вытащить белый шар из первой урны (условная вероятность) 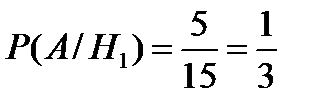 , а вероятность события
, а вероятность события 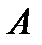 при условии, что событие
при условии, что событие 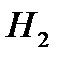 произошло
произошло 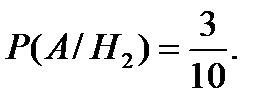 Используя формулу полной вероятности (3.16), получим:
Используя формулу полной вероятности (3.16), получим:
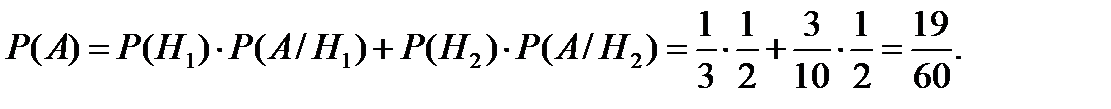
Известно, что из выбранной наугад урны вытащили белый шар, т. е. событие 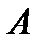 произошло. Необходимо найти вероятность гипотезы
произошло. Необходимо найти вероятность гипотезы 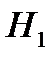 (была выбрана наугад первая урна) при условии, что событие
(была выбрана наугад первая урна) при условии, что событие 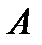 произошло, т. е.
произошло, т. е. 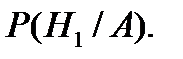 Используя формулу Байеса (3.17), получим:
Используя формулу Байеса (3.17), получим:
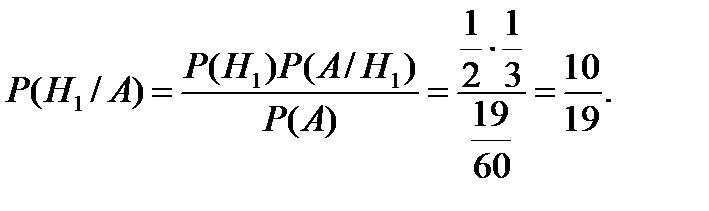
Дата добавления: 2014-12-14; просмотров: 993;
