Пример 2.1. Исследовать функцию на непрерывность:
Исследовать функцию на непрерывность:

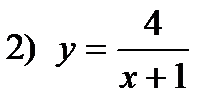 .
.
Решение.
1. Каждая из составляющих функций является элементарной, значит, каждая из них непрерывна во всех точках, в которых она определена. Точки, «подозрительные» на разрыв: х = 0, х = 1.
Пусть x = 0.
y(0) существует, у(0) = 3∙0 = 0.


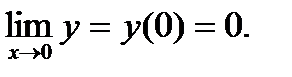
Следовательно, в точке х = 0 функция непрерывна по определению.
Пусть х = 1.
y (1) существует; у(1) = 2.
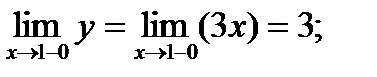

3 ≠ 2, следовательно, точка х = 1 является точкой разрыва 1-го рода (скачок).
2. D(y): x ≠ 1.
Т. к. в точке х = 1 функция не определена, то это точка разрыва.
 точка разрыва второго рода.
точка разрыва второго рода.
2.10. Найти точки разрыва функций:
1)  ; 2)
; 2)  ;
;
3)  4)
4) 
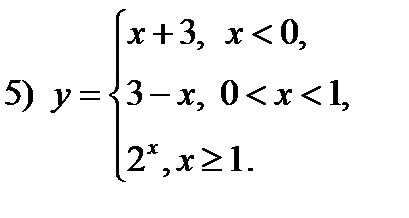
2.11. Исследовать функции на непрерывность:
1)  ; 2)
; 2) 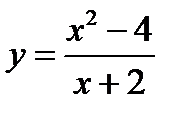 ; 3)
; 3) 
4) 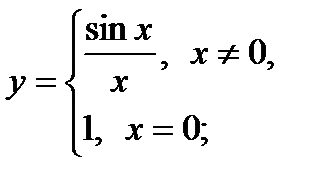 5)
5)  ; 6)
; 6)  ;
;
7)  8)
8) 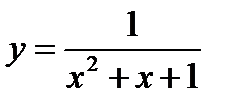 ;
; 

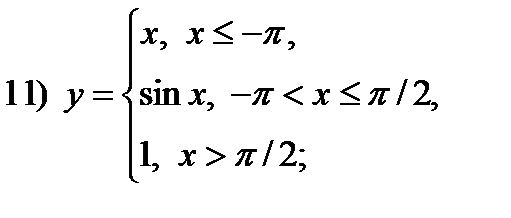

Дата добавления: 2014-12-14; просмотров: 3049;
