Конспект лекций по дисциплине
Теорема.Необходимым и достаточным условием совместности системы m линейных уравнений с n неизвестными
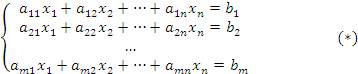
| (1) |
является равенство между собой рангов коэффициентной A и расширенной 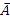 матриц.
матриц.
В русско-язычной литературе на эту теорему ссылаются как на теорему Кронекера-Капелли.
Следствия.
- Если rankÃ=rankA и совпадает с числом n неизвестных, то система (1) имеет единственное решение.
Это утверждение по сути представляет собой просто другую формулировку правила Крамера
- Если rankÃ=rankA>n, то система (1) имеет бесконечное множество решений.
Схема:
Равенство рангов коэффициентной и расширенной матриц означает совместность системы уравнений (1). При этом число r=rankÃ=rankA устанавливает количество базисных переменных, тогда как остальные (n - r) переменные играют роль свободных параметров и могут принимать любые значения. Каждому набору параметров, число которых бесконечно велико, соответствует свое решение.
Примеры:
1. Докажем необходимость условия, сформулированного в теореме, т.е. покажем, что предположение о совместности системы уравнений влечет за собой равенство рангов, 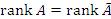 .
.
Рассмотрим расширенную матрицу

и преобразуем ее, выполнив элементарные операции над столбцами.
Вычтем из последнего столбца первый столбец, умноженный на 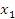 , второй столбец умноженный на
, второй столбец умноженный на 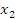 , и т.д. При этом ранг матрицы не меняется:
, и т.д. При этом ранг матрицы не меняется:
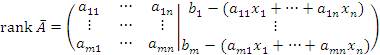
С учетом уравнений (1), последний столбец является нулевым и поэтому его можно опустить. Тогда
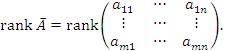
2. Перейдем к доказательству достаточности условия.
Покажем, что равенство рангов r=rankÃ=rankA влечет за собой совместность системы (1).
Если r= rankA , то существует несингулярная подматрица Ã r-го порядка. Ее матричные элементы (коэффициенты при неизвестных) указывают – какие именно r уравнений "образуют базис" данной системы уравнений - в том смысле, что каждое из оставшихся уравнений является следствием "базисных" уравнений (их линейной комбинацией).
Поэтому можно перейти к укороченной системе r уравнений и выбрать r неизвестных в качестве базисных переменных. Остальные (n - r) переменные будут при этом выступать в качестве свободных параметров, которым можно придавать произвольные числовые значения.
Укороченная система r линейных уравнений полностью эквивалентна исходной системе и имеет (согласно теореме Крамера) единственное решение для любого набора значений свободных параметров.
Примеры:
1. Дана система линейных уравнений,
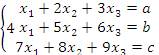 Установить соотношения между параметрами a, b и c, при которых система является несовместной. Решение. Составим расширенную матрицу и преобразуем ее к ступенчатой форме:
Установить соотношения между параметрами a, b и c, при которых система является несовместной. Решение. Составим расширенную матрицу и преобразуем ее к ступенчатой форме:
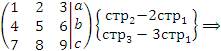 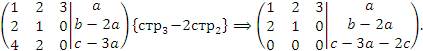 Если
Если 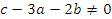 , то система является несовместной. В противном случае одна из неизвестных является свободной переменной и, следовательно, система имеет бесконечное множество решений. , то система является несовместной. В противном случае одна из неизвестных является свободной переменной и, следовательно, система имеет бесконечное множество решений.
|
***
2. Система линейных уравнений задана расширенной матрицей, представленной в приведенно-ступенчатой форме:
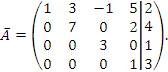 Выяснить сколько решений имеет эта система. Решение. Очевидно, что ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы и совпадает с числом неизвестных. Следовательно, система уравнений имеет единственное решение – согласно следствию из обобщенного правила Крамера.
Выяснить сколько решений имеет эта система. Решение. Очевидно, что ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы и совпадает с числом неизвестных. Следовательно, система уравнений имеет единственное решение – согласно следствию из обобщенного правила Крамера.
|
***
3. Выяснить сколько решений имеет система линейных уравнений, заданная расширенной матрицей
 при различных значениях параметра a. Решение. Если
при различных значениях параметра a. Решение. Если 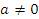 , то , то 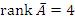 , тогда как , тогда как 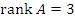 . В этом случае система является несовместной и не имеет решений.
Если a = 0, то . В этом случае система является несовместной и не имеет решений.
Если a = 0, то 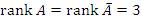 , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.
Следовательно, система имеет бесконечное множество решений. , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.
Следовательно, система имеет бесконечное множество решений.
|
Конспект лекций по дисциплине
«ОПЕРАЦИОННЫЕ СИСТЕМЫ»
Литература
1. Таненбаум Э., Вудхал А. Операционные системы. Разработка и реализация. 3-е изд. – СПб.: Питер, 2007. – 704 с.
2. Гордеев А.В. Операционные системы. – СПб.: Питер, 2007. – 416 с.
3. Гордеев А.В., Молчанов А.Ю. Системное программное обеспечение. – СПб.: Питер, 2002. – 736 с.
4. Харт Д.М. Системное программирование в среде Windows.: пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 529 с.
5. Гагарина Л.Г., Кокорева Е.В., Виснадул Б.Д. Технология разработки программного обеспечения. – М.: ИД «ФОРУМ»: ИНФРА-М, 2008. – 400 с.
6. Иртегов Д.В. Введение в операционные системы. – СПб.: БХВ-Петербург, 2002. – 624 с.
7. Олифер В.Г., Олифер Н.А. Сетевые операционные системы. – СПб.: Питер, 2001. – 544 с.
8. Партыка Т.Л., Попов И.И. Операционные системы, среды и оболочки. М.: ФОРУМ: ИНФРА-М, 2007. – 528 с.
9. Реймонд С. Искусство программирования для UNIX. – М.: Издательский дом «Вильямс», 2005. – 544 с.
Дата добавления: 2014-12-13; просмотров: 1049;
