ГЛОССАРИЙ. № Новые понятия Содержание Случайное событие событие, которое может произойти или не произойти в результате эксперимента
| № | Новые понятия | Содержание |
| Случайное событие | событие, которое может произойти или не произойти в результате эксперимента | |
| Элементарное событие | неразложимое случайное событие | |
| Достоверное событие Е | событие, которое обязательно произойдет в результате эксперимента | |
| Невозможное событие | событие, которое в данном опыте произойти не может | |
| Объединение (сумма) двух событий А и В | событие, состоящее из точек, принадлежащих или А или В, или обоим вместе. А ÈВ (А+В) | |
| Пересечение (произведение) двух событий А и В | событие, состоящее из точек, принадлежащих и А и В (обоим вместе). 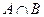 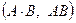
| |
| Разность двух событий А и В | событие, состоящее из точек, принадлежащих А, но не принадлежащих В. А / В (А − В) | |
| Противоположное событие | Событие, состоящее из точек пространства элементарных событий, не принадлежащих А. 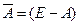
| |
| Несовместные события А и В | Пересечение событий А и В – пустое множество.
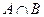 =Æ =Æ
| |
| Теорема сложения | 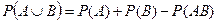
| |
Число размещений из n
по 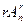
| 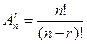
| |
| Число перестановок из n элементов | n! = n∙(n – 1) ∙(n – 2)…2∙1; 0! = 1; 1! = 1; 2! = 2; 3! = 6; 4! = 24; 5! = 120; …; (n + 1)! = (n + 1) ∙ n! | |
| Число сочетаний из n по k | 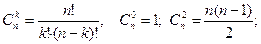
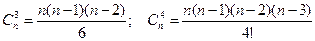
| |
| Формула условной вероятности | 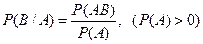
| |
| Теорема умножения вероятностей | P(AB) = P(A)∙P(B/A) = P(B)∙P(A/B) | |
| Независимые события А и В | Если Р(АВ) = Р(А)∙Р(В) | |
Полная группа событий
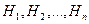
| 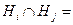 Æ для Æ для 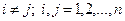
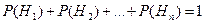
| |
| Формула полной вероятности | 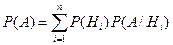
| |
Формула Байеса
(если 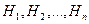 − полная
группа событий) − полная
группа событий)
| 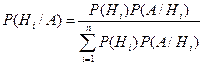
| |
| Дискретная случайная величина | случайная величина, возможные значения хi которой образуют конечное или счетное множество | |
| Закон распределения дискретной случайной величины | правило, по которому каждому возможному значению 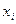  ставится в соответствие вероятность ставится в соответствие вероятность 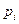 , с которой случайная величина принимает значение , с которой случайная величина принимает значение 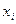 . . 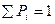
| |
Функция распределения 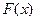 случайной величины x
случайной величины x
| 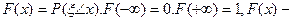 неубывающая функция неубывающая функция
| |
| Математическое ожидание | для дискретной случайной величины
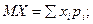 для непрерывной случайной величины
для непрерывной случайной величины
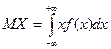
| |
| Дисперсия | Дискретной случайной величины
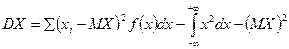
| |
| Биноминальное распределение | 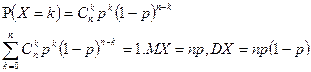
| |
| Распределение Пуассона | 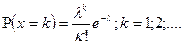
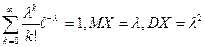
|
Тренинг умений
Дата добавления: 2014-11-30; просмотров: 2111;
