ПЕРЕЧЕНЬ УМЕНИЙ
Для заметок
Случайные события и их вероятности.
• Поля событий.
• Аксиомы теории вероятностей.
• Теорема сложения.
• Геометрические вероятности.
• Формула полной вероятности.
• Формула Байеса.
Дискретные случайные величины.
• Биномиальное распределение.
• Формула Бернулли.
• Распределение Пуассона.
• Математическое ожидание, дисперсия, среднеквадратическое отклонение.
ЛИТЕРАТУРА
1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. М.1989.
2. Гнеденко Б.В. Курс теории вероятностей. – М., 1988.
3. Феллер В. Введение в теорию вероятностей и ее приложения: В 2-х т. – М., 1984.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М., 1986
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М., 1998.
ПЕРЕЧЕНЬ УМЕНИЙ
| № | Умения | Алгоритмы |
Решения задач, когда все элементарные события равновероятны:
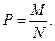
| 1. Подсчитывается количество всех элементарных событий N. 2. Подсчитывается количество всех благоприятных элементарных событий М. 3. М делится на N. | |
Подсчет геометрических вероятностей:
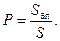
| 1. Вычисляется вся площадь S. 2. Вычисляется вся благоприятная площадь Sбл. 3. Sбл делится на S. | |
| Вероятности, связанные с подсчетом числа перестановок: N! = N(N – 1). . . 2∙1. | 1. Подсчитывается количество всех перестановок N!. 2. Подсчитывается количество всех благоприятных перестановок М. 3. М делится на N!. | |
Вероятности, связанные с подсчетом числа размещений:
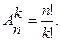
| 1. Подсчитывается количество всех размещений 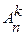 .
2. Подсчитывается количество всех благоприятных размещений М.
3. М делится на .
2. Подсчитывается количество всех благоприятных размещений М.
3. М делится на 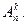
| |
Вероятности, связанные с подсчетом числа сочетаний:
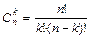
| 1. Подсчитывается количество всех сочетаний 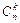 .
2. Подсчитывается количество всех благоприятных сочетаний М.
3. М делится на .
2. Подсчитывается количество всех благоприятных сочетаний М.
3. М делится на 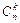 . .
| |
| Независимые события Р(АВ) = Р(А) ∙Р(В). | 1. Оцениваются вероятности событий 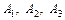 и их отрицаний и их отрицаний 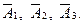 2. Пишутся, какие сочетания
2. Пишутся, какие сочетания 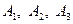 , , 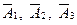 соответствуют оцениваемому событию.
3. Используется формула Р(АВ) = Р(А) ∙Р(В) для независимых событий. соответствуют оцениваемому событию.
3. Используется формула Р(АВ) = Р(А) ∙Р(В) для независимых событий.
| |
Формула полной вероятности:
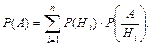
| 1. Выделяется полная группа событий 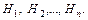 Подсчитываются вероятности Подсчитываются вероятности 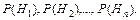
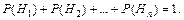 2. Подсчитываются условные вероятности
2. Подсчитываются условные вероятности 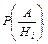 i = 1, 2, …, n
3. Значения P(Hi) и
i = 1, 2, …, n
3. Значения P(Hi) и 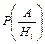 подставляются в формулу полной вероятности. подставляются в формулу полной вероятности.
| |
Формула Байеса:
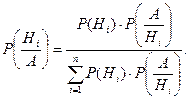
| 1. Выделяется полная группа событий 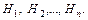 Подсчитываются вероятности Подсчитываются вероятности 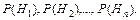
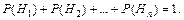 2. Подсчитываются условные вероятности
2. Подсчитываются условные вероятности 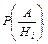 i = 1, 2, …, n
3. Значения P(Hi) и
i = 1, 2, …, n
3. Значения P(Hi) и 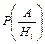 подставляются в формулу Байеса. подставляются в формулу Байеса.
| |
| Математическое ожидание МХ = mx, дисперсия DX, стандартное отклонение σ(х) дискретной случайной величины. | 1. Составляется таблица распределения дискретной случайной величины.
2. Подсчитывается математическое ожидание
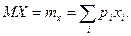 3. Подсчитывается дисперсия
3. Подсчитывается дисперсия 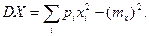 и
4. Подсчитывается стандартное отклонение σ(х) = и
4. Подсчитывается стандартное отклонение σ(х) = 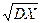 . .
| |
Биноминальное распределение:
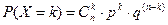
| 1.Подсчитываются нужные биноминальные коэффициенты 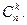 2.Значения
2.Значения 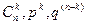 подставляются в формулу Бернулли. подставляются в формулу Бернулли.
| |
Распределение Пуассона:
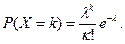
| 1.Определяется значение параметра λ распределения Пуассона.
2.Вероятности 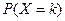 или берутся из таблицы, или подсчитываются самостоятельно. или берутся из таблицы, или подсчитываются самостоятельно.
| |
Математическое ожидание 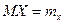 , дисперсия , дисперсия 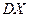 , стандартное отклонение , стандартное отклонение 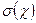 , вероятности , вероятности 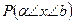 непрерывной случайной величины. непрерывной случайной величины.
| 1.Выписывается функция распределения 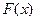 и плотность распределения и плотность распределения 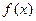 непрерывной случайной величины.
2.Подсчитывается математическое ожидание непрерывной случайной величины.
2.Подсчитывается математическое ожидание
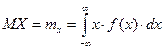 3.Подсчитывается дисперсия
3.Подсчитывается дисперсия 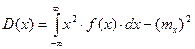 4.Подсчитаем стандартное отклонение
4.Подсчитаем стандартное отклонение 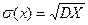 5.Подсчитаем
5.Подсчитаем 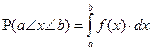 b b
|
Дата добавления: 2014-11-30; просмотров: 867;
