Моделирование в условиях противодействия, модели торгов
К этому классу относятся задачи анализа систем с противодействием (конкуренцией), также игровых по сути, но с одной особенностью — "правила игры" не постоянны в одном единственном пункте — цены за то, что продается.
При небольшом числе участников торгов вполне пригодны описанные выше приемы теории игр, но когда число участников велико и, что еще хуже, заранее неизвестно, — приходится использовать несколько иные методы моделирования ситуаций в торгах.
Наиболее часто встречаются два вида торгов:
· закрытые торги, в которых два или более участников независимо друг от друга предлагают цены (ставки) за тот или иной объект; при этом участник имеет право лишь на одну ставку, а ведущий торги принимает высшую (или низшую) из предложенных;
· открытые торги или аукционы, когда два или более участников подымают цены до тех пор, пока новой надбавки уже не предлагается.
Рассмотрим вначале простейший пример закрытых торгов. Пусть мы (A) и наш конкурент (B) участвуем в закрытых торгах по двум объектам суммарной стоимости C1 + C2.
Мы располагаем свободной суммой S и нам известно, что точно такой же суммой располагает наш конкурент. При этом S< C1 + C2, то есть купить оба объекта без торгов не удастся.
Мы должны назначить свои цены A1, A2 за первый и второй объекты в тайне от конкурента, который предложит за них же свои цены B1, B2.После оглашения цен объект достанется предложившему большую цену, а если они совпали — по жребию. Предположим, что и мы и наш конкурент владеем методом выбора наилучшей стратегии (имеем соответствующее образование).
Так вот — можно доказать, что при равных свободных суммах с нашей и с противоположной стороны существует одна, оптимальная для обеих сторон стратегия назначения цен.
Сущность ее (скажем, для нас) определяется из следующих рассуждений. Если нам удастся купить первый объект, то наш доход составит (C1 - A1)или же, при покупке второго, мы будем иметь доход (C2 - A2). Значит, в среднем мы можем ожидать прибыль
d = 0.5·(C1 + C2 — A1 — A2) = 0.5·(C1 + C2 — S). {3 - 17}
Таким образом, нам выгоднее всего назначить цены
A1 = C1 — d = 0.5 · (C1 — C2 + S);
A2 = C2 — d = 0.5 · (C2 — C1 + S).{3 - 18}
Если же одна из них по расчету окажется отрицательной — выставим ее нулевой и вложим все деньги в цену за другой объект.
Но и наш конкурент, имея ту же свободную сумму и рассуждая точно так же, назначит за объекты точно такие же цены. Как говорится, боевая ничья! Ну, если конкурент не владеет профессиональными
знаниями? Что ж, тем хуже для него — мы будем иметь доход больше, чем конкурент.
Конкретный пример. Сумма свободных средств составляет по 10000 гривен у каждого, цена первого объекта равна 7500, второго 10000 гривен.
Назначим цену за первый объект в 0.5·(7500-10000+10000)=3750 гривен, а за второй 0.5·(10000-7500+10000) = 6250 гривен.
Наш доход при выигрыше первого или второго объекта составит 3750 гривен. Такой же доход ожидает и конкурента, если он выбрал такую же, оптимальную стратегию. Но, если он так не поступил и назначил цену за первый объект 3500, а за второй 6000 гривен (пытаясь сэкономить!), то в таком случае мы можем выиграть торги по двум объектам сразу и будем иметь доход уже в 7500 гривен — приобретая имущество общей стоимостью в 17500 за цену в 10000 гривен!
Конечно, если стартовые суммы участников торгов неодинаковы, число объектов велико и велико число участников, то задача поиска оптимальной стратегии становится более сложной, но все же имеет аналитическое решение.
Рассмотрим теперь второй вид задачи — об открытых торгах (аукционах). Пусть все те же два объекта (с теми же стоимостями) продаются с аукциона, в котором участвуем мы и наш конкурент.
В отличие от первой задачи свободные суммы различны и составляют SA и SB , причем каждая из них меньше (C1 + C2)и, кроме того, отношение нашей суммы к сумме конкурента более 0.5, но менее 2.
Пусть мы знаем "толщину кошелька" конкурента и, поскольку ищем оптимальную стратегию для себя, нам безразлично — знает ли он то же о наших финансовых возможностях.
Задача наша заключается в том, что мы должны знать — когда надо прекратить подымать цену за первый объект. Эту задачу не решить, если мы не определим цель своего участия в аукционе (системный подход, напомним, требует этого).
Здесь возможны варианты:
· мы хотим иметь максимальный доход;
· мы стремимся минимизировать доход конкурента;
· мы желаем максимизировать разницу в доходах — свой побольше, а конкурента поменьше.
Наиболее интересен третий вариант ситуации — найти нашу стратегию, обеспечивающую
DA — DB =Max. {3-19}
Поскольку объектов всего два, то все решается в процессе торгов за первый объект. Будем рассматривать свой ход в ответ на очередное предложение цены Xза этот объект со стороны конкурента.
Мы можем использовать две стратегии поступить двумя способами:
· стремиться уступить первый объект конкуренту — за наибольшую цену, надеясь купить второй;
· стремиться купить первый объект — за минимальную цену, уступив конкуренту второй.
Пусть конкурент назначил за первый объект очередную сумму X.Если мы не добавим небольшую сумму (минимальную надбавку D), то первый объект достанется конкуренту. При этом у конкурента в запасе останется сумма SB - X. Доход конкурента составит при этом (без учета D) DB = С1 - X.
Мы наверняка купим второй объект, если у нас в кармане
SA = (SB - X) + D, то есть немного больше, чем осталось у конкурента.
Значит, мы будем иметь доход DA = C2 - (SB - X)и разность доходов в этом случае составит
DA - DB = C2 - C1 - SB + 2·X .{3-20}
Ясно, что эта разность будет положительна только тогда, когда мы уступим первый объект за цену
X > 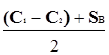 ,{3-21}
,{3-21}
но никак не меньше.
· Будем повышать цену за первый объект до суммы X+ Dс целью купить его.
Наш доход составит при этом
DA = C1 - (X + D).
Второй объект достанется конкуренту за сумму
SA - (X + D) + D,
так как ему придется поднять цену за этот объект до уровня, чуть большего остатка денег у нас.
Доход конкурента составит
DB = C2 - (SA - (X + D) + D),
а разность доходов составит (без учета D)
DA - DB = (C1 - X) - (C2 - SA + X) = С1 - С2 + SA - 2X .{3-22}
Эта разность будет положительна при условии
X < 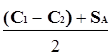 , {3-23}
, {3-23}
Мы нашли две "контрольные" суммы для того, чтобы знать — когда надо пользоваться одной из двух доступных нам стратегий — выражения {3-21} и {3-23}. Среднее этих величин составит
K = 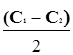 +
+ 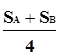 {3-24}
{3-24}
и определяет разумную границу для смены стратегий нашего участия в аукционе с целью одновременно получить доход себе побольше, а конкуренту — поменьше.
Интересно сосчитать свой доход и разность доходов на этой границе.
· Если мы уступили первый объект на этой границе, то по {3-20}
DA - DB = C2 - C1 - SB + 2K = 0.5(SA - SB).
· Если же мы купили первый объект на этой границе, то по {3-22}
DA - DB = С1 - С2 + SA - 2K = 0.5(SA - SB).
Для удобства сопровождения числовыми данными зададимся свободными суммами и ценами объектов (по нашему представлению об этих объектах): SA= 100 < 175; SB =110 < 175; C1 = 75; C2 = 100;
0.5 < (SA/ SB <2 и примем разрешенную надбавку к цене равной 1.
В этом конкретном случае граница "сражения" за первый объект проходит через сумму
K = 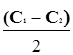 +
+ 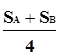 = -12.5 + 52.5 = 40 $
= -12.5 + 52.5 = 40 $
Если наш конкурент считает, что объекты для него стоят столько же (он знает нашу свободную сумму, а мы знаем его свободную сумму, но другой информации мы и он не обладаем), то он вычислит эту же границу и мы будем довольствоваться разностью доходов не в свою пользу: DA - DB = С1 - С2 + SA - 2K = 0.5(SA - SB) = -5.
Что делать — у конкурента больший стартовый капитал.
Но, возможно, наш конкурент (играя за себя) будет считать стоимости объектов совсем иными и для него граница будет совсем другой. Или же — цель конкурента в данном аукционе совершенно не такая как наша, что также обусловит другую граничную сумму участия в торгах за первый объект. Иными словами — оптимальная стратегия для конкурента нам совершенно неизвестна.
Тогда все зависит от того, на какой сумме он "отдаст" нам первый объект или, наоборот, до какой границы он будет "сражаться" за него . Следующая таблица иллюстрирует этот вывод.
Таблица 3.9
| Граница 1 торга за объект | Владелец 1 объекта | Доход DA | Доход DB | Разность DA - DB |
| A | ||||
| A | ||||
| A | ||||
| A | -5 | |||
| B | -5 | |||
| B | ||||
| B | ||||
| B | ||||
| B | ||||
| B |
Заканчивая вопрос об открытых торгах — аукционах, отметим, что в реальных условиях задача моделирования и выбора оптимальной стратегии поведения оказывается весьма сложной.
Дело не только в том, число объектов может быть намного больше двух, а что касается числа участников, то оно также может быть большим и даже не всегда известным заранее. Это приведет к чисто количественным трудностям при моделировании "вручную", но не играет особой роли при использовании компьютерных программ моделирования.
Дело в другом — большей частью ситуация усложняется неопределенностью, стохастичностью поведения наших конкурентов. Что ж, прийдется иметь дело не с самими величинами (заказываемыми ценами, доходами и т. д.), а с их математическими ожиданиями, вычисленными по вероятностным моделям, или со средними значениями, найденными по итогам наблюдений или статистических экспериментов.
Методы анализа больших систем, планирование экспериментов
Еще в начале рассмотрения вопросов о целях и методах системного анализа мы обнаружили ситуации, в которых нет возможности описать элемент системы, подсистему и систему в целом аналитически, используя системы уравнений или хотя бы неравенств.
Иными словами — мы не всегда можем построить чисто математическую модель на любом уровне — элемента системы, подсистемы или системы в целом.
Такие системы иногда очень метко называют "плохо организованными" или "слабо структурированными".
Так уж сложилось, что в течение почти 200 лет после Ньютона в науке считалось незыблемым положение о возможности "чистого" или однофакторного эксперимента. Предполагалось, что для выяснения зависимости величины Y=f(X) даже при очевидной зависимости Y от целого ряда других переменных всегда можно стабилизировать все переменные, кроме X, и найти "личное" влияние X на Y.
Лишь сравнительно недавно (см. работы В. В. Налимова) плохо организованные или, как их еще называют — большие системы вполне "законно" стали считаться особой средой, в которой неизвестными являются не то что связи внутри системы, но и самые элементарные процессы.
Анализ таких систем (в первую очередь социальных, а значит и экономических) возможен при единственном, научно обоснованном подходе — признании скрытых, неизвестных нам причин и законов процессов. Часто такие причины называют латентными факторами, а особые свойства процессов — латентными признаками.
Обнаружилась и считается также общепризнанной возможность анализа таких систем с использованием двух, принципиально различных подходов или методов.
· Первый из них может быть назван методом многомерного статистического анализа. Этот метод был обоснован и применен видным английским статистиком Р.Фишером в 20..30 годы этого столетия. Дальнейшее развитие многомерной математической статистики как науки и как основы многих практических приложений считается причинно связанным с появлением и совершенствованием компьютерной техники. Если в 30-е годы, при ручной обработке данных удавалось решать задачи с учетом 2..3 независимых переменных, то 1965 году решались задачи с 6 переменными, а к 70..80 годам их число уже приближалось к 100.
· Второй метод принято называть кибернетическим или "винеровским", связывая его название с отцом кибернетики Н.Винером. Краткая сущность этого метода — чисто логический анализ процесса управления большими системами. Рождение этого метода было вполне естественным — коль скоро мы признаем существование плохо организованных систем, то логично ставить вопрос о поиске методов и средств управления ими. Совершенно нелепо ставить вопрос о распределении токов в электрической цепи — это процессы в хорошо организованной (законами природы) системе.
Интересно, что оба метода, несмотря на совершенное различие между собой, могут применяться и с успехом применяются при системном анализе одних и тех же систем.
Так, например, интеллектуальная деятельность человека изучается "фишеровским" методом — многие психологи, как иронически замечает В.В.Налимов, "уверены, что им удастся разобраться в результатах многочисленных тестовых испытаний ".
С другой стороны, построение т.н. систем искусственного интеллекта представляет собой попытки создания компьютерных программ, имитирующих поведение человека в области умственной деятельности, т.е. применение "винеровского" метода.
Нетрудно понять, что экономические системы, скорее всего, следует отнести именно к плохо организованным — прежде всего, потому, что одним из видов элементов в них является человек. А раз так, то неудивительно, что при системном анализе в экономике потребуется "натурный" эксперимент.
В простейшем случае речь может идти о некотором элементе экономической системы, о котором нам известны лишь внешние воздействия (что нужно для нормального функционирования элемента) и выходные его реакции (что должен "делать" этот элемент).
В каком то смысле спасительной является идея рассмотрения такого элемента как "черного ящика". Используя эту идею, мы признаемся, что не в состоянии проследить процессы внутри элемента и надеемся построить его модель без таких знаний.
Напомним классический пример — незнание процессов пищеварения в организме человека не мешает нам организовывать свое питание по "входу" (потребляемые продукты, режим питания и т. д.) с учетом "выходных" показателей (веса тела, самочувствия и других).
Так вот, наши намерения вполне конкретны в части "что делать" — мы собираемся подавать на вход элемента разные внешние, управляющие воздействия и измерять его реакции на эти воздействия.
Теперь надо столь же четко решить — а зачем мы это будем делать, что мы надеемся получить. Вопрос этот непростой — очень редко можно позволить себе просто удовлетворить свою любознательность. Как правило, эксперименты над реальной экономической системой являются вынужденной процедурой, связанной с определенными затратами на сам эксперимент и, кроме того, с риском непоправимых отрицательных последствий.
Теоретическое обоснование и методика действий в таких ситуациях составляют предмет особой отрасли кибернетики — теории планирования эксперимента.
Договоримся о терминологии:
· все, что подается на вход элемента, будем называть управляющими воздействиями или просто воздействиями;
· все, что получается на выходе элемента, будем называть реакциями;
· если мы можем выделить в системе (или подсистеме) несколько в некотором смысле однотипных элементов, то их совокупность будем называть блоком;
· содержательное описание своих действий по отношению к элементам блока будем называть планом эксперимента.
Очень важно понять цель планируемого эксперимента. В конце концов, мы можем и не получить никакой информации о сущности процессов в цепочке "вход-выход" в самом элементе.
Но если мы обнаружим полезность некоторых, доступных нам воздействий на элемент и убедимся в надежности полученных результатов, то достигнем главной цели эксперимента — отыскания опти-мальной стратегии управления элементом. Нетрудно сообразить, что понятие "управляющее воздействие" очень широко — от самых обычных приказов до подключения к элементу источников энергетического или информационного "питания".
Оказывается, что уже само составление плана эксперимента требует определенных познаний и некоторой квалификации.
Опыт доказывает целесообразность включения в план следующих четырех компонентов:
· Описание множества стратегий управления, из которого мы надеемся выбрать наилучшую.
· Спецификацию или детальное сравнительное описание элементовблока.
· Правила размещения стратегий на блоке элементов.
· Спецификацию выходных данных, позволяющих оценивать эффективность элементов.
Внимательное рассмотрение компонентов плана эксперимента позволяет заметить, что для его реализации требуются знания в раз-личных областях науки, даже если речь идет об экономической системе — той области, в которой вы приобретаете профессиональную подготовку. Так, при выборе управляющих воздействий не обойтись без минимальных знаний в области технологии (не всегда это — чистая экономика), очень часто нужны знания в области юридических законов, экологии. Для реализации третьего компонента совершенно необходимы знания в области математической статистики, так как при-ходится использовать понятия распределений случайных величин, их математических ожиданий и дисперсий. Вполне могут возникнуть ситуации, требующие применения непараметрических методов статистики.
Для демонстрации трудностей составления плана эксперимента и необходимости понимания методов использования результатов эксперимента, рассмотрим простейший пример.
Пусть мы занимаемся системным анализом фирмы, осуществляющей торговлю с помощью сети "фирменных" магазинов и имеем возможность наблюдать один и тот же выходной показатель элемента такой системы (например, дневную выручку магазина фирмы).
Естественным является стремление найти способ повышения этого показателя, а если таких способов окажется несколько — выбрать наилучший. Предположим, что в соответствии с первым пунктом правил планирования эксперимента, мы решили испытать четыре стратегии управления магазинами. Коль скоро такое решение принято, то неразумно ограничить эксперимент одним элементом, если их в системе достаточно много и у нас нет уверенности в "эквивалентности" условий работы всех магазинов фирмы.
Пусть мы имеем N магазинов — достаточно много, чтобы провести "массовый" эксперимент, но их нельзя отнести к одному и тому же типу. Например, мы можем различать четыре типа магазинов: А, Б, В и Г (аптечные, бакалейные, водочные и галантерейные).
Ясно также (хотя и для этого надо немножко разбираться в технологии торговли), что выручка магазина вполне может существенно зависеть от дня недели — пусть рабочие дни всех магазинов: Ср, Пт, Сб, Вс.
Первое, "простое" решение, которое приходит в голову — выбрать из N несколько магазинов наугад (применив равновероятное распределение их номеров) и применять некоторое время новую стратегию управления ими. Но столь же простые рассуждения приводят к мысли, что это будет не лучшее решение.
В самом деле — мы рассматриваем элементы системы как "равноправные" по нескольким показателям:
· мы ищем единую и наилучшую для фирмы в целом стратегию управления;
· мы используем единый для всех элементов показатель эффективности (дневную выручку).
И, в то же время, мы сами разделили объекты на группы и тем самым признаем различие во внешних условиях работы для различных групп. На языке ТССА это означает, что профессиональные знания в области управления торговлей помогают нам предположить наличие, по крайней мере, двух причин или факторов, от которых может зависеть выручка: профиль товаров магазина и день недели. Ни то, ни другое не может быть стабилизировано — иначе мы будем искать нечто другое: стратегию для управления только водочными магазинами и только по пятницам! А наша задача — поиск стратегии управления всеми магазинами и по любым дням их работы.
Хотелось бы решить эту задачу так: выбирать случайно как группы магазинов, так и дни недели, но иметь гарантию (уже не случайно!) представительности выходных данных испытания стратегии.
Теория планирования эксперимента предлагает особый метод решения этой проблемы, метод обеспечения случайности или рандомизации плана эксперимента. Этот метод основан на построении
специальной таблицы, которую принято называть латинским квадратом, если число факторов равно двум.
Для нашего примера, с числом стратегий 4, латинский квадрат может иметь вид табл. 3.10 или табл. 3.11.
Таблица 3.10 Таблица 3.11
| Ср | А | Б | В | Г |
| Пт | В | Г | А | Б |
| Сб | Б | А | Г | В |
| Вс | Г | В | Б | А |
| Ср | Пт | Сб | Вс | |
| А | ||||
| Б | ||||
| В | ||||
| Г |
В ячейках первой таблицы указаны номера стратегий для дней недели и магазинов данного профиля, причем такой план эксперимента гарантирует проверку каждой из стратегий в каждом профиле торговли и в каждый день работы магазина.
Конечно же, таких таблиц (квадратов) можно построить не одну — правила комбинаторики позволяют найти полное число латинских квадратов типа "4·4" и это число составляет 576. Для квадрата "3·3" имеется всего 12 вариантов, для квадрата "5·5" — уже 161 280 вариантов.
В общем случае, при наличии t стратегий и двух факторах, определяющих эффективность, потребуется N=a·t2 элементов для реализации плана эксперимента, где aв простейшем случае равно 1.
Это означает, что для нашего примера необходимо использовать 16 "управляемых" магазинов, так как данные, скажем второй строки и третьего столбца, нашего латинского квадрата означают, что по субботам в одном из выбранных наугад бакалейных магазинов будет применяться стратегия номер 1.
Отметим, что латинский квадрат для нашего примера может быть помтроен совершенно иначе — в виде таблицы 3.11, но по-прежнему будет определять все тот же, рандомизированный план эксперимента.
Пусть мы провели эксперимент и получили его результаты в виде следующей таблицы, в ячейках которой указаны стратегии и результаты их применения в виде сумм дневной выручки:
Таблица 3.12
| Дни | Магазины А Б В Г | Сумма | |||
| Вс | 2: 47 | 1: 90 | 3: 79 | 4: 50 | |
| Ср | 4: 46 | 3: 74 | 2: 63 | 1: 69 | |
| Пт | 1: 62 | 2: 61 | 4: 58 | 3: 66 | |
| Сб | 3: 76 | 4: 63 | 1: 87 | 2: 59 | |
| Сумма | |||||
| Итого по стратегиям | 1050/4= 262.5 |
Если вычислить, как и положено, средние значения, дисперсии и среднеквадратичные отклонения для четверок значений дневной выручки (по дням, магазинам и стратегиям), то мы будем иметь следующие данные:
Таблица 3.12А
| Дни недели | Магазины | Стратегии | |
| Среднее | 262.5 | 262.5 | 262.5 |
| Дисперсия | 217.3 | 646.3 | 1563.3 |
| СКО | 14.74 | 25.42 | 39.5 |
| Коэф.вариации | 0.056 | 0.097 | 0.151 |
Уже такая примитивная статистическая обработка данных эксперимента позволяет сделать ряд важных выводов:
· сравнительно малые значения рассеяния данных по дням недели и по категориям магазинов в какой то мере вселяют надежду на правильный выбор плана эксперимента;
· разброс значений по стратегиям на этом фоне, скорее всего свидетельствует о большей зависимости дневной выручки от стратегии, чем от дней недели или категории магазина;
· заметное отличие средних по 1-й и 3-й стратегиям от средних по 2-й и 4-й, может быть основой для принятия решения — искать наилучшую стратегию, выбирая между 1-й и 3-й.
В этом — прямой практический результат использования рандомизированного плана, построения латинского квадрата.
Но это далеко не все. Теория планирования эксперимента дает, кроме способов построения планов с учетом возможных влияний на интересующую нас величину других факторов, еще и особые методы обработки полученных экспериментальных данных.
Самая суть этих методов может быть представлена так.
Пусть Wis есть выручка в i-м магазине при применении к нему s-й стратегии управления. Предполагается рассматривать эту выручку в виде суммы составляющих
Wis = W0 + Ds + ei;{3-25}
где:
· W0 определяет среднюю выручку для всех магазинов при условии применения к каждому из них всехстратегий по очереди с соблюдением постоянными всех других условий, влияющих на выручку;
· W0 + Ds есть средняя выручка при применении ко всем магазинам s-й стратегии;
· ei рассматривается как "ошибка измерения" — случайная величина с нулевым математическим ожиданием и нормальным законом распределения.
Несмотря на явную нереальность соблюдения постоянными внешних влияющих факторов, мы можем получить оценку каждого из слагаемых Wis и искать оптимальную стратегию через прибавку от ее применения Ds с учетом ошибки наблюдения. Можно считать доказанной "нормальность" распределения величины ei и использовать "правило трех сигм" при принятии решений по итогам эксперимента.
Дата добавления: 2014-12-10; просмотров: 854;
