Показатели надежности неремонтируемых объектов
Неремонтируемые объекты работают до первого отказа. Различные показатели надежности неремонтируемых объектов являются характеристиками случайной величины Т— наработки объекта до отказа.
Наработкой называется продолжительность или объем работы изделия, измеряемые в часах, километрах, циклах или в других единицах.
Функцией ненадежности случайной величины Т (или функцией распределения) называют вероятность того, что наработка до отказа Т меньше заданной наработки t, причем эта вероятность рассматривается как функция t:
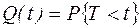 .
.
Часто применяют также функцию надежности
 .
.
Вероятностью безотказной работы называют вероятность того, что в заданном интервале времени или в пределах заданной наработки не возникнет отказ объекта.
Вероятность безотказной работы в течение интервала наработки (t1,t2) равна отношению значения функции надежности в конце интервала t2 к ее значению в начале интервала t1.
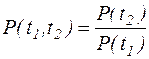 .
.
Плотностью распределения наработки до отказа называется производная от функции ненадежности
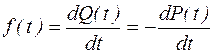 .
.
Величина f(t)dt характеризует вероятность того, что объект откажет на интервале (t, t+dt).
Интенсивностью отказов называется условная плотность вероятности возникновения отказа ремонтируемого объекта, определяемая для рассматриваемого момента наработки при условии, что до этого момента отказ не возник. Интенсивность отказов равна отношению
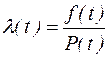 .
.
Величина 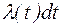 характеризует вероятность того, что объект откажет на интервале (t, t+dt) при условии, что он был работоспособен в начале интервала.
характеризует вероятность того, что объект откажет на интервале (t, t+dt) при условии, что он был работоспособен в начале интервала.
Из вышеизложенного имеем при Р(0)=1:
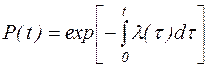 .
.
Условная вероятность безотказной работы в течение наработки (t1,t2), найденная в предположении, что при t1 объект был работоспособен,
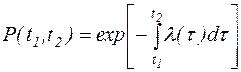 .
.
В качестве показателя надежности неремонтируемых объектов часто используется математическое ожидание наработки до отказа: средняя наработка до отказа
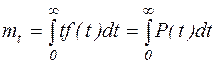 .
.
Тип распределения наработки до отказа зависит от особенностей процесса развития отказа.
Показательное (экспоненциальное) распределение применяется чаще других. Во-первых, оно характерно для сложных систем, состоящих из разнородных элементов с различными интенсивностями отказов. Во-вторых, при показательном распределении получаются относительно простые формулы для расчета надежности. Показательное распределение можно использовать в тех случаях, когда пренебрегают влиянием приработки, износа и старения.
Таблица 5.1 - Показатели надежности для показательного распределения.
| Плотность распределения | 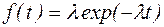
|
| Интенсивность отказов | 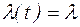
|
| Функция надежности | 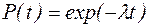
|
| Средняя наработка до отказа | 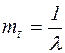
|
Дата добавления: 2014-12-09; просмотров: 2261;
