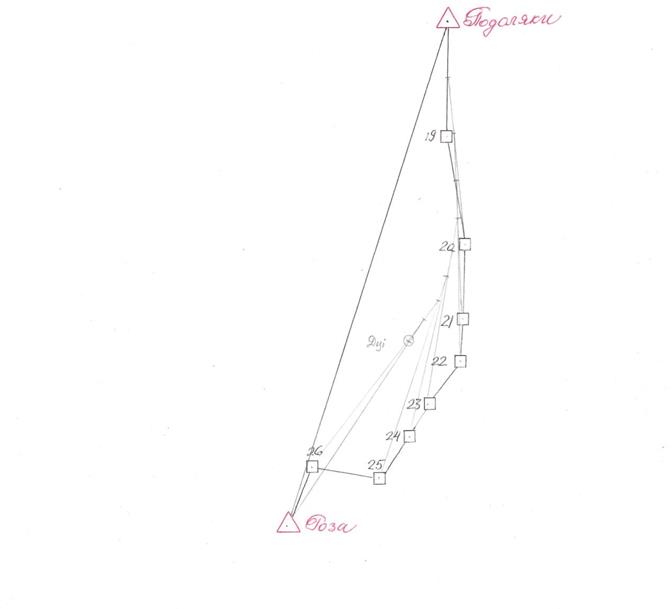
Приклад визначення центру тяжіння графічним методом.
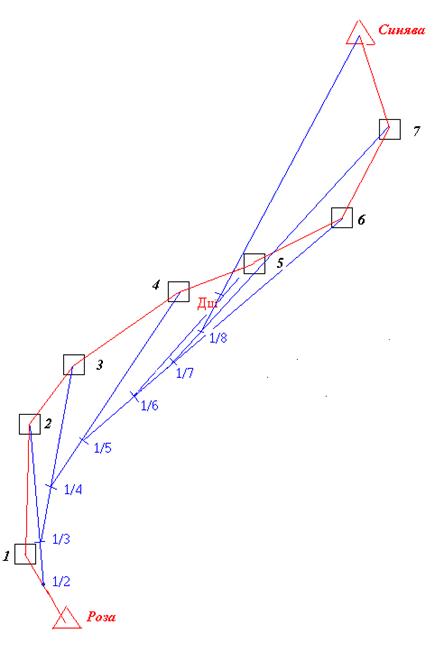
Від центру тяжіння виміряють відставні до кожної точки ходу і записують в таблицю.
|
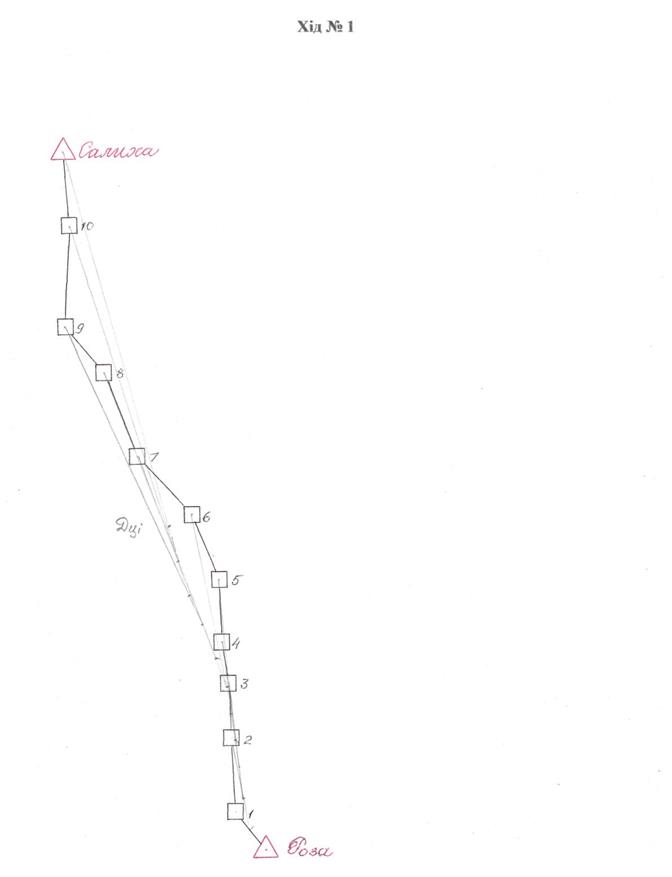
Хід № 1
| № точок | Відстань S до Дцї | S2 |
| Роза | ||
| Салиха | ||
| å |
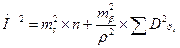 = 22´11+32² / 2062652 ´ 142257000 =44,03 см2
= 22´11+32² / 2062652 ´ 142257000 =44,03 см2
М=6,6 см
ms=2 см
n=11
mb= 3²
r = 206265²
Від центру тяжіння виміряють відставні до кожної точки ходу і записують в таблицю.
|
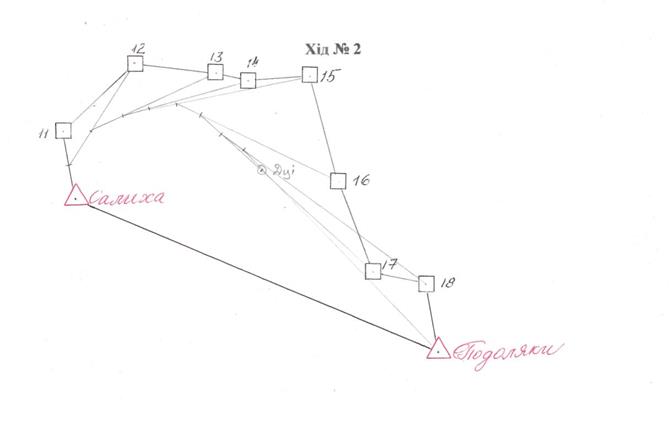
Хід № 2
| № точок | Відстань S до Дцї | S2 |
| Салиха | ||
| Подоляки | ||
| å |
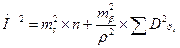 = 22´9+32² / 2062652 ´ 64059700 =36,01 см2
= 22´9+32² / 2062652 ´ 64059700 =36,01 см2
М=6,0 см
ms=2 см
n=9
mb= 3²
r = 206265²
Від центру тяжіння виміряють відставні до кожної точки ходу і записують в таблицю.
Хід № 3
|
Хід № 3
| № точок | Відстань S до Дцї | S2 |
| Подоляки | ||
| Роза | ||
| å |
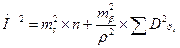 = 22´9+32² / 2062652 ´ 70478925 =36,01 см2
= 22´9+32² / 2062652 ´ 70478925 =36,01 см2
М=6,0 см
ms=2 см
n=9
mb= 3²
r = 206265²
Проектування нівелювання IV класу.
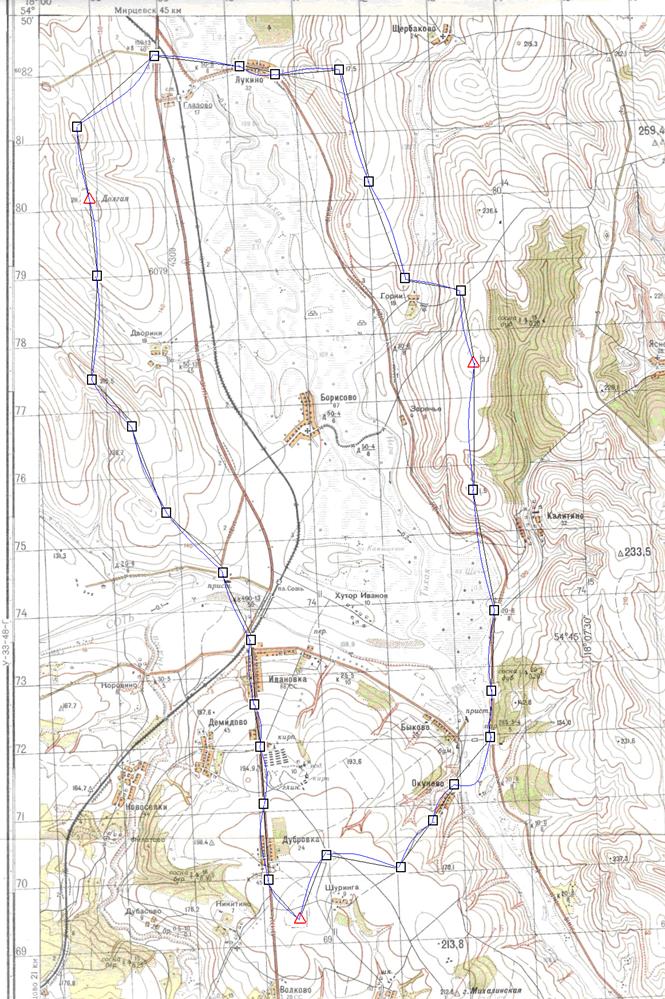
2. Висотні мережі:
Для оцінки точності нівелірних мереж знайдемо середню квадратичну помилку пункту, який розташований в середині ходу.
Середня квадратична помилка в середині ходу дорівнює:

З інструкції ми знаємо, що середня помилка відрізняється від середньої квадратичної помили на 1.4, тобто:  . Звідси
. Звідси  Q =
Q = 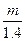 .
.
До висотного обґрунтування при створенні карт висуваються вимоги щоб середня квадратична помилка висот пунктів відносно вихідних пунктів не перевищувала 1/10 перерізу рельєфу. Висота перерізу рельєфу для нашої карти – 0,5 м.
Визначимо середню квадратичну помилку для всіх ходів.
Хід 1.
 =
= 
 Q =
Q = 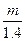 = 47,5/1,4=33,9 мм.
= 47,5/1,4=33,9 мм.
Допустиме значення Q = 0,5м/10 = 50 мм.
В нашому випадку в допуску.
Хід 2.
 =
= 
 Q =
Q = 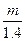 = 45,8/1,4=32,7 мм.
= 45,8/1,4=32,7 мм.
В нашому випадку в допуску.
Хід 3.
 =
= 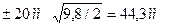
 Q =
Q = 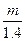 = 44,3/1,4=31,6 мм.
= 44,3/1,4=31,6 мм.
В нашому випадку в допуску.
Дата добавления: 2014-12-09; просмотров: 1085;
