Определение невыгоднейшего положения нагрузки на сооружении

Поскольку подвижную нагрузку можно рассматривать при некотором фиксированном положении, приведенные выше формулы для неподвижной нагрузки и в этом случае справедливы. Обычно при действии подвижной нагрузки ищут наибольшее или наименьшее значение усилия, следовательно, прежде чем пользоваться упомяну­тыми выше формулами, необходимо найти невыгодное (критическое) положение нагрузки.

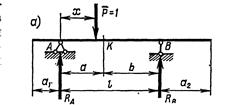
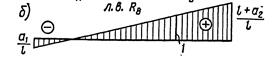1) Действие одной сосредоточенной силы Р. Рассмотрим определение по построенной выше линии влияния (см. рис. б) наибольшего и наименьшего значений реакции R_B (см. рис. а). Будем обозначать эти значения соответственно max R_bи min R_B. Очевидно, невыгоднейшим для сооружения положением подвижной силы Р будет точка С, поскольку этой точке соответствует наибольшая положительная ордината линии влияния R_B. Итак, maxR_B=(1+а₂/l)Р; min R_B = — а2/l P.

2) 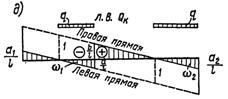Действие равномерно распределенной нагрузки постоянной ин­тенсивности, имеющей любые разрывы по направлению движения (нагрузки от толпы). Такая нагрузка встречается при расчете мостовых сооружений. Нетрудно догадаться, что наибольшее значение искомого усилия получим при одновременном нагружении всех положительных участков линии влияния, наименьшее значение — при нагружении отрицательных участков. Если обозначить через w₁ и w₂ площади отрицательных участков линии влияния Q_K (см. рис. д), min Qk — q (w₁ + w₂); q — интенсивность нагрузки, невыгодное положение которой показано над линией влияния.

3) Действие равномерно распределенной нагрузки постоянной интенсивности, имеющей заданные разрывы (нагрузки от колонны гусеничного или колесного транспорта). Невыгодное положение данной нагрузки характеризуется равенством сумм ординат линии влияния под левыми и под правыми краями нагрузки.

4) Действие системы связанных сосредоточенных грузов (давление осей локомотивов). Невыгодное (критическое) положение такой нагрузки над треугольной линией влияния характеризуется одновременным выполнением следующих двух неравенств:

(R_лев + Р_кр)/а ≥ R_пр/b; R_лев/a ≤ (Р_кр+R_пр)/b,

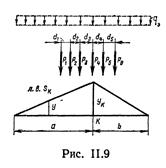где Р_кр — одна из сосредоточенных сил (см.рис.II.9), при расположении которой над вершиной линии влияния удовлетворяются оба неравенства; R_лев — равнодействующая сил, находящихся левее вершины; R_np — то же правее вершины. Одновременное удовлетворение обоих неравенств достигается путем нескольких попыток.

5)Эквивалентная нагрузка. Эквивалентной называется нагрузка, распределенная равномерно по всей длине линии влияния (см.рис. II.9) и вызывающая то же усилие, что и соответствующая система сосредоточенных грузов при их невыгодном расположении, т. е. Sk _max = q_эw, где w — площадь, ограниченная линией влияния:

w = Ук(а + b)/2.

При критическом положении сосредоточенных сил S_Kmax= ∑P_iy_i

Отсюда

q_э = ∑P_iy_i/w

Вычисленную по этой формуле q_э применяют для нагружения всех «подобных» линий влияния. Подобными называют треугольные линии влияния с одинаковыми значениями а и b ординаты их могут быть какими угодно.