Закон больших чисел Бернулли.

Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):

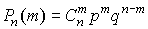
Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

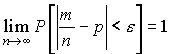
(55)

иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А).

Доказательство:

Рассмотрим случайную величину 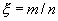. Так как M(m)=np и D(m)=npq (см. § 4, п. 2, пример 3), то

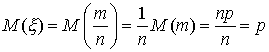
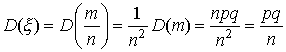
Применим к случайной величине вторую лемму Чебышева:

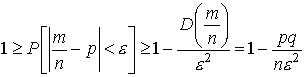
Переходя к пределу при , очевидно, имеем

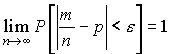
Мы говорили (см. § 1, п. 1), что при большом числе испытаний частота Р*(А)=m/n события А обладает свойством устойчивости. Это обстоятельство находит свое объяснение в законе больших чисел Бернулли.