Изменение тока при замыкании и размыкании цепи, содержащей индуктивность
При отсутствии индуктивности в цепи ток при замыкании и размыкании меняется практически мгновенно (рис. 1). Наличие в цепи индуктивности
| препятствует мгновенному изменению тока, так как согласно правилу Ленца эдс самоиндукции препятствует убыванию тока в цепи, которое и вызывает появление индукционного тока. Рассмотрим цепь, изображенную на рис. 2. При переводе ключа К из положения 2 в положение 1 ток в цепи начинает убывать, тогда по второму правилу Кирхгофа | 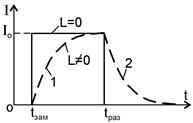 Рис. 1
Рис. 1
|
I×R = ec = - L× 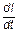 .
.
Имеем дифференциальное уравнение с разделяющимися переменными.
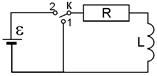 Рис. 2
Рис. 2
| Разделив переменные, получаем
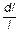 = - = - 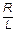 dt .
Интегрируя обе части уравнения, имеем
lnI = - dt .
Интегрируя обе части уравнения, имеем
lnI = - 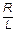 t + lnC1
или I = C1× t + lnC1
или I = C1× 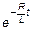 . .
|
Из начальных условий при t = 0 (в момент размыкания)I = Io = e/R, найдем величину C1 = Io.
Окончательно закон изменения тока при размыкании цепи принимает вид
I = Io× 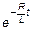 . .
| (5) |
Кривая зависимости тока от времени при размыкании цепи показана на рис. 1 пунктиром (кривая 2). Из формулы (5) следует, что чем больше индуктивность цепи, тем медленнее уменьшается ток в этой цепи, полностью исчезая за бесконечно большое время. Отсюда ясен физический смысл индуктивности: индуктивность цепи характеризует инертность цепи в электрических процессах.
Переведем ключ К в положение 2. Согласно второму правилу Кирхгофа в этом случае
I×R = e - L× 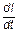 .
.
Перепишем это уравнение в виде
I×= 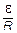 -
- 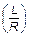 ×
× 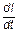 .
.
Так как 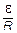 = Io - номинальное (установившееся) значение силы тока, то
= Io - номинальное (установившееся) значение силы тока, то
I×- Io = - 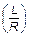 ×
× 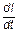 .
.
Так как d(I - Io) = dI, то
I×- Io = - 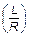 ×
× 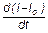
или
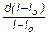 = -
= - 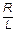 dt .
dt .
Интегрируя обе части уравнения, имеем
lnI = - 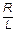 t + lnC1,
t + lnC1,
откуда после потенцирования получаем I- Io = C2× 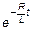 .
.
Из начальных условий при t = 0 (в момент замыкания)I = 0, найдем величину C2 = - Io, и тогда
I = Io×( 1 - 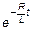 ). ).
| (6) |
График изменения тока при замыкании цепи изображен на рис. 1 пунктиром (кривая 1).
Из формул (5) и (6) следует, что длительность переходного процесса определяется отношением R/L , имеющим, размерность с-1. Обратная величина
t = L/R, (7)
имеющая размерность времени, также характеризует длительность переходного процесса и называется постоянной времени цепи. При t = 3t ток при замыкании цепи достигает 95% номинального значения, а при размыкании цепи ток не превышает 5% номинального значения. Из формулы (5) видно, что постоянная времени при размыкании цепи tр равна времени, в течение которого сила тока уменьшается в е раз, т.е. Itр » 0,37×Io. Постоянная времени призамыкании цепи tз согласно формуле (6) равна времени, в течение которого сила тока достигает значения Itз = (1 – e-1)×Io » 0,63×Io.
Если в результате эксперимента определить постоянную времени t как время, в течение которого сила тока достигает значения It, то при известном значении активного сопротивления цепи R индуктивность цепи можно рассчитать по формулам
L = tз×Rз, L = t р×Rр, (8)
где Rз и Rр - сопротивления цепи при замыкании и размыкании.
Дата добавления: 2014-12-06; просмотров: 6262;
