Явление самоиндукции
Электрический ток, текущий в проводящем контуре, создает потокосцепление
Y = N× 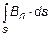 , ,
| (1) |
где Bn - проекция вектора магнитной индукции на нормаль к плоскости контура; S - площадь контура; N - число витков контура.
По закону Био-Савара-Лапласа магнитная индукция пропорциональна силе тока, создающего магнитное поле, т.е. B ~ I. Поэтому и потокосцепление в контуре также оказывается пропорциональным силе тока:
B ~ I или Y = L×I.
Коэффициент пропорциональности L между силой тока в контуре и полным магнитным потоком, пронизывающим этот контур, называется коэффициентом индуктивности или индуктивностью контура.
Так, для соленоида Bn = B = m×mo×n×I и
Y = m×mo× 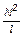 n×I×S = m×mo×n2×V×I, n×I×S = m×mo×n2×V×I,
| (2) |
где m - магнитная проницаемость среды; mо = магнитная постоянная; l, S, V – длина, площадь поперечного сечения и объем соленоида; n - число витков на единицу длины.
Индуктивность зависит только от размеров и формы контура, числа витков и магнитной проницаемости среды, в которой находится контур. Если магнитная проницаемость среды m не зависит от индукции магнитного поля, а следовательно, от тока в контуре, то L = const. Если внутри контура находится ферромагнитный сердечник, магнитная проницаемость которого m зависит от индукции намагничивающего поля, то индуктивность L ¹ const и зависит от индукции магнитного поля, а следовательно, от силы тока в контуре.
Единица индуктивности в СИ [ L ] = Гн .
При изменении силы тока в контуре изменяется пронизывающий контур магнитный поток. В результате в контуре возникает эдс самоиндукции, величина которой согласно закону Фарадея равна
ec = - 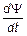 = - ( L× = - ( L× 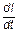 + I× + I× 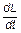 ). ).
| (3) |
В отсутствие ферромагнетиков L = const и 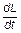 = 0, тогда
= 0, тогда
ec = - L× 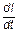 . .
| (4) |
Дата добавления: 2014-12-06; просмотров: 1277;
