Описание метода определения удельного заряда и экспериментальной установки
Для определения удельного заряда используются закономерности движения электронов в кольцевом пространстве между анодом 1 и катодом 2 двухэлектродной лампы, помещенной в магнитное поле (рис. 1). Напряженность электрического поля 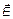 в лампе направлена по радиусу от анода к
в лампе направлена по радиусу от анода к
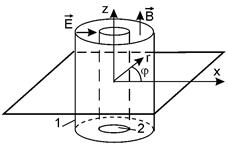 Рис. 1
Рис. 1
| катоду. Вектор индукции магнитного поля 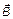 параллелен оси анода.
Рассмотрим движение электрона под действием электрического и магнитного полей, показанных на рис. 1. Траектории движения электронов представлены на рис. 2. При отсутствии магнитного поля траектория электрона прямолинейна и направлена вдоль радиуса от катода к параллелен оси анода.
Рассмотрим движение электрона под действием электрического и магнитного полей, показанных на рис. 1. Траектории движения электронов представлены на рис. 2. При отсутствии магнитного поля траектория электрона прямолинейна и направлена вдоль радиуса от катода к
|
аноду. При слабом магнитном поле траектория слегка искривляется под действием силы Лоренца, но электрон еще попадает на анод. Наконец, при В > Вкр
| электрон не достигает анода. Поэтому зависимость анодного тока от индукции магнитного поля должна иметь вид, показанный на рис. 3 пунктирной линией. Однако разброс начальных скоростей, некоторая несоосность катода и анода и другие причины приводят к тому, что эта зависимость имеет вид, показанный сплошной линией. Для описания движения электрона используем полярные координаты r, j (рис. 1). Начальной скоростью электронов пренебрегаем. | 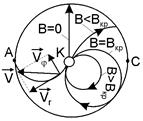 Рис. 2
Рис. 2
|
Работа электрического поля равна:
| A = e×Ua, | (1) |
где e - заряд электрона; Uа - анодное напряжение.
Магнитное поле работы не совершает, так как сила Лоренца перпендикулярна скорости электрона. Поэтому по закону сохранения энергия электрона равна работе сил электрического поля:
e×Ua= 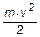 =
= 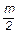 ×(Vr2 + Vj2), (2)
×(Vr2 + Vj2), (2)
где Vr и Vj - радиальная и угловая компоненты скорости электрона (рис. 2).
При В = Вкр, r = ra (точка С на рис. 2) Vr =0 траектория электрона касается
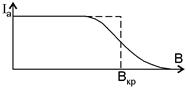 Рис. 3
Рис. 3
| анода, поэтому в этой точке
e×Ua= 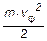 . (3) . (3)
|
Величину Vj = r×w найдем из уравнения движения электрона под действием силы Лоренца
Jz× 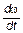 = Mz, = Mz,
| (4) |
где Mz - момент силы Лоренца относительно оси Z; Jz = m×r2- момент инерции электрона относительно оси Z. Величина момента силы Лоренца равна:
Mz = r×Fл = r× 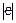 ×Vr×B = r× ×Vr×B = r× 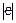 ×B× ×B× 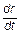 . .
| (5) |
Подставив величину Mz из уравнения (5) в уравнение (4) и интегрируя последнее, получаем
m×r2×w = 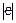 ×B× ×B× 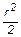 , ,
| (6) |
откуда
Vj = ×w×r = 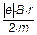 . .
| (7) |
Подставив Vj из уравнения (7) в уравнение (3) и решив полученное выражение относительно величины ( e/m ), получим
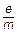 = = 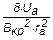 , ,
| (8) |
где ra - радиус анода; Ua - анодное напряжение; Вкр - критическое значение индукции магнитного поля, при котором начинается быстрый спад анодного тока (рис. 3).
Таким образом, для определения удельного заряда электрона необходимо по результатам эксперимента найти критическое значение индукции магнитного поля Вкр при заданноманодном напряжении Ua иизвестномрадиусе анода ra.
Электрическая схема экспериментальной установки приведена на рис. 4. Двухэлектродная лампа АК с цилиндрическим анодом радиусом ra = 5 мм помещена внутрь соленоида L. Лампа питается постоянным напряжением 24 В от щита питания лабораторного стола. Изменение анодного напряжения осуществляется реостатом R1, подключенным по схеме потенциометра. Ампервольтомметр (тестер) V и миллиамперметр mA служат для регистрации анодных напряжения и тока. Питание накала лампы осуществляется переменным напряжением 3 В от щита питания лабораторного стола. Цепь соленоида также питается постоянным напряжением 24 В. Изменение тока соленоида производится реостатом R2, подключенным по схеме переменного сопротивления. Регистрация тока соленоида Icoл осуществляется амперметром А.
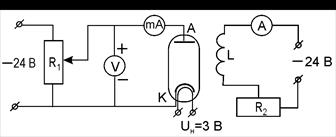
Рис. 4
Дата добавления: 2014-12-06; просмотров: 1327;
