I. ОПИСАНИЕ ПРЕДПРИЯТИЯ

Общая характеристика инфекционного процесса.

Инфекционные болезни - группа болезней, вызываемая микроорганизмами (вирусы, риккетсии, бактерии, одноклеточные паразиты)

Або

,

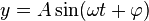4.Математичний маятник — тіло типу матеріальної точки, підвішене на довгій невагомій нерозтяжній нитці.
При відхиленні нитки від вертикального положення система нитка–тягарець може здійснювати коливання у вертикальній площині. Коливання відбуваються під дією повертаючої сили 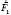, яка є складовою сили тяжіння 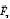.Період коливань математичного маятника .

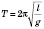Пружинний маятник складається з тягарця масою m, з’єднаного з пружиною жорсткістю k. Якщо зовнішньою силою вивести систему з положення рівноваги, вона може коливатися відносно положенняO.
Період коливань пружинного маятника .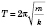

Коливання такого маятника відбувається під дією сили пружності, отже, на відміну від математичного, пружинний маятник може бути розташований і горизонтально. 

Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить черезцентр маси тіла.

Період коливань

,

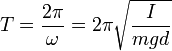5. Фізична величина 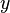, яка здійснює гармонічні коливання, задовольняє диференціальне рівняння

.

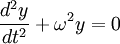У цьому випадку амплітуда коливань визначається початковими умовами.

Гармонічний осцилятор із частотою 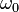може здійснювати гармонічні коливання на іншій частоті 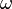під впливом зовнішньої дії з цією частотою. У такому випадку гармонічні коливання величини 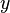задовольняє диференціальному рівнянню

.

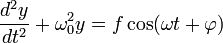6. Максимальне відхилення тіла, що коливається, від положення рівноваги називається амплітудою коливання тіла.
Час, протягом якого здійснюється одне повне коливання тіла, називається періодомколивання тіла Т.

Частота коливань f показує, яку кількість коливань тіло здійснює за одиницю часу.

Фаза — кількісна характеристика коливання, що визначає відмінність між двома подібними коливаннями, які починаються в різні моменти часу.

Циклічна частота— це кількість коливань за 2π секунд. Циклічна частота здебільшого позначається грецькою літерою ω.

7.

8. Метод векторних діаграм дає можливість замінити алгебраїчне додавання синусоїдальних величин геометричними діями над векторами відповідно до правил векторного аналізу.

Метод векторних діаграм полягає в наступному:

кожній синусоїдальній величині відповідає вектор цієї величини;

напрямок вектора синусоїдальної величини визначається початковою фазою;

модуль вектора синусоїдальної величини пропорційний діючому значенню або амплітуді цієї величини;

вектори синусоїдальних величин однакової кутової частоти можна складати геометрично як звичайні вектори.

Позитивний напрямок кута відлічується проти ходу годинної стрілки.

9. Кінетична енергія гармонічного осцилятора задається виразом

.

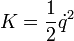Потенціальна енергія гармонічного осцилятора задається виразом

.

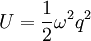Відповідно, вважаючи величину 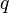узагальненою координатою, функція Лагранжа гармонічного осцлятора записується

.

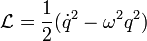Узагальнений імпульс

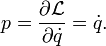
10. Додавання двох гармонійних коливань однакового напрямку й однакової частоти.

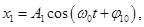
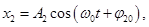
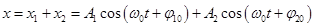
Результуючий вектор 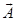рівний

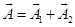
визначається за правилом паралелограма, його проекція на вісь X рівна

X=X₁ + X₂.

Довжина результуючого вектора або амплітуда результуючого коливання визначається по теоремі косинусів і рівна

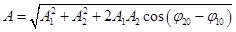
Початкова фаза результуючого коливання визначається з умови

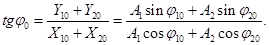
При додаванні двох гармонійних коливань із однаковою частотою й однакового напрямку результуючий рух є також гармонійним коливанням з тим же періодом і з амплітудою А, що лежить у межах

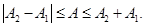
Коливання, у яких φ₁₀ = φ₂₀, А= А₁ + А₂називаються синфазними.

Коливання, у яких φ₁₀ - φ₂₀ = π, А=| А₂ – А₁|називаються протифазними.

У випадку, якщо А₁ = А₂, то при φ₁₀ = φ₂₀ А = 2А₁, при φ₁₀ - φ₂₀ = π, А=| А₂ – А₁| = 0.

11. Биття - додавання коливань із близькими частотами ω₁ ≈ ω₂.

При додаванні гармонійних коливань, що мало відрізняються по частоті, результуючий рух є гармонійним коливанням з пульсуючою амплітудою. Таке коливання називається биттями. Для простоти приймемо А= А₁ = А₂, φ₁₀ = φ₂₀ = 0.

Тоді

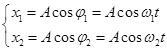
, где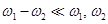

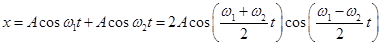(2)

Отримане вираження є добуток двох коливань.

Множник 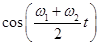має частоту середню для двох коливань, що складаються, т.т. близьку до їхніх частот ω₁ і ω₂. Другий множник 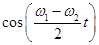має в силу умови близькості ω₁ і ω₂ малу частоту, тобто більший період. Це дозволяє розглядати результуючий рух як майже гармонійне коливання із середньою кутовою частотою 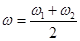й повільно мінливою амплітудою .

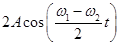Коли φ₁ ≈ φ₂, А_рез ≈ 2А. Через проміжок 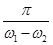, одне з коливань відстає від іншого по фазі на π і А_рез → 0 .Таке поступове зростання й убування амплітуд результуючого коливання називається биттям.

Якщо ω₁ і ω₂ порівнянні, тобто можна знайти два такі числа n₁ і n₂, що

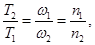то через проміжок часу 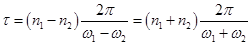аргументи обох співмножників в (2) зміняться на ціле ( хоча й різне ) число раз 2π, їхній добуток прийме теж значення, що й на початку проміжку τ. Величина τ тоді є періодом результуючого коливання.

Якщо частоти не порівнянні, то результуюче коливання буде неперіодичним.

12. Розглянемо результат додавання двох гармонійних коливань однакової частоти ω₁ = ω₂ = ω, що відбуваються у взаємно перпендикулярних напрямках уздовж осей х и y.

1. φ₂₀ - φ₁₀ = 2kπ;

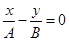
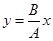
2. Δφ = (2k + 1)π;

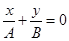
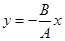
3. Δφ = ±π/2k;

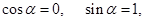
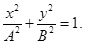
13.Згасаючі коливання — коливання, енергія яких зменшується з плином часу. Процес, що триває нескінченно, виду 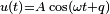в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найчастіше залежних лінійно від швидкості коливань 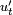або її квадрату.

Тому при виведенні рівняння гармонійних коливань з урахуванням енергетичних втрат у рівнянні (5) до повертаючої сили 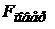треба додати ще 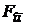, яка спрямована протилежно вектору швидкості:

.

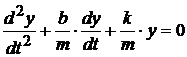Це рівняння називається диференціальним рівнянням затухаючих коливань. Його розв’язок, як відомо, має вигляд:

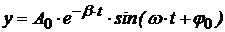
14.

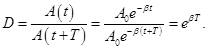
Логарифмічний декремент загасання дорівнює логарифму D:

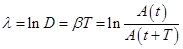
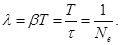
Логарифмічний декремент загасання обернено пропорційний числу коливань, у результаті яких амплітуда коливань поменшалася в е раз. Логарифмічний декремент загасання - постійна для даної системи величина.

Інтенсивність періодично змінюється , тому знайдемо середнє:(7), з врахуванням, що p=p0cosω0t . Тоді повна енергія, що випромінюється осцилятором за період буде:(8), p0=qpmax, і тоді закон зміни енергій осцилюючої системи: , де - логарифмічний декримент затухання. Отже, W=W0e-γt (10), де W0 – енергія осцилятора при t= 0. Енергія осцилятора зменшується по експоненційному закону . - час життя осцилятора.

Добротність коливальної системи,відношення енергії, запасеної в коливальній системі, до енергії, що втрачається системою за один період коливання. Добротність характеризує якість коливальної системи, тому що чим більше Д. к. с., тим менше втрати енергії в системі за одне коливання. Д. к. с. Q

15.

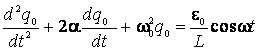(11),

яке і є диференціальним рівнянням вимушених коливань.

Як відомо, розв’язок його складається із суми розв’язків відповідного однорідного і частинного розв’язку неоднорідного рівняння. Розв’язок відповідного однорідного диференціального рівняння − це затухаючі коливання, які суттєво не впливають на загальний розв’язок. Тому частинний розв’язок можна шукати у загальному вигляді 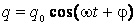(12). Знайшовши із (12)значення dq/dt та d²q/dt² та підставивши у (11) кінцево прийдемо до частинного розв’язку, який має вигляд

.

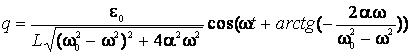З останнього виразу нескладно знайти закон зміни напруги на конденсаторі та закон зміни струму в коливальному контурі.

16. хвиля — процес розповсюдження коливань у будь-якому фізичному середовищі. Хвильовий процес — процес передачі коливань. При цьому частинки середовища не рухаються разом з хвилею, а коливаються навколо своїх положень рівноваги. Середовищем, у якому поширюються хвилі може бути як речовина, так і вакуум,

17. Поперечна хвиля - хвиля, в якій коливання відбуваються в площині, перпендикулярній до напрямку поширення. Хвиля, в якій коливання паралельні напрямку руху називається повздовжною.

Оскільки в площині існують два незалежні напрямки руху, то поперечні хвилі мають дві поляризації.

До поперечних хвиль належать електромагнітні хвилі у вакуумі.

Повздовжня хвиля - хвиля, в якій коливання в кожній точці простору паралельні напрямку розповсюдження. Хвиля, в якій коливання відбуваються в площині, перпендикулярній напрямку розповсюдження, називається поперечною.

В поздовжній електромагнітній хвилі вектор напруженості електричного поля направлений паралельно напрямку розповсюдження.

Прикладом поздовжніх хвиль є звукові хвилі в газі.

18.Довжина хвилі — характеристика плоскої періодичної хвилі, що позначає найменшу відстань між точками простору, в яких хвиля має однаковуфазу.

Довжина хвилі зазвичай позначається грецькою літерою λ.

19. Плоска́ хви́ля — хвиля, фронт якої є площиною. Рівняння плоскої хвилі має загальний вигляд:

,

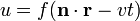де орт 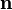задає напрям розповсюдження хвилі, v — швидкість хвилі, f — довільна функція.

Хвильовий вектор зазвичай позначається латинською літерою 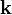й вимірюється в обернених сантиметрах.

Модуль хвильового вектора називається хвильовим числом.

Хвильове число зв'язане з довжиною хвилі λ співвідношенням:

.

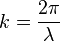20. Сфери́чна хви́ля — хвиля, яка розповсюджується від точкового джерела або збігається до нього.

Сферична хвиля у загальному випадку описується рівняннями

,

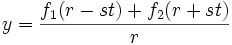де 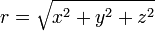— радіус, s — швидкість розповсюдження хвилі, 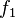та 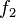— довільні функції, які задають форму хвилі. Перший доданок відповідає випадку, коли хвиля розбігається від джерела, другий — коли вона збігається до початку координат.

21. Хвильове́ рівня́ння — рівняння, яке описує розповсюдження хвиль у просторі.

Хвильове рівняння є зазвичай рівнянням другого порядку у часткових похідних гіперболічного типу, хоча існують хвильові рівняння інших порядків та інших типів.

У одновимірному випадку хвильове рівняння записується так:

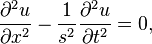
де u — невідома функція, яка описує хвилю, x — просторова координата, t — час, s — фазова швидкість поширення хвилі.

Загальний розв'язок хвильового рівняння подається суперпозицією функцій типу

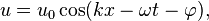
де 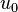— амплітуда хвилі, k — хвильове число, ω — циклічна частота, 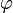— фаза хвилі.

Хвильове число та частота зв'язані між собою дисперсійним співвідношенням

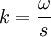
22. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результуюча амплітуда Авираховується за формулою:

,

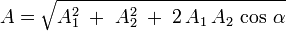де 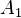та 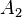— амплітуди відповідних хвиль, 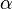— різниця фаз цих хвиль.

23. корельоване протікання в часі й у просторі декількох випадкових коливальних або хвильових процесів, яке дозволяє одержувати при їхньому додаванні чітку інтерференційну картину. Умовою когерентоності хвиль є незмінюваність у часі різниці між фазами коливань у них, що можливо лише тоді, коли хвилі мають однакову довжину (частоту).

Завдяки когерентності хвиль виникають інтерференційні явища.

24.

25.Стоя́ча— така хвиля, в якій будь-яка фаза коливань не поширюється в просторі. У випадку гармонічних коливань в одновимірному середовищі стояча хвиля описується формулою.

,

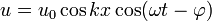де u — збурення в точці х в момент часу t, 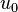— амплітуда стоячої хвилі, 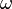— частота, k — хвильовий вектор, 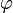— фаза.

Стоячі хвилі є розв'язками тих же хвильових рівнянь. Їх можна уявити собі, як суперпозицію хвиль, що розповсюджуються в протилежних напрямках.

I. ОПИСАНИЕ ПРЕДПРИЯТИЯ