Оценим с помощью средней ошибки аппроксимации качество уравнения.

Составим расчётную таблицу 3.

Таблица 4. 5. Расчётная таблица.

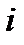
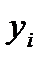
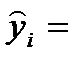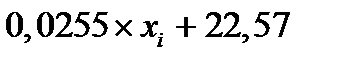
			Отклонение
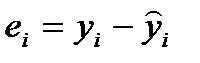
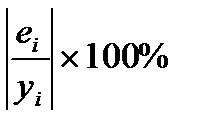
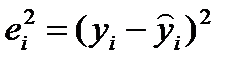
				3,98
				5,67
			-1	1,45
				18,43
			-26	27,19
				5,54
				2,56
				7,07
				1,44
				3,14
			-16	22,78
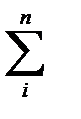
	1 097			99,25
				9,02

Определим среднюю относительную ошибку аппроксимации:

.

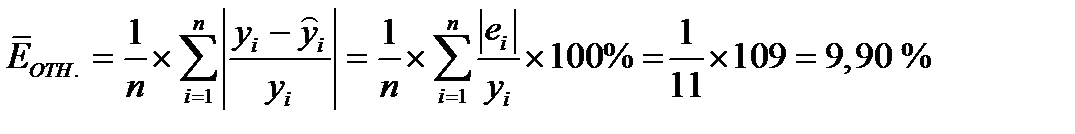В среднем расчётные значения 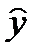для линейной модели отличаются от фактических значений на 9,90 %. «Хорошее» значение относительной ошибки аппроксимации лежит в пределах до 10 %.