Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

Оценку значимости уравнения регрессии проведём с помощью 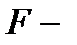критерий Фишера, для линейной модели справедливо соотношение:

.

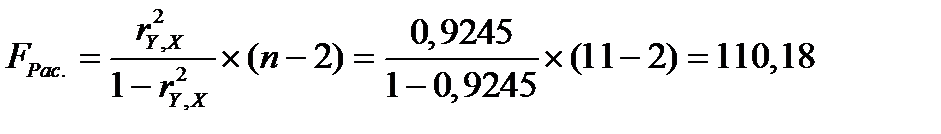Наблюдаемое значение 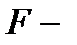критерий Фишера 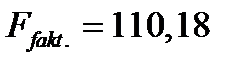больше табличного значения 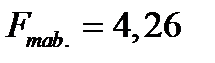для данного уровня значимости 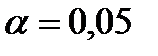и числа степеней свободы 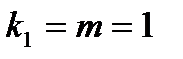и .

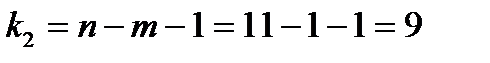Где 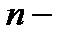число уровней ряда, 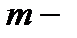количество параметров при неизвестных.

То есть,

.

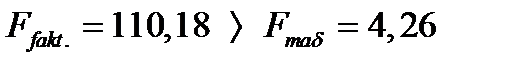Следовательно, уравнение регрессии с вероятностью 0,95 в целом статистически значимо.

Для основного теста на значимость находим расчётное значение 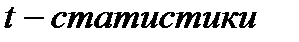Стьюдента:

,

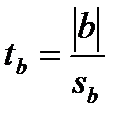где 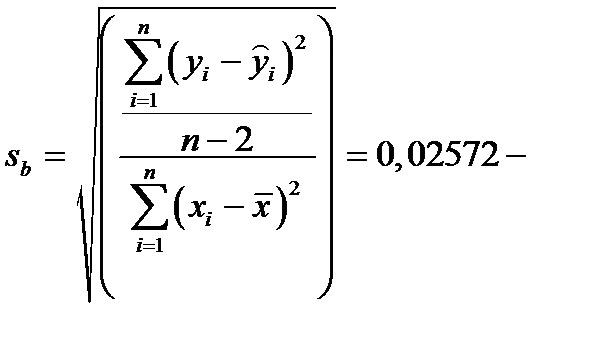стандартная ошибка коэффициента регрессии .

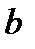Аналогично,

,

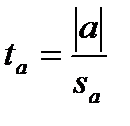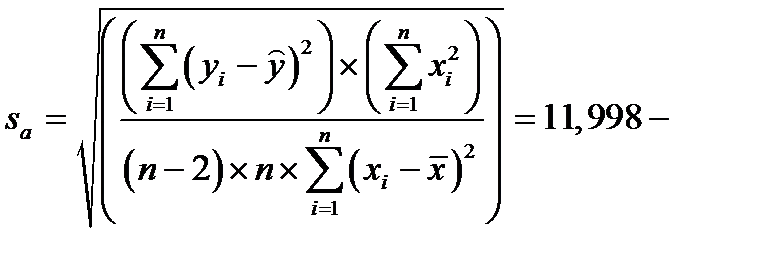стандартная ошибка коэффициента регрессии .

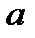Найденные значения 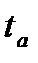и 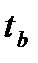сравним с табличным значением 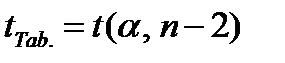, где 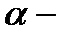уровень значимости, 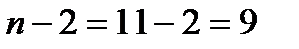число степеней свободы. В нашем случае имеем 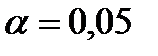. Тогда,

.

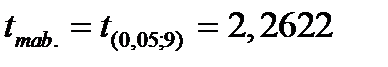Найдём стандартные ошибки для коэффициентов регрессии.

Выше нашли: .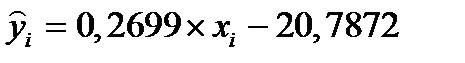

, .

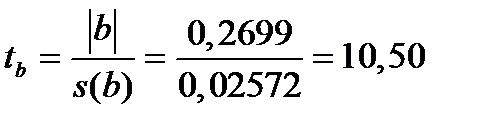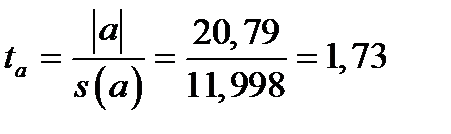Следовательно, (основной тест на значимость) с вероятностью 0,95

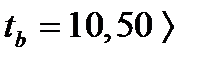
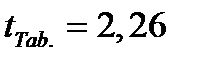, то параметр 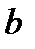статистически значим,

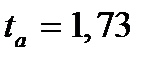
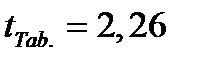, то параметр 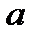статистически незначим.