ИДЗ-12. Решение задачи оптимизации.

Построить математическую модель и решить задачу оптимизации:

1.Полотняный шатер объемом V имеет форму прямого конуса. Каково должно быть отношение высоты конуса к радиусу его основания, чтобы на шатер пошло наименьшее количество полотна?

2.В равнобедренный треугольник с основанием a и углом при основании a вписать параллелограмм наибольшей площади так, чтобы одна из его сторон лежала на основании, а другая – на боковой стороне треугольника. Найти длины сторон параллелограмма.

3.Найти соотношение между радиусом R и высотой H цилиндра, имеющего при данном объеме V наименьшую полную поверхность.

4.Требуется сделать коническую воронку с образующей, равной 20 см. Какой должна быть высота воронки, чтобы ее объем был наибольшим?

5.Периметр равнобедренного треугольника равен 2p. Каково должно быть его основание, чтобы объем тела, образованного вращением этого треугольника вокруг его основания был наибольшим?

6.Найти высоту H конуса наибольшего объема, который можно вписать в шар радиуса R.

7.Проволокой, длина которой составляет l м, необходимо огородить клумбу, имеющую форму кругового сектора. Каким должен быть радиус круга R, чтобы площадь клумбы была наибольшей?

8.Определить наибольшую площадь S прямоугольника, вписанного в полукруг радиуса a.

9.Бревно длиной 20 м имеет форму усеченного конуса, диаметры оснований которого равны 2 м и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением и соосную с бревном так, чтобы ее объем был наибольшим. Каковы должны быть размеры балки?

10.С корабля, который стоит на якоре в 9 км от берега, нужно послать гонца в лагерь, расположенный на берегу в 15 км от ближайшей к кораблю точки берега. Скорость посыльного при движении пешком составляет 5 км/ч, а на лодке – 4 км/ч. В каком месте он должен пристать к берегу, чтобы попасть в лагерь в кратчайшее время?

11.Прямоугольная полоса жести шириной a = 0,5 м должна быть согнута в виде открытого кругового цилиндрического желоба так, чтобы его сечение имело форму сегмента. Каким должен быть центральный угол j, опирающийся на дугу этого сегмента, чтобы поперечное сечение желоба было наибольшим?

12.Из круглого цилиндрического бревна диаметром d надо вырезать балку прямоугольного сечения. Каковы должны быть ширина b и высота h этого сечения, чтобы балка, будучи горизонтально расположенной и равномерно нагруженной, имела наименьший прогиб? Известно, что величина прогиба обратно пропорциональна произведению ширины b поперечного сечения и куба его высоты h.

13.Рудное месторождение расположено на расстоянии 70 км от прямолинейной железной дороги. Расстояние по прямой от месторождения до перерабатывающего комбината равно 250 км. В каком месте надо начать строительство шоссе от железной дороги в направлении месторождения, чтобы обеспечить наименее затратную перевозку руды от месторождения к комбинату? Стоимость (в руб./кг×км) железнодорожной перевозки составляет 30 ед., по шоссе – 50 ед.

14.Туристу нужно добраться из пункта A, находящегося на одном берегу реки шириной h = 2 км, в пункт B, расположенный на другом берегу (расстояние между пунктами A и B (вдоль берега) равно a = 8 км). Скорость передвижения по берегу в k = 5 раз больше скорости передвижения по воде. Под каким углом туристу следует пересечь реку, чтобы добраться из A в B за минимальное время?

15.На прямолинейном отрезке AB длиной a, соединяющем два источника света A (силой p) и B (силой q) найти точку M, освещаемую слабее всего. Освещенность обратно пропорциональна квадрату расстояния от источника света.

16.Лампа висит над центром круглого стола радиусом r. При какой высоте лампы над столом освещенность предмета, лежащего на его крае, будет наилучшей? Освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света.

17.Из всех цилиндров, вписанных в данный конус, найти тот, у которого боковая поверхность наибольшая. Высота конуса H, радиус основания R.

18.Из бумажного круга вырезан сектор, а из оставшейся его части склеена коническая воронка. Какой угол должен иметь вырезанный сектор, чтобы объем воронки был наибольшим?

19.Из всех прямых конусов с данной боковой поверхностью S найти тот, у которого объем наибольший.

20.Сечение шлюзового канала имеет форму прямоугольника, заканчивающегося полукругом. Периметр сечения равен 45 м. При какой ширине канала его пропускная способность максимальна?

21.База находится в лесу в 5 км от дороги, а в 13 км от базы на этой дороге есть железнодорожная станция. Пешеход по дороге идет со скоростью 5 км/час, а по лесу – 3 км/час. За какое минимальное время пешеход сможет добраться от базы до станции?

22.Найти высоту h и радиус r основания прямого кругового конуса наименьшего объема, описанного около шара радиусом R.

23.При каком наклоне боковых сторон равнобедренной трапеции площадь ее будет наибольшей, если боковые стороны равны b, а меньшее основание равно a.

24.Из фигуры, ограниченной кривой y = 3 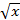и прямыми x = 4, y = 0, вырезать прямоугольник наибольшей площади.

25.Равнобедренный треугольник, вписанный в окружность радиусом R, вращается вокруг прямой, которая происходит через его вершину, параллельно основанию. Какой должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем?

26.Требуется изготовить открытый цилиндрический бак вместимостью V. Стоимость 1 м² материала из которого изготавливается дно бака, составляет P₁ = 300 руб., а стоимость 1 м², идущего на стенки бака, – P₂ = 200 руб. При каком отношении радиуса R дна к высоте H бака затраты на материал будут минимальными?

27.Сосуд с вертикальными стенками высотой H = 60 см, наполненный невязкой жидкостью, стоит на горизонтальной плоскости. Определить местоположение отверстия, при котором дальность струи будет наибольшей, если скорость вытекающей жидкости по закону Торричелли равна v = 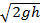, где h – высота столба жидкости над отверстием, g – ускорение свободного падения.

28.Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен 15 м. При каком радиуса полукруга R окно будет пропускать наибольшее количества света?

29.На странице книги печатный текст занимает площадь S = 300 см²; ширина верхнего и нижнего полей равна a = 20 мм, а правого и левого полей b = 15 мм. При каком отношении ширины к высоте текста площадь всей страницы будет наименьшей? Каковы при этом ее размеры?

30.Из круглого бревна, диаметр которого d, требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб? Сопротивление балки на изгиб Q пропорционально произведению ширины x ее поперечного сечения и квадрата его высоты y, т.е. Q = kxy², k = Const.

Литература

1. Берман Г.Н. Сборник задач по курсу математического анализа: учеб. пособие для вузов. СПб.: Лань, 2000. 448с.

2. Лунгу К.Н. и др. Сборник задач по высшей математике, М., Айрис Пресс, 2007, ч. 1, 2.

3. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-пресс. Ч.1: Тридцать шесть лекций. 2006, 288 с.

4. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-пресс. Ч.2: Тридцать пять лекций. 2006, 256 с.

5. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Е. Индивидуальные задания по высшей математике: учеб. пособие. Ч.1. Минск: Выш. шк., 2009. 304 с.

6. Фихтенгольц Г.М. Основы математического анализа: В 2 ч. СПб.: Лань. Ч.1. 2005. 448 с.

7. Фихтенгольц Г.М. Основы математического анализа: В 2 ч. СПб.: Лань. Ч.2. 2005. 464 с.