Определение количества групп

Количество групп (интервалов) вариационного ряда можно вычислить по формуле Стерджесса:

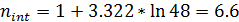(13)

Полученное значение округлим до ближайшего целого меньшего. Кроме того, желательно чтобы эмпирическое распределение было одномодальным, а частота каждого из интервалов была не меньше двух. С учётом изложенного, количество интервалов для рассматриваемого примера выбрано равным 5. Ширина интервала рассчитывается по формуле:

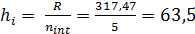(14)

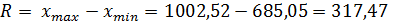где (15)

- размах вариации.

Для выполнения дальнейших расчетов, полученные результаты (интервалы и частоты) перепишем в табл. 2.

Таблица 2

Интервалы	Хgi	fi	φi	Σφi	Σygi	qi	Σqi	Σφi, %	Σqi, %	Σφi, %	fTi	φTi	ΣφTi	\|Σφi-ΣφTi\|	Ῡi	Дисп g	\|φ\|
685,05	748,54	716,80		0,229	0,229	162,460	0,162	0,162					0,166	0,166	0,064	14,769	2,948	7,298
748,54	812,04	780,29		0,271	0,500	242,620	0,242	0,404	22,92%	16,20%	22,92%		0,320	0,486	0,014	18,663	0,921	14,283
812,04	875,53	843,79		0,313	0,813	344,230	0,343	0,747	50,00%	40,39%	50,00%		0,315	0,801	0,012	22,949	1,681	14,030
875,53	939,03	907,28		0,125	0,938	156,500	0,156	0,903	81,25%	74,71%	81,25%		0,158	0,959	0,022	26,083	1,202	7,080
939,03	1002,52	970,77		0,063	1,000	97,120	0,097	1,000	93,75%	90,32%	93,75%		0,041	1,000	0,000	32,373	0,507	1,782
						1002,93			100,00%	100,00%	100,00%

где 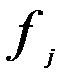- частота (число фирм) в интервале ;

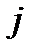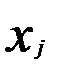- среднее значение стоимости активов в интервале ;

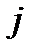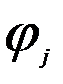- частость (доля банков) в интервале ;

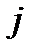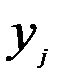- прибыль банков за квартал в 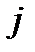- ой группе , млн. долл.;

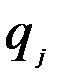- частость (доля) прибыли в интервале .

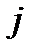В каждой выделенной группе различают нижнюю и верхнюю границы интервала. Так, в последней группе фирм по объёму ВТО нижняя граница —939,03, а верхняя — 1002,52 млн. долл.

Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Частоты ряда ( 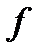) могут быть заменены частостями ( 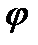), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму.

Диаграмма частот ряда распределения приведена на рис. 1.

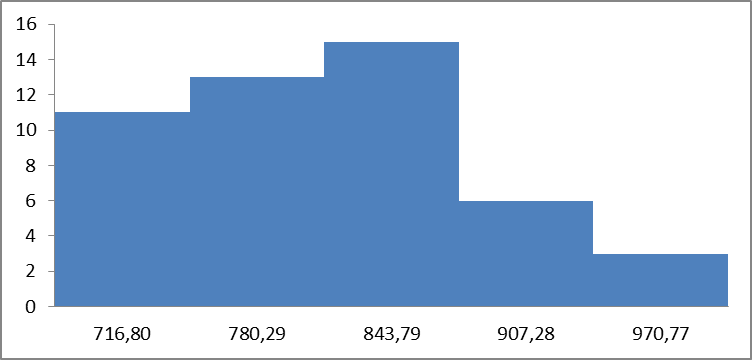
Рис.1 Диаграмма частот ряда распределения

<123 4 5 6 7 >

Дата добавления: 2014-11-29; просмотров: 1192;