Расчет будущей стоимости
Простой процент. Простым называется процент, который начисляется только на изначальную сумму инвестиций (кредита). По методике простого процента доход в денежном выражении определяется по формуле:
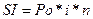 (1)
(1)
где SI - доход, рассчитанный по простому проценту, тыс. руб.; Ро — первоначальная (базовая, исходная) величина инвестиций (или принципал), тыс. руб.; i - процентная ставка (цена денег) за расчетный период, %; п — количество временных периодов, за которые начисляется простой процент на сумму первоначальной инвестиции.
Будущую стоимость (FV) денег первоначального вклада можно определить по формуле:
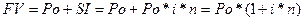 (2)
(2)
Расчет простых процентов используется в следующих операциях на практике:
- при оценке доходности депозитных вкладов с ежемесячной выплатой процентов;
- при оценке платы за пользование ресурсами при выдаче краткосрочных ссуд;
- в кредитных договорах с периодическим погашением основной суммы долга и выплатой процентов;
- при учете векселей;
- при оценке доходности дисконтных ценных бумаг;
- при расчете штрафных санкций за пользование чужими финансовыми ресурсами и пр.
Однако данный метод расчета доходов невыгодный. Начисленные процентные доходы также имеют стоимость, и инвестор вправе рассчитывать на дополнительную выгоду от того, что они находятся в обороте должника (дебитора, заемщика денег).
Формула простого процента может быть использована для расчета любого показателя в ее составе:
1. для расчета первоначальной суммы 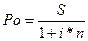
2. для расчета суммы процентных денег 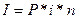
3. для расчета ставки процента 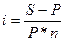
4. для расчета периода 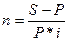
Сложный процент. В основе практически всех финансовых расчетов лежит метод начислений процентов на проценты, или принцип сложного процента. Математический аппарат сложных процентов используется в следующих расчетах:
- при депозитных договорах с капитализацией вкладов;
- при оценке доходности процентных ценных бумаг;
- при изучении эффективности финансовых инструментов;
- в инвестиционных расчетах при сопоставлении финансовых потоков, относящихся к различным временным периодам и в других аналогичных случаях.
Формула расчета будущей стоимости денег (в нашем примере это стоимость депозитного вклада) строится на основе известных параметров: первоначальной инвестиции (Ро), годовой ставки процента (i), количества лет (n). Сумма денег на депозите на конец первого года (FV1) определяется по формуле 2 при n= 1:
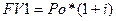
Для того чтобы рассчитать сумму денег на счете на конец второго года (FV2) по принципу сложного процента, в качестве базовой следует рассматривать уже не первоначальную инвестицию (Ро), а ту сумму, которая образовалась на счете в конце первого года, т.е. FV1:
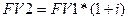 (3)
(3)
Перепишем эту формулу, подставив значение FV1, т.е. выразив FV2 через первоначальную инвестицию (Ро):
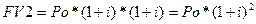 (4)
(4)
В универсальном виде для любых условий первоначальных инвестиций, процентных ставок и количества лет расчет будущей стоимости денег по методу сложного процента будет определяться по формуле:
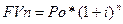 (5)
(5)
Если величина первоначальной инвестиции (Ро) может иметь практически бесконечное количество возможных значений, то второй сомножитель формулы 5 – (1+i)n , является величиной, которую для удобства вычислений можно стандартизировать. Для этого разработаны специальные таблицы с расчетом будущей стоимости 1 руб. при различных вариантах сочетания ставок процента и количества лет. Сокращенная версия приведена в таблице 1.
Расчет будущей стоимости 1 руб. при различных сочетаниях ставок процента и количества лет: (1+i)n = T1(i,n)
| Период | Ставка, % | |||
| 1,040 | 1,060 | 1,080 | 1,100 | |
| 1,082 | 1,124 | 1,166 | 1,210 | |
| 1,125 | 1,191 | 1,260 | 1,331 | |
| 1,170 | 1,263 | 1,361 | 1,464 |
В упрощенном варианте формулу расчета будущей стоимости с учетом значений таблицы записывают следующим образом:
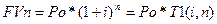 (6)
(6)
где Т1(i, n) — стоимость 1 руб. с начисленными сложными процентами при заданных значениях i и n, которые приведены в таблице.
Многие финансовые операции предполагают начисление сложных процентов чаще одного раза в год. Например, банки могут начислять проценты по кредитам поквартально или даже ежедневно. Для таких случаев будущая стоимость денежных поступлений рассчитывается по следующей формуле:
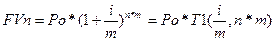 (7)
(7)
Формула расчета сложных процентов может быть использована для расчета любого входящего параметра:
1. первоначальная сумма 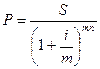
2. периода 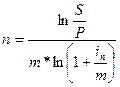
3. ставка процента 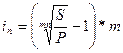
4. процентный доход 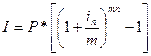
Будущая стоимость серийных платежей (аннуитетов). Широкое распространение в практике финансовых расчетов имеют серийные выплаты (или поступления) равновеликих сумм в течение фиксированных интервалов времени, иначе называемые аннуитетами. Примерами аннуитета является последовательность получения процентов по облигациям, платежи по потребительскому кредиту, выплаты страховых премий в рассрочку и пр. Аннуитеты различаются между собой следующими основными характеристиками:
- член аннуитета (А) - размер отдельного платежа;
- период аннуитета - временной интервал между двумя последовательными платежами;
- срок аннуитета (п) - время от начала первого периода ренты до конца последнего (или неогранченные во времени аннуитеты, т. н. «вечные»);
- процентная ставка ii), размер которой не всегда прямо оговаривается в условиях финансовой операции; однако этот параметр крайне необходим для ее анализа
- дополнительные условия и параметры, необходимые для характеристики некоторых видов аннуитетов (например, число платежей в году, способ и частота начислений процентов, параметры, характеризующие закономерность изменения размеров члена ренты во времени).
Наибольшее распространение на практике имею аннуитеты постнумерандо (обычные), когда суммы денежных средств вносятся в конце каждого периода.
Задачей финансовой математики является определение будущей стоимости серии равных периодических выплат (FVAn) в течение определенного временного периода (n) при заданной процентной ставке (i) по следующей формуле:
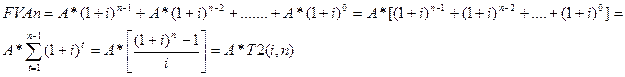 (8)
(8)
Где А — равновеликая сумма серийных платежей, тыс. руб.; Т2(i, n) — будущая стоимость серии равновеликих периодических выплат в размере 1 руб. в течение n количества периодов, исчисленная по i-й процентной ставке.
Сомножитель Т2(i, n) для удобства также стандартизирован в виде специальной таблицы 3.
Расчет будущей стоимости серии равновеликих периодических выплат в размере 1 руб. в течение n количества периодов при i-той процентной ставке. 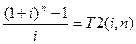
| Период | Ставка, % | |||
| 1,000 | 1,000 | 1,000 | 1,000 | |
| 2,040 | 2,060 | 2,080 | 2,100 | |
| 3,122 | 3,184 | 3,246 | 3,310 | |
| 4,247 | 4,375 | 4,506 | 4,641 |
Эффективная годовая процентная ставка.
В зависимости от особенностей финансовых инструментов и специфических договоренностей в финансовых контрактах могут предусматриваться различные схемы начисления процентов. Как правило, оговаривается номинальная годовая процентная ставка. Для того чтобы провести сравнительный анализ эффективности операций, необходимо определить универсальный показатель доходности для любой схемы начисления процентов. Таким показателем является эффективная годовая процентная ставка – которая измеряет реальный относительный доход, который получают в целом за год от финансовой операции при использовании данной схемы начисления.
Эффективная процентная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и м-разовое начисление процентов по номинальной ставке i.
Для определения эффективной ставки используется следующая формула:
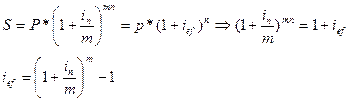
Сопоставление простых и сложных процентов осуществляется с помощью эффективной процентной ставки, эквивалентной для простой номинальной процентной ставки:
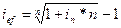
Ставка ief - является критерием эффективности финансовой сделки и может быть использована для пространственно-временных сопоставлений.
Дата добавления: 2014-12-05; просмотров: 3554;
