И конденсатор в цепи синусоидального тока

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.7.8). В схеме протекает синусоидальный ток

.

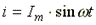Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,

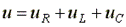
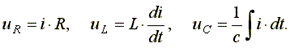(7.15)

Рис. 7.8

Подставим эти формулы в уравнение (7.15). Получим:

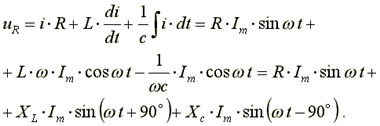(7.16)

Из выражения (7.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
Запишем уравнение (7.16) в комплексной форме:

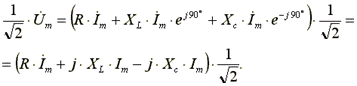(7.17)

Поделим левую и правую части уравнения (7.17) на √2.
Получим уравнение для комплексов действующих значений токов и напряжений

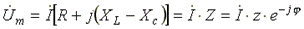, (7.18)

Где 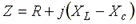- комплексное сопротивление цепи;
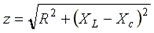- модуль комплексного сопротивления, или полное сопротивление цепи;
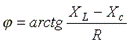- начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.7.9).

Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.7.10).

Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7.11).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

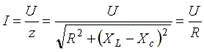
Условие возникновения резонанса:

,

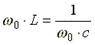отсюда резонансная частота равна

.

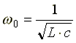Из формулы следует, что режима резонанса можно добиться следующими способами:

- изменением частоты;

- изменением индуктивности;

- изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

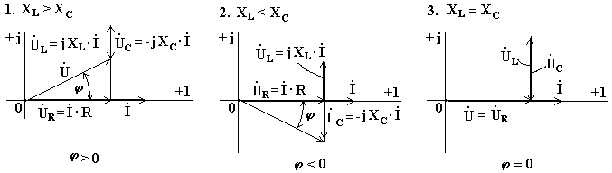
Рис. 7.9 Рис. 7.10 Рис. 7.11

7.8. Параллельно соединенные индуктивность, емкость
и активное сопротивление в цепи синусоидального тока

К схеме на рис. 7.12 подключено синусоидальное напряжение 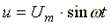. Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
Определим ток на входе схемы.

Рис. 7.12

В соответствии с первым законом Кирхгофа:

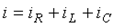, (7.19)

где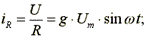
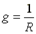- активная проводимость.

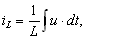
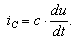
Подставим эти формулы в уравнение (7.19). Получим:

, (7.20)

Где 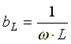- индуктивная проводимость;
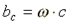- емкостная проводимость.

Из уравнения (7.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.
Запишем уравнение (6.20) в комплексной форме.

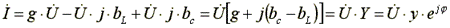, (7.21)

где 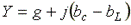- комплексная проводимость;
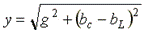- полная проводимость;
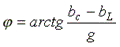- начальная фаза комплексной проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению (7.21).

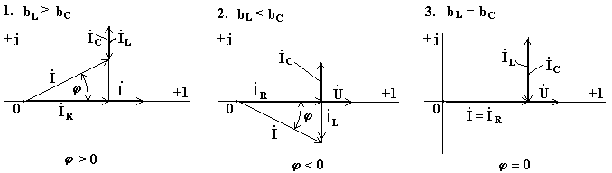
Рис. 7.13 Рис. 7.14 Рис. 7.15

В схеме на рис. 7.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
Из условия возникновения резонанса тока 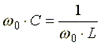получим формулу для резонансной частоты тока

.

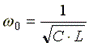В режиме резонанса тока полная проводимость цепи 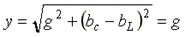- минимальна, а полное сопротивление 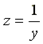- максимально. Ток в неразветвленной части схемы 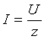в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

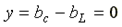и .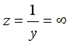

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.