Г. Киров
Термин «метафизический» Тейяр употребляет в смысле "стремящийся к познанию бытия с его принципами, началами, причинными механизмами и т. д.", в противоположность «феноменологическому», то есть ограничивающемуся описательными задачами. Метафизический подход, как его понимает Тейяр, отвечает на вопрос «почему», феноменологический — на вопрос «как». К отказу от «метафизики» Тейяр прибегает (прием, заимствованный у позитивистов) в случаях, когда стремится избежать обсуждения онтологических вопросов. На усмотрение читателя предоставляется выбор той или иной онтологии под «феноменалистскую» картину фактов (см. примеч. 15). При этом Тейяр допускает и антропоморфизацию, восходящий к средневековой и ренессансной (Парацельс) картине мира параллелизм между "феноменом человека" и "феноменом космоса" как между микрокосмом и макрокосмом. Еще в 1931 году Тейяр сформулировал свой "давно усмотренный" им принцип, что "только исходя из человека, может человек разгадать (dechiffrer) мир" (Р. Teilhard de Chardin. Images et paroles. Paris, 1966, p. 98). Декларируя феноменологичность своего метода, Тейяр тем не менее на деле (как естествоиспытатель) не может не использовать причинных объяснений. Так, он отнюдь не довольствуется «описанием» того факта, что около ископаемых останков синантропа найдены следы огня и обработанные орудия, но делает выводы о причине их появления: образе жизни и уровне организации синантропов (отвергая в то же время альтернативные причинные же объяснения: см. примеч. 20). Другим отступлением от феноменологичности служат нередкие у Тейяра, в особенности в последних разделах "феномена человека", причинные объяснения, исходящие из "внутреннего вещей" и "радиальной энергии". К тейяровскому «антиметафизическому» подходу применимо, таким образом, замечание Маркса (по поводу феноменологии Гегеля) о том, что в феноменологии в качестве возможности "уже заключен в скрытом виде… некритический позитивизм и столь же некритический идеализм" (К. Маркс и Ф. Энгельс. Соч., т. 42, с. 157). — Здесь и далее прим. переводчика.
(обратно)
Представление об атомизме Эпикура (341–270 гг. до н. э.), древнегреческого философа-материалиста, у Тейяра неточно. Эпикуровские атомы неделимы, как это предполагается и этимологией слова «атом», и как это мыслится у всех античных материалистов, но Эпикур не считает свои атомы инертными. Он ввел в учение об атомах тезис о произвольном отклонении ("клинамене") атомов от движения по прямой и обосновал на этом тезисе учение о неизбежности порождения атомами бесчисленного множества миров. Маркс подчеркивал диалектичность идеи «отклонения», изгнавшей инертность из представлений об атоме благодаря тому. что в этой идее"… осуществлено противоречие, заложенное в понятии атома" (К. Маркс и Ф. Энгельс. Соч., т. 40, с. 176).
(обратно)
Тейяр намекает на идею неисчерпаемости атома, сформулированную французским философом и естествоиспытателем Блезом Паскалем (1623–1662) в его посмертно опубликованных «Мыслях». Паскаль берет клеща как "одно из мельчайших среди ведомых людям существ", показывает сложнейшее строение его организма несмотря на крохотный размер, выделяет в этом организме все более и более мелкие части, вплоть до "капель соков", "пузырьков газа" и атомов и, наконец, предлагает: "Пусть человек представит себе неисчислимые Вселенные в этом атоме, и у каждой — свой небесный свод, и свои планеты, и своя Земля, и те же соотношения, что в зримом мире. и на этой Земле — свои животные и, наконец, свои клещи, которых опять-таки можно делить, не зная отдыха и срока, пока не закружится голова от второго чуда, столь же поразительного в своей малости, как первое — в своей огромности" (Б. Паскаль. Мысли. Пер. Э. Липецкой. В кн.: Ф. Ларошфуко. Максимы. Б. Паскаль. Мысли. Ж. Лабрюйер. Характеры. М., 1974, с. 122). Под "первым чудом" Паскаль разумеет здесь бесконечный размер Вселенной, по сравнению с которым человек и все, что он может охватить своей мыслью, есть лишь «атом».
(обратно)
Судя по обращению в этом разделе к античной натурфилософии (ср. примеч. 2), Тейяр имеет здесь в виду вихри Демокрита (460–370 гг. до н. э.), возникающие в результате отталкивания и столкновения атомов. Однако не исключено, что Тейяр вспоминает здесь и об учении о вихрях своего соотечественника Р. Декарта (1596–1650), весьма популярном (как основа механики) во Франции даже в посленьютоновское время. Вихри в представлении Декарта действительно имели силовой или энергетический характер и порождали планеты, кометы, "сферу неподвижных звезд" и едва ли не (пользуясь выражением Тейяра) "все. что в мире имеет форму".
(обратно)
О "двух безднах" Б. Паскаля, т. е. о бесконечности Вселенной и бесконечной делимости вещества, см. выше, примеч. 3.
(обратно)
Pari passu (лат.) в том же ритме, параллельно, одновременно.
(обратно)
В этом споре, развернувшемся по поводу конкурсной темы Парижской академии наук на 1858 г. ("Экспериментально осветить новыми данными вопрос о самозарождении"), Л. Пастер (1822–1895), основатель современной биохимии и иммунологии, доказал, что всегда, когда устранялась возможность проникновения бактерий, простейших и т. д. в предварительно стерилизованный растительный или животный настой, в нем не зарождалось никаких организмов. В эксперименте оппонента Пастера, врача и эмбриолога Ф.-А. Пуше, стерилизация не доводилась до конца, чем и объясняется полученный им в ряде случаев «положительный» результат, якобы указывавший на самозарождение в современных условиях. В ходе своих опытов Пастер не только опроверг этот результат, но и разработал методику количественного определения сравнительного богатства (по числу видов и особей) микрофауны различных местностей. Неоднократно делались попытки необоснованного распространения данных, полученных Пастером, на самозарождение вообще.
(обратно)
Предположение Тейяра не обоснованно. В ряде опытов, предпринятых в ходе полемики с Пуше (см. предыдущее замечание), Пастер принимал специальные меры предосторожности против «порчи» (при стерилизации) отобранных проб воздуха.
(обратно)
Имеется в виду "парадокс трансформизма", раскрытый Тейяром еще за несколько лет до того. как он начал писать "феномен человека". Начало, «черешок» каждой филы или эволюционного ствола само еще не является ее типичным компонентом и обычно сливается в восприятии палеонтолога или эволюциониста с филой-источником. либо же вообще ускользает от внимания исследователя в силу скудости сохраняющегося и дошедшего до нас материала (Р. Teilhard de Chardin. Le paradoxe transformiste. "Rev. Quest. Sci.". 1925, № 7. p. 53–80).
(обратно)
Здесь Тейяр ссылается на идею французского философа-феноменолога. математика и экономиста Ангуана Огюстена Курно (1801–1877). изложенную в его "Очерке об основах наших знаний и об особенностях философской критики" ("Essai sur les fondements de nos connaissance et sur les caracteres de la critique philosophique", Paris. 1851).
(обратно)
Имеется в виду эволюционно-палеонтологическое направление, созданное в США Генри Фейрфилдом Осборном (1857–1953), автором многих работ по филогенезу млекопитающих. Цитируемая в тексте идея высказывалась Осборном в 10–30-х годах XX в., когда он отошел от первоначально отстаивавшегося им ламаркизма и предпринял попытку синтезировать (для объяснения эволюции) виталистические и энергистские концепции с элементами неодарвинизма. Осборновская концепция «аристогенов» или "генов прогресса" послужила одним из источников учения Тейяра о радиальной энергии.
(обратно)
В своей общей схеме эволюции Тейяр во многом опирается на работы одного из первых французских генетиков Люсьена Кено (1866–1951). развивавшего концепцию преадаптации и «антислучайности» в противовес якобы основанному лишь на факторе «случайности» дарвиновскому естественному отбору. Приводимая Тейяром схема Кено была в 30–40-е годы принята практически всеми французскими эволюционистами как классическая и имеет то преимущество перед многими другими "филогенетическими деревьями", что в ней иллюстрирована множественность направлений освоения суши и воздушной среды в различных эволюционных стволах животного мира. В § 2 "Подъем сознания" главы III ("Мать-Земля") данного раздела Тейяр применяет концепцию «антислучайности» Кено для разделения двух "зон эволюции — дарвинистской. где закономерность пробивается сквозь массу случайностей, и ламаркистской. где она "ощутимо доминирует". К второй зоне Тейяр относит прежде всего эволюцию человека: практически различие между «зонами» соответствует различию между биологической и культурной эволюцией. Тейяр вслед за Кено явно недооценивает закономерного характера эволюции под действием естественного отбора.
(обратно)
Закономерность, характеризующая «дарвиновскую» эволюцию, не имеет ничего общего с "неоламаркистским антислучаем", включающим прямое приспособление, наследование приобретенных признаков и прочие умозрительные конструкты. О влиянии на Тейяра в данном вопросе взглядов Л. Кено см. предыдущее примечание.
(обратно)
См. примеч. 11.
(обратно)
Здесь Тейяр подошел к идее генезиса сознания на базе раннесоциальных структур, но потерпел неудачу в силу недостатков своей методологии. Он признает, что появление сознания каким-то образом есть результат возрастания материальной сложности. но в то же время отмечает ("парадокс человека"), что анатомическое отличие человека от других антропоидов несравненно слабее, чем его "умственное превосходство". Допуская межиидивидуальное происхождение мысли, Тейяр не может сделать решающего шага к разъяснению этой межиндивидуальности, поскольку у него отсутствует трудовая теория антропогенеза. В результате он вынужден отказаться от анализа "более глубоких причин, направляющих всю игру", и скрыться под "феноменалистическим покрывалом": ему представляется достаточным позволить читателю поместить под факты генезиса сознания из интеракции любое онтологическое строение мира. "которое ему заблагорассудится". то есть как материалистическое, так и идеалистическое (ср. примеч. 1).
(обратно)
Термин «гермен» для обозначения «зародышевого» (франц. germe зародыш) или наследственного вещества заимствован Тейяром у Л. Кено (см. примеч. 12).
(обратно)
Имеется в виду вышедший в 1883–1909 гг. трехтомный труд австрийского геолога Эдуарда-Фридриха Зюсса (1831–1914) "Лик Земли", где подробно разработано понятие биосферы как особой оболочки Земли (наряду с литосферой, гидросферой, атмосферой). Ранее это понятие было теоретически обосновано Зюссом в его работах конца XIX века, впервые же оно встречается (под другими терминами) еще в работах Ж.-Б. Ламарка.
(обратно)
Уильям Кинг Грегори (1876–1952), американский палеонтолог, работал в Нью-Йоркском музее естественной истории, в 1907–1943 гг. профессор палеонтологии Колумбийского университета (Нью-Йорк). Основные работы: по эоценовым приматам; по морфологии и эволюции черепа и локомоторной системы млекопитающих и других позвоночных; по филогении рыб.
(обратно)
Гейдельбергский человек. Homo heidelbergensis, вид ископаемого человека, установленный на основании единственной нижней челюсти, которая была в 1907 г. найдена немецким антропологом О. Шётензаком на глубине 24 м в долине р. Эльсенц у деревни Мауэр близ Гейдельберга (ныне ФРГ, земля Баден-Вюртемберг). Позже в той же местности был найден ряд кремневых обломков, носящих следы искусственной обработки. Ее характер и строение челюсти позволяют ориентировочно сближать гейдельбергского человека (жившего 400 тыс. лет назад, т. е. в раннем плейстоцене) с питекантропом и синантропом.
(обратно)
Марселлен-Пьер Буль (1861–1942), французский геолог и антрополог. профессор геологии в университете города Клермон-Феррана, а затем (1902–1936) в парижском Национальном музее естественной истории, где под его руководством в двадцатые годы работал Тейяр. Первым (в 1908 г.) реконструировал полностью скелет неандертальца. После открытия синантропа выдвинул не подтвердившуюся впоследствии и критикуемую Тейяром гипотезу о том, что орудия, остатки костров и прочие следы жизнедеятельности синантропа в действительности принадлежат не ему, а другому виду людей, возможно, стоявшему на уровне развития, более близком к неандертальцам.
(обратно)
Ключевой момент антропогенеза, восходящий к раннему палеолиту, освещен Тейяром бегло и явно недостаточно. Этот момент или, точнее, этап характеризовался качественным переходом от биологической эволюции к формам социально-культурного прогресса как явления, отсутствовавшего на всех более ранних этапах. На этом переходном этапе факторы социально-культурного порядка и прежде всего труд выступают также и как факторы антропогенеза, включающего и биологическое (например, анатомическое, функциональное и т. д.) совершенствование человеческого организма. Именно на этом этапе рука, строение которой явилось первичным стимулом для выделения человека из животного мира, уже является, как пишет Ф. Энгельс, "не только органом труда, она также и продукт его" (К. Маркс и Ф. Энгельс. Соч., т. 20, с. 488). Начиная с этого этапа, человек становится существом, имеющим собственно человеческую и общественную (а не просто биологическую, видовую, природную) историю: "Первый исторический акт этих индивидов, благодаря которому они отличаются от животных, состоит не в том, что они мыслят, а в том, что они начинают производить необходимые им средства к жизни" (К. Маркс и Ф. Энгельс. Соч., т. 3, с. 19). Преимущественно в связи с этим этапом встает и вопрос о формировании речи, которого Тейяр не затрагивает. Между тем только для существа, обладающего членораздельной речью, то есть для человека, становится возможным развитие понятийного аппарата мышления и создается ситуация (раскрытая, например, в трудах С. Л. Рубинштейна), когда в каждом единичном факте или наборе обстоятельств содержится смысловое значение, а предметы приобретают независимость от контекста, в котором они непосредственно даны.
(обратно)
Анри-Эдуард-Проспер Брей (1877–1961), французский археолог, один из пионеров исследования палеолитического искусства. Автор многих монографий по пещерным и скальным изображениям Франции, Испании, Южной и Юго-Западной Африки. В 1912 г. описал ориньякскую культуру, существовавшую около 20–35 тысяч лет назад и признаваемую в настоящее время одним из важнейших этапов позднего европейского палеолита. Был ближайшим другом Тейяра с двадцатых годов и до его смерти, а затем одним из инициаторов посмертного издания собрания сочинений Тейяра.
(обратно)
Имеются в виду геологические работы французского естествоиспытателя Жоржа-Луи-Леклерка Бюффона (1707–1788), в том числе его "Теория Земли" (1749 г.), геологические разделы "Естественной истории" (тт. 1–36, 1749–1788 гг.) и в особенности "Эпохи природы" (1778 г.). В последней из перечисленных работ дана попытка разделения истории Земли на периоды (на семь эпох), а общий возраст Земли определен в 75 тысяч лет, что для того времени было почти фантастически смелым.
(обратно)
ipso facto — тем самым (лат.).
(обратно)
Б. Паскаль в своих «Мыслях» доказывает невозможность рациональными доводами подтвердить или опровергнуть бытие бога и далее предлагает решить этот вопрос с помощью бросания монеты. "Давайте взвесим ваш возможный выигрыш или проигрыш, если вы поставите на орла, то есть на бога. Выиграв, вы обретаете все, проиграв, не потеряете ничего… Таким образом, если не играть нельзя, лучше отказаться от разума во имя жизни, лучше рискнуть им во имя бесконечно большого выигрыша, столь же возможного, сколь возможно и небытие" (Б. Паскаль. Мысли. — В кн.: Ф. Ларошфуко. Максимы. Б. Паскаль. Мысли. Ж. Лабрюйер. Характеры. М., 1974, с. 155).
(обратно)
Леон Брюнсвик (1869–1944), французский философ, представитель школы "критического рационализма". Тейяр имеет в виду его работы "Введение в жизнь духа" (1900 г.) и "Прогресс сознания в западной философии" (1927 г.), где утверждается тезис о том, что научное знание и мораль образуют некоторое единство высшего порядка, венчающее собой мировой эволюционный процесс.
(обратно)
"Eppur si muove!" (итал.) "А все-таки она вертится!". Слова, приписываемые легендой Галилею и якобы сказанные им, когда он выходил из судилища инквизиции после своего вынужденного отречения от принципа вращения Земли вокруг Солнца (21 июня 1633 г.).
(обратно)
Имеется в виду прежде всего диалог Платона «Пир»: "любовью называется жажда целостности и стремление к ней" (Платон, Сочинения в трех томах. Т. 2. М., 1970, с. 120). Один из участников диалога, врач Эриксимах (историческое лицо), говорит, что бог любви Эрот разлит по всей природе: "… живет он не только в человеческой душе и не только в ее стремлении к прекрасным людям, но и во многих других ее порывах, да и вообще во многом другом на свете — в телах любых животных, в растениях, во всем, можно сказать, сущем, ибо он бог великий, удивительный и всеобъемлющий, причастный ко всем делам людей и богов" (Там же, стр. 112).
(обратно)
Николай Кузанский (1401–1464), философ раннего Возрождения, излагает свою теорию связующей роли любви, например в трактате "Охота за мудростью": "… любовь, связь единства и бытия, в высшей степени природна. Она исходит от единства и равенства, в которых ее природное начало: они дышат своей связью, и в ней неудержимо жаждут соединиться. Ничто не лишено этой любви, без которой не было бы ничего устойчивого; все пронизано невидимым духом связи, все части мира внутренне хранимы ее духом, и каждая соединяется им с миром. Этот дух связывает душу с телом, и она перестает животворить тело, когда он отлетает. Интеллектуальная природа никогда не может лишиться духа связи, поскольку сама соприродна этому духу; единство и бытие интеллектуальной природы интеллектуальны и потому скрепляются интеллектуальной связью, и эта связь, интеллектуальная любовь, не может ни кончиться, ни ослабнуть, пока жизнь интеллекта, понимание, питается бессмертной премудростью. Природная связь в интеллектуальной природе, тяготеющей к премудрости, не только сохраняет поэтому интеллектуальную природу в ее существовании, но и приближает ее к тому, что она по своей природе любит, вплоть до соединения с ним". (Николай Кузанский. Сочинения в двух томах. Т. 2. М., 1980, с. 386–387).
(обратно)
Уильям Диллер Мэттью (1871–1930), американский палеонтолог. Основные работы по ископаемым позвоночным Нового Света. Работал в Музее естественной истории в Нью-Йорке; с 1927 г. профессор палеонтологии в Калифорнийском университете. Мысль, приводимая Тейяром, развита Мэттью в работах "Климат и эволюция" (1915 г.) и "Эволюция млекопитающих в эоцене" (1927 г.).
(обратно)
Алексис Каррель (1873–1944), французский биолог и хирург-экспериментатор. Лауреат Нобелевской премии по медицине за 1912 г. (за разработку новых методов лечения и заживления ран). С 1904 года работал в США (в Физиологическом институте в Чикаго и затем в Рокфеллеровском центре в Нью-Йорке). Приведенная Тейяром фраза представляет собой заглавие научно-популярного труда Карреля, изданного в 1935 г.
(обратно)
В этой гипотезе Тейяр выступает в явное противоречие с оптимистическими предсказаниями, данными выше в разделе "Организация научных исследований". Таким образом, задача, поставленная им в начале главы "Коллективный выход" (см. "Предварительное замечание: тупик, который необходимо избежать") оказывается невыполненной, а тупик индивидуализма и разрозненности людей — непреодоленным иначе, как в "кончине Земли". Столь же не случайно и отсутствие у Тейяра хотя бы намека на конкретные пути преодоления этого тупика. Это абстрактное, в конечном счете экстраполирующее биологический прогресс и регресс на всю социальную сферу, понимание настоящего и будущего общества отражает радикальное отличие и обедненность утопий и антиутопий Тейяра по сравнению с социалистическими учениями (не только с марксизмом, но и с утопическим социализмом). Отсюда естественна и неудача попыток сблизить тейяровскую трактовку человека с социалистическим гуманизмом в духе Ж. Жореса (см., например, такое малообоснованное сопоставление в работе ближайшего ученика Тейяра, П. Шошара: Р. Chauchard. Teilhard de Chardin, l'humanisme socialiste et la reconcilation des humanismes. «Synthese», 1960, № 169–170. В своей, несомненно, гуманистичной по интенции схеме Тейяр рисует движение человечества от преодоления индивидуализма (через общение, основанное на росте технических средств коммуникации) к "осознанию самого себя"; но эта схема остается благим пожеланием, никак не поддержанным и не обеспеченным со стороны механизма этого процесса или в плане выяснения реальных социально-ценностных основ общения и самосознания. Наиболее значимыми и рельефными в этой схеме остаются моменты, наиболее основанные на опыте Тейяра как ученого и связанные с его пониманием глобальной важности организации науки и ее потенциальной роли, как "не побочного занятия, а существенной формы деятельности".
(обратно)
ААА
Ауыспа таңбалы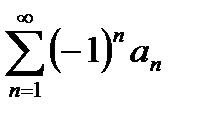 
қатарының жинақты болу шартын көрсетіңіз
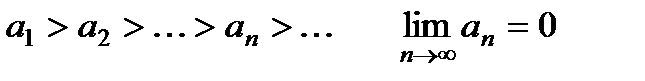
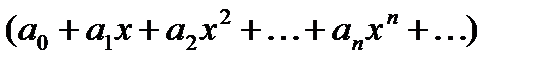дәрежелік қатардың жинақтылық радиусын көрсетіңіз
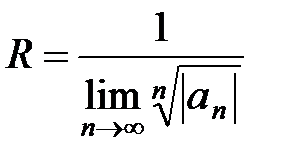
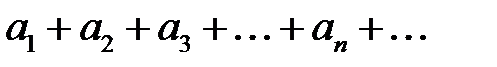қатарының абсолютті жинақты болу шартын көрсетіңіз
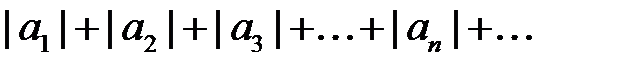қатар жинақты
нені білдіреді?
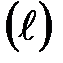қисығы бойымен материалдық нүктені 
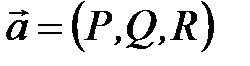- күш векторы әсерімен жылжыту кезіндегі жасалатын жұмыстың мөлшері
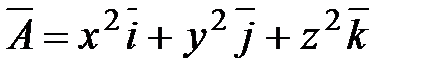векторлық өрістің дивергенциясын табыңыз
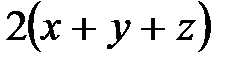
Мына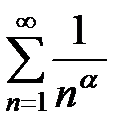 
, ( 
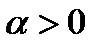) сандық қатары үшін дұрыс тұжырымды көрсетіңіз
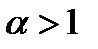болса қатар жинақты
БББ
Бағдарланған қисықтар анықтамасы:
Бастапқы және соңғы нүктелері мен қозғалыс бағыты көрсетілген қисықтарды айтады
Бағдарланған беттер анықтамасы:
Әрбір нүктесіндегі бетке тұрғызылған нормаль вектор мен контур бойымен айналу бағыты көрсетілген беттерді айтады
ГГГ
Грин формуласының көмегімен тқйық сызықтың ауданын есептеу формуласы:
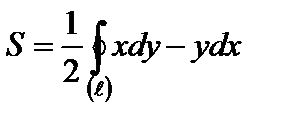
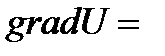
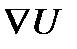
Гармоникалық қатарды көрсетіңіз
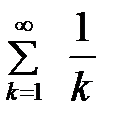
ДДД
Даламбер белгісі бойынша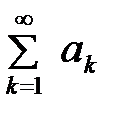 
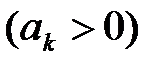қатары жинақты, егер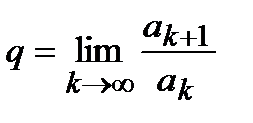 
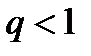
Дәрежелік қатардың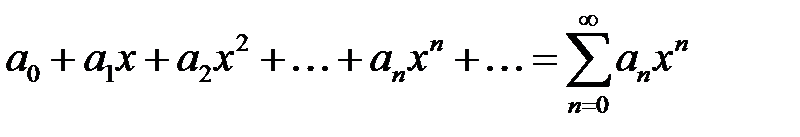 
жинақтылық радиусын көрсетіңіз
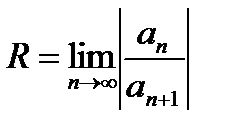
Дәрежелік қатардың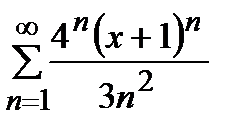 
жалпы мүшесінің коэффициенті тең:
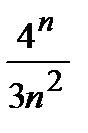
Дәрежелік қатардың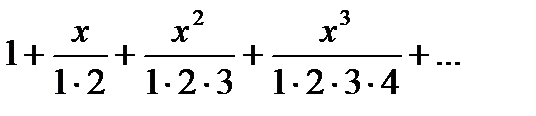 
жалпы мүшесі келесі функция болады:
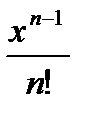
Дәрежелік қатардың 
жалпы мүшесі келесі өрнек болады:
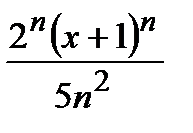
Дәрежелік қатардың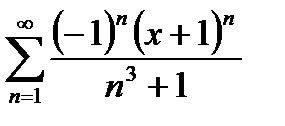 
жалпы мүшесінің коэффициенті тең:
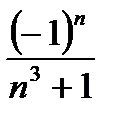
Дәрежелік қатардың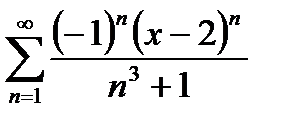 
жалпы мүшесі келесі өрнек болады:
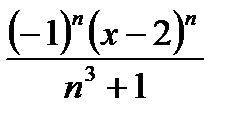
Дәрежелік қатардың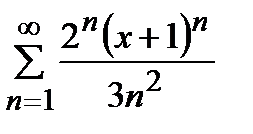 
жалпы мүшесі келесі өрнек болады:
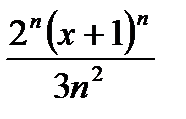
Дәрежелік қатардың 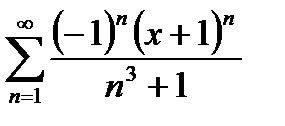жалпы мүшесінің коэффициенті тең:
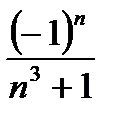
Орта мән туралы теорема
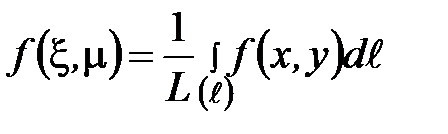
ФФФ
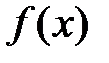функциясының 
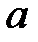нүктесінде Тейлор қатарына жіктелуін көрсетіңіз
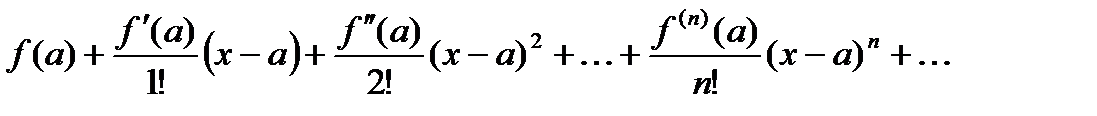
Функциялық қатарды көрсетіңіз
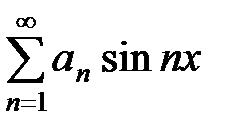
Функционалдың анықтамасы:
Нақты мәндік функциялардың анықталу облысы кез-келген объектілер жиыны болғанда, оларды функционалдар деп атайды.
Функционалды есептеңіз
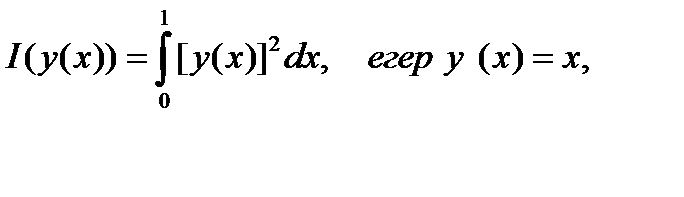EEE
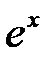функциясының Маклорен қатарына жіктелуін көрсетіңіз
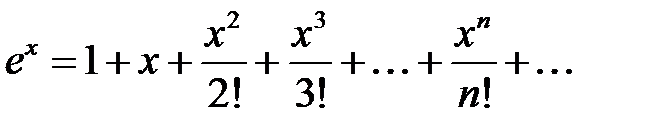
Егер сандық қатар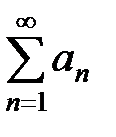 
жинақты болса, онда
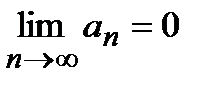
Егер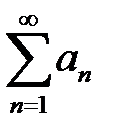 
және 
қатарларының 
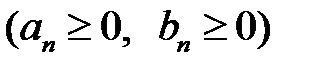мүшелері үшін 
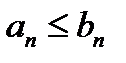теңсіздіктер орындалса, онда
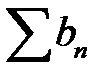қатарының жинақтылығынан 
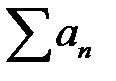қатардың жинақтылығы шығады
Егер 
болса, онда 
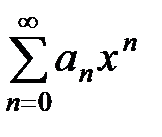дәрежелік қатарының жинақтылық радиусы неге тең?
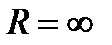
Егер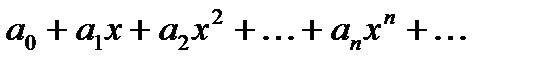 
дәрежелік қатары нөлге тең емес 
нүктесінде жинақты болса, онда
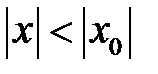теңсіздігін қанағаттандыратын барлық 
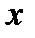-тер үшін қатар абсолютті жинақты болады
Егер дәрежелік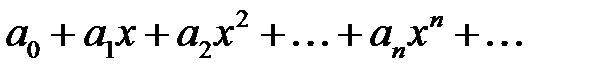 
- қатары 
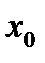нүктесінде жинақсыз болса, онда ол
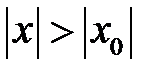теңсіздігін қанағаттандыратын барлық 
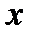-тер үшін жинақсыз болады
Егер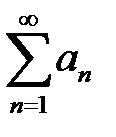 
қатары жинақты болса, онда 
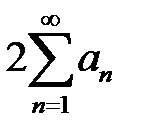қатары туралы не айтуға болады?
жинақты
Егер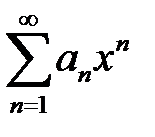 
қатары 
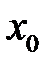нүктесінде жинақты болса, онда қатар
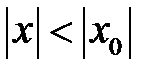болғанда әрбір 
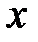нүктесінде абсолютті жинақты
Егер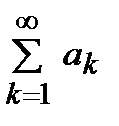 
, 
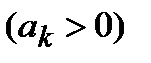жинақты, ал 
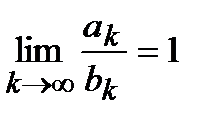болса, онда 
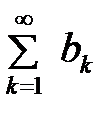қатары
жинақты
-ге дейінгі дәлдікпен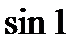 
шамасын есептеу өрнегін көрсетіңіз
A)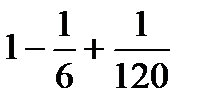 
Есепте: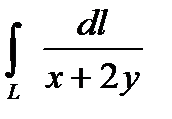 
, мұндағы 
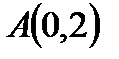мен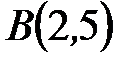 
аралығындағы 
түзу
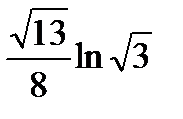
Есепте: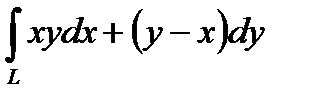 
, мұндағы 
мен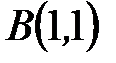 
аралығындағы 
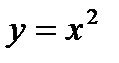параболаның доғасы
1/12
Егер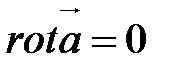 
, онда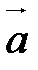 
потенциалды өріс
1/3
ҚҚҚ
Қатар жинақтылығының Коши белгісін көрсетіңіз
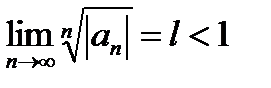
Қатар жинақтылығының Даламбер белгісін көрсетіңіз
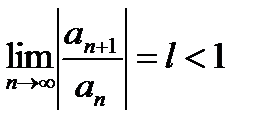
Қатар жинақты деп аталады, егер
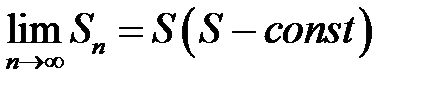
Қисық сызық бойымен алынған бірінші текті қисық сызықты интегралы көрсетіңіз
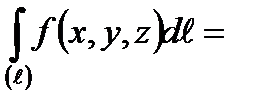
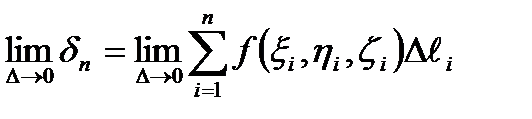
(синус,косинус)
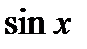функциясының Маклорен қатарына жіктелуін көрсетіңіз
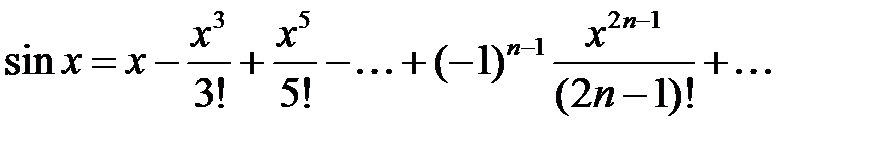
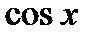функциясының Маклорен қатарына жіктелуін көрсетіңіз
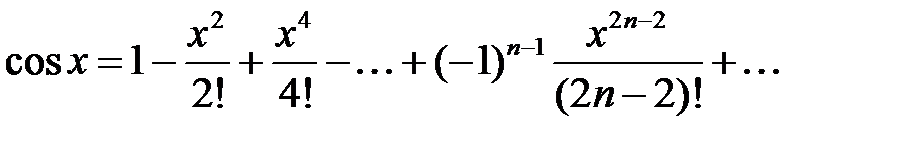
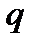параметрінің қандай мәндерінде 
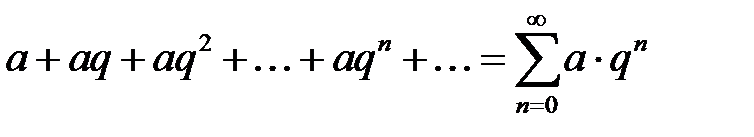қатары жинақты?
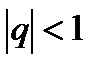
p – параметрінің қандай мәндерінде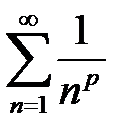 
- Дирихле қатары жинақты болады?
Уууууу
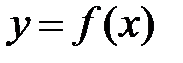функциясы үшін Маклорен қатарының жалпы мүшесі
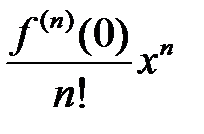
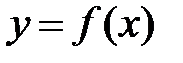функциясы үшін 
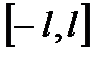кесіндісіндегі Фурье қатарының коэффициенттері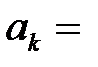 
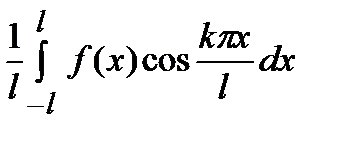
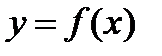функциясы үшін 
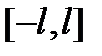кесіндісіндегі Фурье қатарының коэффициенттері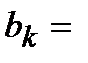 
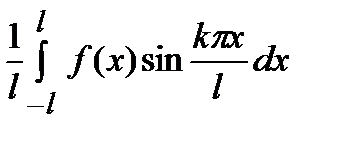
π π π π
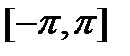кесіндісіндегі 
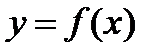жұп функциясы үшін Фурье қатары-
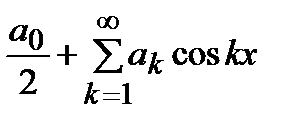
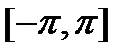кесіндісіндегі 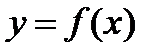тақ функциясы үшін Фурье қатары-
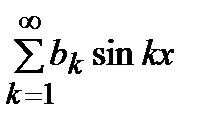
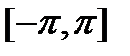кесіндісіндегі 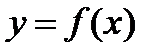жұп функциясы үшін Фурье қатарының коэффициенттері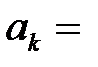
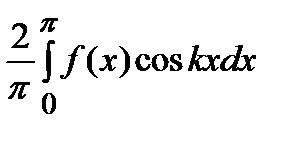
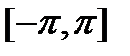кесіндісіндегі 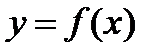тақ функциясы үшін Фурье қатарының коэффициенттері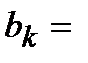
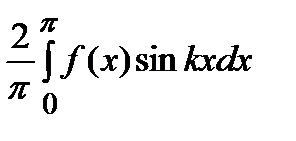
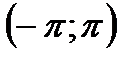интервалында берілген 
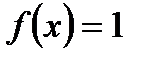функциясын Фурье қатарына жіктеңіз
A) 1
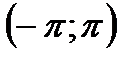интервалында берілген 
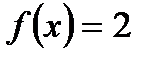функциясын Фурье қатарына жіктеңіз
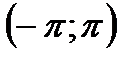интервалында берілген 
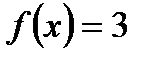функциясын Фурье қатарына жіктеңіз
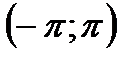интервалында берілген 
функциясын Фурье қатарына жіктеңіз
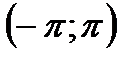интервалында берілген 
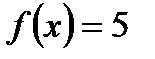функциясын Фурье қатарына жіктеңіз
εεεεεε
-ге дейінгі дәлдікпен 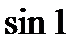шамасын есептеу өрнегін көрсетіңіз
A)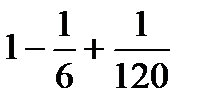
Сумма
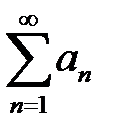- қатарының жинақты болуының қажетті шартын көрсетіңіз
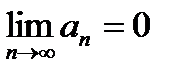
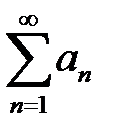қатарының жинақсыз болуының жеткілікті шартын көрсетіңіз
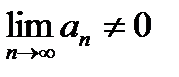
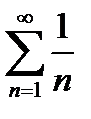гармоникалық қатары қандай болады?
жинақсыз
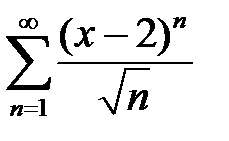қатарының жинақтылық облысын табыңыз
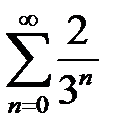қатарының қосындысын табыңыз
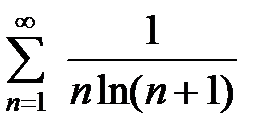қатарды жинақтылыққа зерттеңіз
жинақсыз
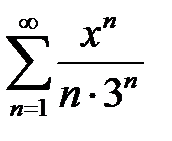қатардың жинақтылық облысын табыңыз
[-3, 3)
қатардың жинақтылық облысын табыңыз
(-1,5)
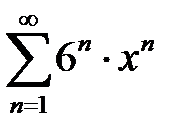қатардың жинақтылық радиусын табыңыз
1/6
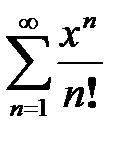қатардың жинақтылық радиусын табыңыз
+ 
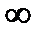
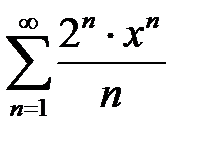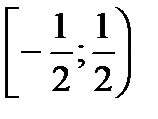
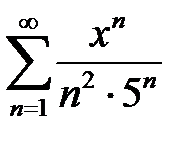қатардың жинақтылық облысын табыңыз
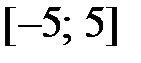
қатардың жинақтылық облысын табыңыз
қатардың жинақтылық облысын табыңыз
(4,5; 5,5)
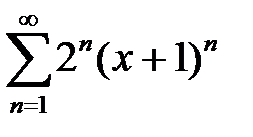қатардың жинақтылық облысын табыңыз
(-1,5; -0,5)
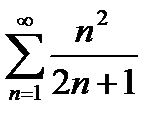қатарын жинақтылыққа зерттеңіз
жинақсыз
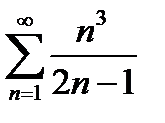қатарын жинақтылыққа зерттеңіз
жинақсыз
$$$ 40
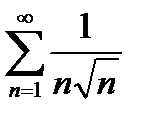қатарының жинақтылыққа зерттеңіз
жинақты
$$$ 41
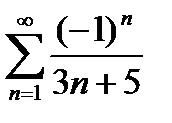қатардың төртiншi мүшесiн табыңыз
1/17
$$$ 42
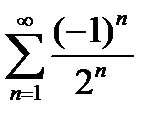қатардың төртiншi мүшесiн табыңыз
1/16
$$$ 43
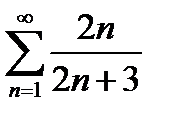қатардың бесінші мүшесiн табыңыз
10/13
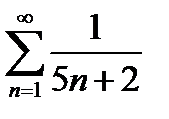қатарының алғашқы екі мүшесінің қосындысын табыңыз
19/84
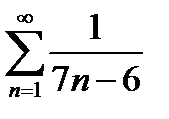қатарының алғашқы екі мүшесінің қосындысын табыңыз
9/8
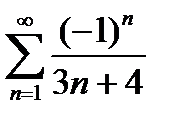қатарының алғашқы екі мүшесінің қосындысын табыңыз
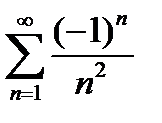қатарының алғашқы екі мүшесінің қосындысын табыңыз
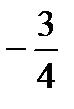
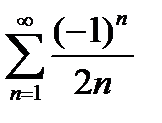қатарының үшінші және бесінші мүшелерінің қосындысын табыңыз
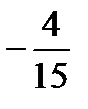
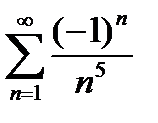қатарды жинақтылыққа зерттеңіз
абсолютті жинақты
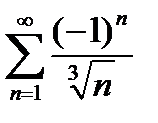қатарды жинақтылыққа зерттеңіз
шартты жинақты
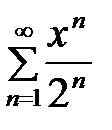қатардың жинақтылық радиусын табыңыз
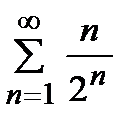қатарын жинақтылыққа зерттеніз
жинақты
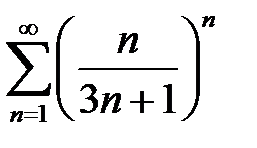қатарды жинақтылыққа зерттеңіз
жинақты
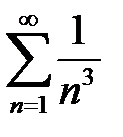қатарды жинақтылыққа зерттеңіз
жинақты
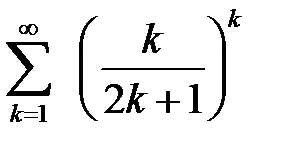қатарын жинақтылыққа зерттеңіз
жинақты
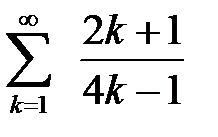қатарын жинақтылыққа зерттеңіз
жинақсыз
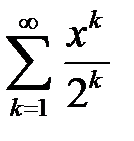қатарының жинақтылық аралығын табыңыз
(–2,2)
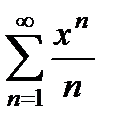қатарының жинақтылық радиусын табыңыз
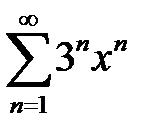қатарының жинақтылық радиусын табыңыз
1/3
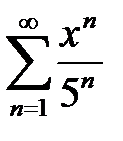қатарының жинақтылық радиусын табыңыз
қатарының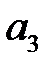 
және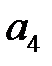 
мүшелерінің қосындысын табыңыз
2/15
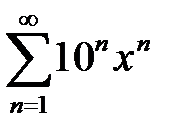қатарының жинақталу интервалын табыңыз
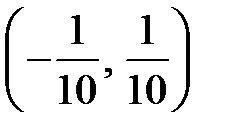
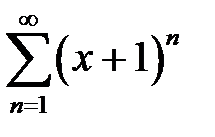қатарының жинақтылық интервалын табыңыз
(-2; 0)
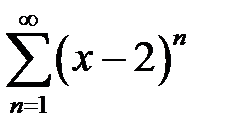қатарының жинақтылық интервалын табыңыз
(1; 3)
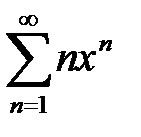қатарының жинақтылық интервалын табыңыз
(-1; 1)
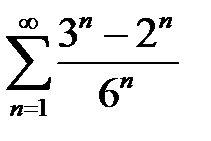қатарының қосындысын табыңыз
0,5
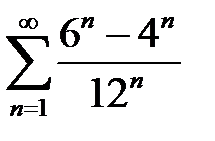қатарының қосындысын табыңыз
0,5
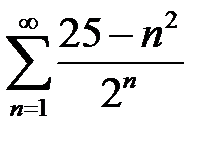қатарының бірінші және үшінші мүшелерінің айырымын табыңыз
қатарының бірінші және үшінші мүшелерінің қосындысын табыңыз
17,25
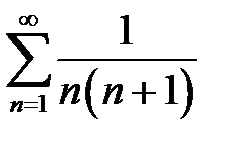қатарының қосындысын табыңыз
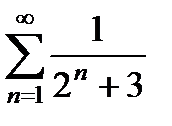қатарының алғашқы екі мүшесінің қосындысын табыңыз
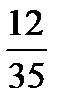
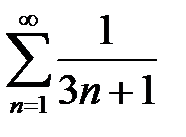қатарының алғашқы үш мүшесінің қосындысын табыңыз
69/140
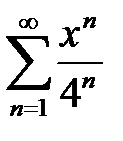дәрежелік қатардың жинақтылық радиусын табыңыз
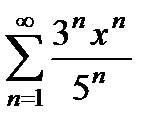дәрежелік қатардың жинақтылық радиусын табыңыз
5/3
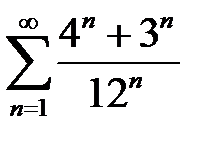қатарының қосындысын табыңыз
5/6
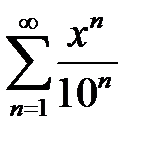дәрежелік қатардың жинақталу радиусын табыңыз
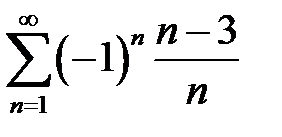қатарының екінші және төртінші мүшелерінің қосындысын табыңыз
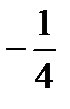
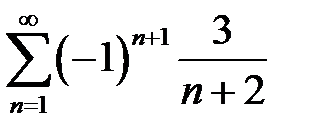қатарының екінші және үшінші мүшелерінің қосындысын табыңыз
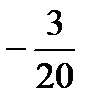
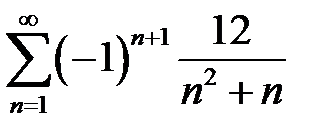қатарының екінші және үшінші мүшелерінің қосындысын табыңыз
-1
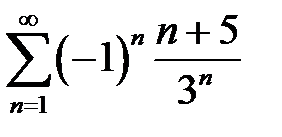қатарының екінші және үшінші мүшелерінің қосындысын табыңыз
13/27
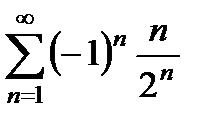қатарының алғашқы үш мүшесі мынадай:
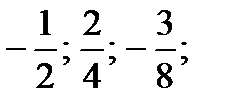
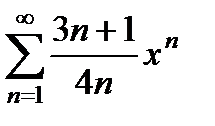қатарының жинақтылық радиусы тең
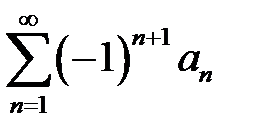ауыспалы таңбалы қатары жинақты және оның қосындысы 
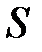- ке тең болса, онда
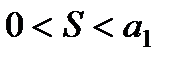
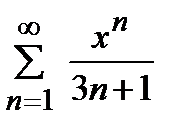дәрежелік қатарының жинақтылық радиусы тең:
1.
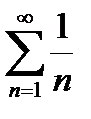қатары қандай қатар деп аталады:
Гармоникалық. .
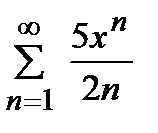дәрежелік қатарының жинақтылық радиусы тең:
1.
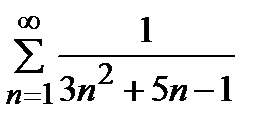қатарын жинақтылыққа зерттеңіз
жинақты
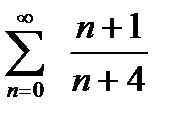қатарының жинақтылығын зерттеу үшін жинақтылықтың мынадай белгісін қолданамыз:
Жинақтылықтың қажеттілік белгісі
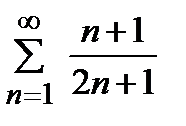қатарын жинақтылыққа зерттеңіз
жинақсыз
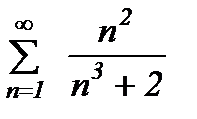қатарын жинақтылыққа зерттеңіз
жинақсыз
қатарын жинақтылыққа зерттеңіз
жинақсыз
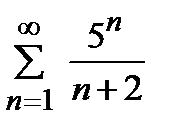қатарын жинақтылыққа зерттеңіз
жинақсыз
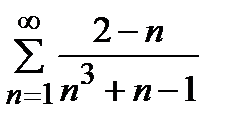қатарын жинақтылыққа зерттеңіз
жинақты
қатарын жинақтылыққа зерттеңіз
жинақсыз
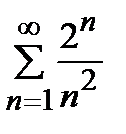қатарын жинақтылыққа зерттеңіз
жинақсыз
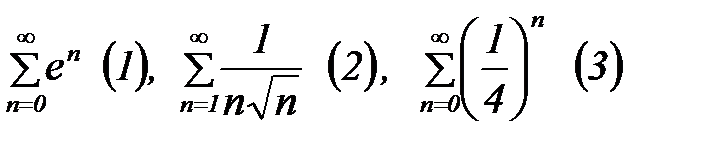қатарларының қайсысы жинақсыз қатар болады?
1.
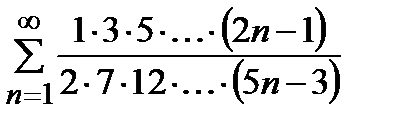қатарын жинақтылыққа зерттеңіз
жинақты
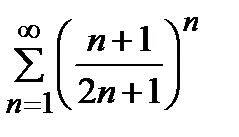қатарын жинақтылыққа зерттеңіз
жинақты
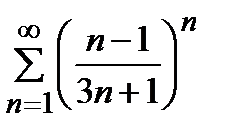қатарын жинақтылыққа зерттеңіз
жинақты
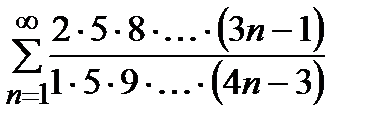қатарын жинақтылыққа зерттеңіз
жинақты
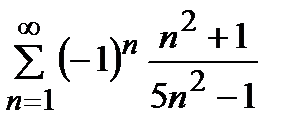қатарын жинақтылыққа зерттеңіз
жинақсыз
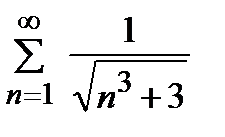қатарын жинақтылыққа зерттеңіз
жинақты
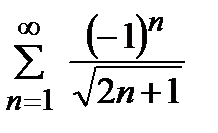қатарын жинақтылыққа зерттеңіз
шартты жинақты
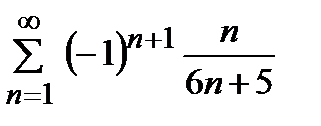қатарын жинақтылыққа зерттеңіз
жинақсыз
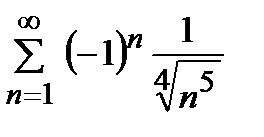қатарын жинақтылыққа зерттеңіз
абсолютті жинақты
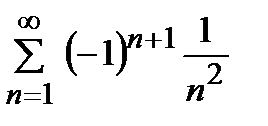қатарын жинақтылыққа зерттеңіз
абсолютті жинақты
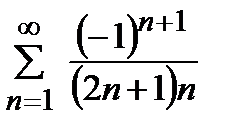қатарын жинақтылыққа зерттеңіз
абсолютті жинақты
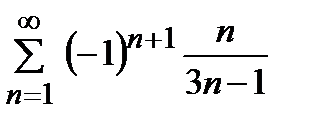қатарын жинақтылыққа зерттеңіз
жинақсыз
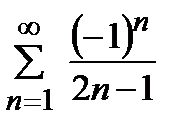қатарын жинақтылыққа зерттеңіз
шартты жинақты
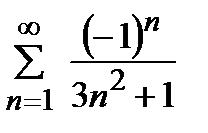қатарын жинақтылыққа зерттеңіз
абсолютті жинақты
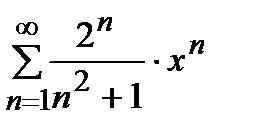дәрежелік қатарының жинақтылық радиусы тең:
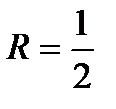
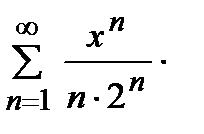дәрежелік қатарының жинақтылық радиусы тең:
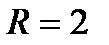
$$$ 141
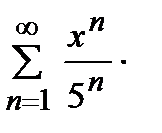дәрежелік қатарының жинақтылық радиусы тең:
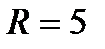
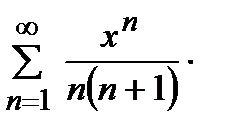қатарының жинақталу облысын табыңыз
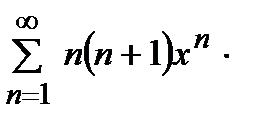қатарының жинақталу облысын табыңыз
(-1, 1)
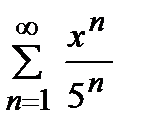қатарының жинақталу облысын табыңыз
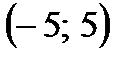
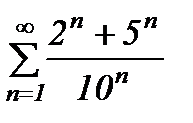қатарының қосындысын табыңыз
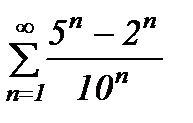қатарының қосындысын табыңыз
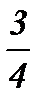
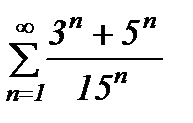қатарының қосындысын табыңыз
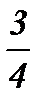
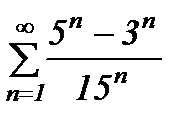қатарының қосындысын табыңыз
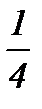
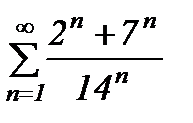қатарының қосындысын табыңыз
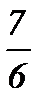
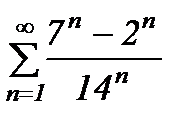қатарының қосындысын табыңыз
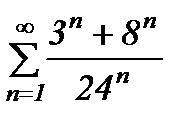қатарының қосындысын табыңыз
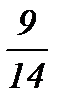
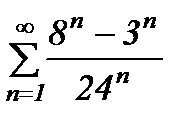қатарының қосындысын табыңыз
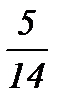
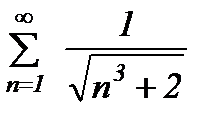қатарын жинақтылыққа зерттеңіз
жинақты
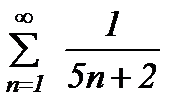қатарын жинақтылыққа зерттеңіз
жинақсыз
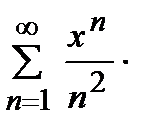қатарының жинақталу облысын табыңыз
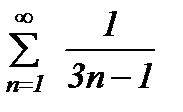қатарын жинақтылыққа зерттеңіз
жинақсыз
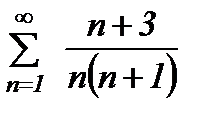қатарын жинақтылыққа зерттеңіз
жинақсыз