Функциональные зависимости надежности

Отказы, возникающие в процессе испытаний или эксплуатации, могут быть вызваны неблагоприятным сочетанием различных факторов — рассеянием действующих нагрузок, отклонением от номинального значения механических характеристик материалов, неблагоприятным сочетанием допусков в местах сопряжения и т. п. Поэтому в расчетах надежности различные параметры рассматривают как случайные величины, которые могут принимать то или иное значение, неизвестное заранее.

Различают случайные величины прерывного (дискретного) и не-прерывного типов. Условимся случайные величины в дальнейшем обозначать большими буквами, а их возможные значения — соответствующими малыми. Для каждого числа х в диапазоне изменения случайной величины Х существует определенная вероятность Р(Х<х) того, что Х не превышает значения х. Вероятность этого события называют функцией распределения:

F(х) = Р(Х<х). (3.1)

Функция распределения — универсальная характеристика, так как она является функцией как непрерывных, так и дискретных случайных величин. Функция (х) относится к неубывающим функциям — х монотонно возрастает при непрерывных процессах и ступенчато возрастает при дискретных процессах. В пределах изменения случай­ной величины X эта функция изменяется от 0 до 1: F(-∞) = 0; F(∞) = 1.

Производную от функции распределения по текущей переменной называют плотностью распределения

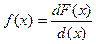(3.2)

которая характеризует частоту повторений данного значения случайной величины. В теории надежности величину f(x) называют плотностью вероятности. Плотность рас­пределения есть неотрицательная функция своего аргумента f(x) ≥ 0.

Интеграл в бесконечных пределах от плотности распределения равен единице:

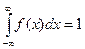
В ряде случаев в качестве характеристик распределения случайных величин достаточно использовать некоторые числовые величины, среди которых в теории надежности наиболее употребительными являются математическое ожидание (среднее значение), мода и медиана (характеризуют положение центров группирования случайных величин на числовой оси), дисперсия, среднее квадратическое отклонение и коэффициент вариации (характеризуют рассеяние случайной величины). Значения характе­ристик, полученные по результатам испытаний или эксплуатации, называют статистическими оценками. Характеристики распределения используют для прогнозирования надежности.

Для дискретных случайных величин математическое ожидание М_х равно сумме произведений всех возможных значений Х на вероятности этих значений:

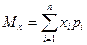
Математическое ожидание для непрерывной случайной величины выражается интегралом в бесконечных пределах от произведения непрерывно изменяющихся возможных значений случайной величины на плотность распределения

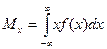
Математическое ожидание случайной величины непосредственно связано с ее средним значением. При неограниченном увеличении числа опытов среднее арифметическое значение величины х приближается к математическому ожиданию и называется оценкой среднего значения

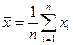
где n- общее число опытов; x_i- текущее значение случайной величины.

Дисперсией (D) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.

Для дискретной случайной величины дисперсия равна:

Для непрерывной случайной величины дисперсия определяется из выражения
Оценка дисперсии случайной величины:

Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для наглядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение о_х> которое определяется как корень квадратный из дисперсии:

Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:

Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна.

Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.

Квантиль — значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой.

Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т.е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.

Пример 3.1. Функция распределения непрерывной случайной величины X задана выражением

Найти коэффициент а и плотность распределения j(x).

Решение. Так как функция распределения случайной величины X непрерывна, то при х= 1, ах? = 1, откуда а = 1.

Механическая энергия в системе может возникнуть и как следствие тех затрат энергии, которые имели место при изготовлении отдельных частей системы и сохрани-лись в них в потенциальной форме. Например, деформация частей при перераспределе-нии внутренних напряжений, изменение объема детали после ее термической обработ-ки происходят без всяких внешних воздействий.

Тепловая энергия действует на систему и ее части при колебаниях температуры окружающей среды, при осуществлении рабочего процесса (особенно сильные тепло-вые воздействия имеют место при работе двигателей и ряда технологических машин), при работе приводных механизмов, электротехнических и гидравлических устройств.

Химическая энергия также оказывает влияние на работу системы. Даже воздух, который содержит влагу и агрессивные составляющие, может вызвать коррозию от-дельных узлов системы.

Если же оборудование системы работает в условиях агрессивных сред (обо-рудование химической промышленности, суда, многие машины текстильной промыш-ленности и др.), то химические воздействия вызывают процессы, приводящие к разру-шению отдельных элементов и узлов системы.

Ядерная (атомная) энергия, выделяющаяся в процессе превращения атомных ядер, может воздействовать на материалы (особенно в космосе), изменяя их свойства.

Электромагнитная энергия в виде радиоволн (электромагнитных колебаний) пронизывает все пространство вокруг объекта и может оказать влияние на работу элек-тронной аппаратуры.

Биологические факторы также могут влиять на работоспособность системы. Например, в тропических странах имеются микроорганизмы, которые не только разру-шают некоторые виды пластмасс, но даже могут воздействовать на металл.

Таким образом, все виды энергии действуют на техническую систему и ее меха-низмы, вызывают в ней целый ряд нежелательных процессов, создают условия для ухудшения ее технических характеристик.