Метрологические характеристики СИ

К нормируемым метрологическим характеристикам СИ в соответствии с ГОСТ 8.009-84 относятся [4]:

1. Характеристики СИ, предназначенные для определения результатов измерений:

а) функция преобразования или номинальная статическая характеристика (НСХ) Y=f(X), где Y – показания прибора или выходной сигнал преобразователя, Х – измеряемая физическая величина;

б) значение Ун однозначной или многозначной меры (например, объём мерного сосуда, эдс нормального элемента, сопротивление образцового резистора и т.д.);

в) цена деления шкалы;

г) вид выходного кода, разрядность, цена наименьшего разряда для цифровых СИ.

2. Характеристики погрешностей СИ (точностные характеристики).

3. Характеристики чувствительности СИ к влияющим величинам. Определяют особенности эксплуатации данного СИ.

4. Динамические характеристики, определяющие инерционность ИП или преобразователеля.

Класс точности является обобщённой точностной характеристикой СИ и может быть представлен следующими критериями:

1) пределом допускаемой абсолютной погрешности Δ д;

а) Δ д = ± а ;

б) Δ д = = ± ( а + в ּХ), где Х – значение измеряемой величины; а и в – постоянные величины;

2) пределом допускаемой приведённой погрешности (%)

γ = Δ дּ 100/ Хн, где Хн – нормирующее значение.

Оно может определяться как

- максимальное значение шкалы прибора, если её минимальное значение равно нулю;

- разница конечных значений шкалы прибора, если нулевая отметка отсутствует;

- сумма конечных значений шкалы, если нулевая отметка находится внутри шкалы;

- номинальное значение измеряемой величины, если таковое установлено.

3) пределом допускаемой относительной погрешности δ д:

а) δ д =Δ д · 100/Х ;

б) δ д = ± [с + d· (Xmax /X - 1)] ,

где Xmax – конечное значение диапазона измерения,

Х – текущее значение измеряемой величины;

с и d – относительные постоянные величины.

Класс точности указывается либо на шкале прибора, либо в паспорте данного СИ. В таблице 2.2 приведены возможные варианты обозначений классов точности (цифровые значения даны в качестве примера).

Таблица 2.2. Обозначения классов точности

№ п/п	Пример обозначе- ния класса точности	Предел допускаемой погрешности	Форма выражения погрешности
	0, 5	γ = ± 0, 5%	Максимальная относительная приведённая погрешность, где Хн – диапазон в единицах измеряемой величины
	1,0	γ =± 1%	То же, но диапазон равен длине шкалы или её рабочей части
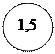
		δд = ± 1, 5 %	Постоянная относительная погрешность. Тогда Δд=δд· Х/100
	0,5/0,1	δд = ± [0, 5+0,1·(Xmax/X-1)]	Относительная погрешность, возрастающая с уменьшением измеряемой величины
	А, В или С	Значение погрешности рассчитывается по формулам, приведённым в документации (ГОСТе) на данное СИ	Максимальная абсолютная погрешность ± Δд. На СИ указана одна из данных латинских букв

Из обозначений классов точности, приведённых в табл. 2.2, наиболее часто встречаются обозначения № 1, 4 и 5.

В соответствии с ГОСТ 8.401-80 значения классов точности должны соответствовать следующему нормальному ряду:

n

(1; 1,5; 2 ; 2,5; 4; 5; 6)· 10 , где n = -3; -2; -1; 0.

2.3 Расчёт основных погрешностей измерительных цепей

Автоматизированная система контроля (АСК) состоит из измерительных цепей включающих в себя измерительный преобразователь, нормирующий или промежуточный преобразователь, вторичный прибор и/или аналого-цифровой (АЦП) преобразователь для выхода на ЭВМ. Поэтому возникает необходимость в расчёте суммарных основных погрешностей таких комплектов, а также выборе диапазонов измерений или преобразования измерительных устройств.

При выборе диапазона измерения (преобразования)руководствуются следующими соображениями:

1. Если известно рабочее (номинальное) значение Xnom измеряемого технологического параметра, то диапазон

D = Xmax – Xmin , при Xmin = 0 определяется как

D = Xnom /0.7 (2.1)

2. Если выбирается прибор (преобразователь) с безнулевой шкалой (диапазон преобразования), т. е.

D =Xmax – Xmin при Xmin ≠ 0, то рабочее значение измеряемого параметра может находиться посередине диапазона.

3. Значение диапазона D выбирается из нормальных рядов, в соответствии с расчитанным по формуле (2.1).

При расчёте суммарных основных погрешностей измерительных цепей при отсутствии корреляции пользуются формулой геометрического суммирования:

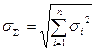
где 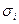- погрешность i -го преобразователя (прибора), которая может быть представлена в абсолютном, относительном или приведённом виде.