Оценка трудоемкости сортировки

Оценим трудоемкость процесса упорядочения массива из N ключей. В исходном состоянии эти ключи могут образовывать любую из N! перестановок. Энтропия массива ключей, определяемая по Шеннону:

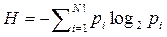
где p_i – вероятность перестановки с номером i. Наибольшей энтропией обладает система, для которой все состояния равновероятны: 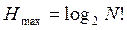. Для упорядоченной таблицы, все ключи которой различны, энтропия равна нулю. Изменение энтропии равно количеству информации, получаемой в процессе сортировки. Для случайного массива необходимо получить 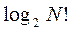бит информации. При сравнении ключей K_i, K_jможем получить два исхода: K_i<K_j и K_i>K_{j .} (случаем К_i=K_j пренебрегаем, как маловероятным).

Если исходы равновероятны, то сравнение дает ровно 1 бит информации. Такие ключи называют статистически эквивалентными. Если исходы неравновероятны, то будет получено меньше одного бита информации. Кстати, именно из-за того, что некоторые сортировки сравнивают статистически неэквивалентные ключи, они имеют низкую эффективность.

Таким образом, число сравнений ключей при сортировке удовлетворяет неравенству

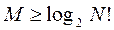
Для вычисления N! воспользуемся формулой Стирлинга

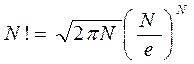
С учетом этого после преобразований получим

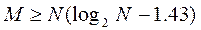
Найденная оценка 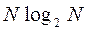будет служить ориентиром при оценке эффективности различных методов сортировки.