Квадратичный выбор
 |
Быстродействие сортировки выбором можно улучшить, если сделать процесс выбора многоступенчатым. Пусть размер таблицы N=16. Разобьем таблицу на 4 группы по 4 элемента в каждой, как на рис 32
Рис 32. Квадратичный выбор
Определим наибольший элемент в каждой группе и поместим его в отдельную группу "лидеров". Наибольший среди них и есть наибольший в таблице. Поместим его в область вывода. Последующие элементы отыскиваются так: среди элементов группы, из которой происходил выбранный на предыдущем шаге элемент, выбираем наибольший и помещаем вместо выбывшего в группу лидеров. Затем очередной элемент выводится из группы лидеров. Если N – точный квадрат, то можно разделить таблицу на 
групп по элементов. Любой выбор, кроме первого потребует не более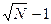 
сравнений внутри группы ранее выбранного элемента плюс 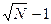сравнений внутри группы лидеров. Таким образом, время такой сортировки пропорционально 
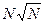, что гораздо лучше N2. Эту идею можно обобщить, получив метод кубического выбора, выбора четвертой степени и т.д.
Кубический выбор состоит в том, чтобы разделить таблицу на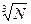 
больших групп, каждая из которых состоит из 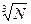малых групп по 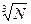элементов. Время такой сортировки пропорционально 
. Если развить эту идею до ее полного завершения, когда в группе на каждом уровне содержится только два элемента, то придем к методу, основанному на выборе из бинарного дерева.
Дата добавления: 2014-12-02; просмотров: 748;