Обход бинарного дерева

Для работы с древовидными структурами имеется множество алгоритмов, и многие из них используют одну и ту же идею, а именно идею прохождения или обхода дерева. Обход дерева подразумевает такой порядок работы с его узлами, для которого каждый из них посещается точно один раз. Для обхода бинарного дерева могут быть использованы три способа, определяемых рекурсивно.

Прямой обход.

1. Обработать корень

2. Обойти левое поддерево

3. Обойти правое поддерево

Обратный обход.

1. Обойти левое поддерево

2. Обработать корень

3. Обойти правое поддерево

Концевой обход.

1. Обойти левое поддерево

2. Обойти правое поддерево

3. Обработать корень

Рис. 22 Варианты обхода бинарного дерева.

На рис. 23 изображено бинарное дерево и порядок следования его узлов для различных методов обхода.

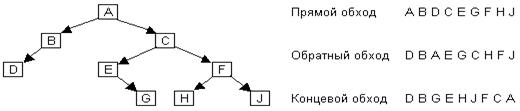
Рис 23. Бинарное дерево и варианты его обхода

Ниже приводится текст рекурсивной функции, выполняющей обход дерева в прямом порядке.

void DirectBypass(NODE *Root){

// Root – указатель на корень дерева

if(Root==NULL) return; // дерево пусто

Обработка(Root); // делаем то, что нужно с узлом

DirectBypass(Root->Llink); // пройти левое поддерево

DirectBypass(Root->Rlink); // пройти левое поддерево

}

Обратный и концевой обходы отличаются только местоположением оператора Обработка(Root)среди остальных.

Идея реализации алгоритма с "ручным" ведения стека (это может потребоваться, если язык не допускает рекурсии) заключается в том, что мы запоминаем в стеке историю спуска по левым ветвям дерева для того, чтобы впоследствии можно было вернуться и обработать оставшиеся узлы. Ниже приведен текст функции, выполняющей обход в обратном порядке.

const int MAXSTACK=50;

void InverseBypass(NODE *Root){

// Нерекурсивный обход бинарного дерева

NODE *stack[MAXSTACK];

NODE *s;

int v=0; // указатель на вершину стека

s=Root;

again:

if(s!=NULL){

// спускаемся по левым ветвям, запоминая историю в стеке

stack[v++]=s;

s=s->Llink;