Микроскопические сечения выведения для гомогенных сред
(en >1 МэВ) s, 10-24 см2
| Материал | s | Материал | s |
| Берилий | 0,9 | Титан | 1,7 ± 0,05 |
| Углерод | 0,72 ± 0,05 | Железо | 1,9 ± 0,1 |
| Водород | 1,00 ± 0,05 | Цирконий | 2,37 ± 0,05 |
| Литий | 0,9 ± 0,05 | Свинец | 3,60 ± 0,20 |
| Кислород | 0,87 ± 0,05 |
Таблица П.37
Эллиптические интегралы первого рода F(k,J)[16], k = sina

| 00 | 200 | 400 | 600 | 700 | ||
| 00 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | ||
| 400 | 0,6981 | 0,7043 | 0,7213 | 0,7436 | 0,7535 | ||
| 600 | 1,0472 | 1,0660 | 1,1226 | 1,2126 | 1,2619 | ||
| 800 | 1,3963 | 1,4344 | 1,5597 | 1,8125 | 2,0119 |
ОТВЕТЫ И РЕШЕНИЯ
1.1.Согласно формуле (1.13), активность 1 г 226Ra A = 3,66×1010 Бк @ 1 Ки[17]; активность 1 г 238U А @ 3,36×10-7 Ки = 1,24×104 Бк. Таким образом, активность 1 г 226Ra в ~ 3×106 раз больше активности 1 г 238U.
1.2.а) l = 1,6×10-5 с-1; Т1/2=0,5 сут;
б) l = 1,16×10-9 с-1; Т1/2=6930сут.
1.3.Масса образца, содержащего естественный уран, может быть записана через массы составляющих его изотопов урана m1(238U), m2(235U), m3(234U): m = m1 + m2 + m3, причем
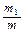 = 0,99275;
= 0,99275; 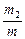 = 0,0072;
= 0,0072; 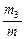 = 5,0×10-5. Учитывая, что активность обусловлена всеми тремя радионуклидами урана, запишем, используя формулу (1.13),
= 5,0×10-5. Учитывая, что активность обусловлена всеми тремя радионуклидами урана, запишем, используя формулу (1.13),
А = 1,13×1013 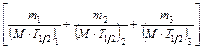 , тогда
, тогда
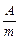 = 6,63×10-7 Ки/г, отсюда, если А = 1 Ки, то m@1,5×106 г.
= 6,63×10-7 Ки/г, отсюда, если А = 1 Ки, то m@1,5×106 г.
1.4.а)4,36×10-9 г; б) 161 г.
1.5.5,45×10-5 %.
1.6.Содержание КвKCl составляет 0,527 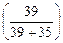 . В 1 г KCl содержится 0,527 г К или 6,22×10-5 г 40К (0,527×0,000118). Из формулы (1.13) активность А одного грамма 40К равна 1,6×104 Бк/кг.
. В 1 г KCl содержится 0,527 г К или 6,22×10-5 г 40К (0,527×0,000118). Из формулы (1.13) активность А одного грамма 40К равна 1,6×104 Бк/кг.
1.7.5,88×108 Бк.
1.8.2,42 мг.
1.9.Из формул (1.5) и (1.6) получаем, что за время t (4,5×109 лет) число распавшихся атомов урана составит DNU = 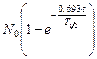 , где N0 - начальное число ядер урана, Т1/2 - период полураспада 238U. Так как масса одного атома в граммах составляет ma =
, где N0 - начальное число ядер урана, Т1/2 - период полураспада 238U. Так как масса одного атома в граммах составляет ma = 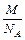 (NA – число Авогадро, M – атомная масса), то в m кг 238U число атомов 238U составит
(NA – число Авогадро, M – атомная масса), то в m кг 238U число атомов 238U составит 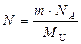 (в начальный момент времени, когда mU = 1 кг, N = N0). Поскольку в цепочке распада ядер 238U все радионуклиды имеют период полураспада, значительно меньший, чем возраст Земли, то можно полагать, что за рассматриваемый период времени накопится столько же ядер 206Pb, сколько распалось ядер 238U. Масса ядер свинца составит
(в начальный момент времени, когда mU = 1 кг, N = N0). Поскольку в цепочке распада ядер 238U все радионуклиды имеют период полураспада, значительно меньший, чем возраст Земли, то можно полагать, что за рассматриваемый период времени накопится столько же ядер 206Pb, сколько распалось ядер 238U. Масса ядер свинца составит
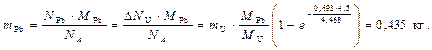 1.10.Содержание 14С в живых деревьях примерно постоянно; оно начинает уменьшаться только с гибелью дерева за счет распада 14С. За время t, прошедшее с момента гибели дерева, активность 14С уменьшится в е-lt раз и составит 0,9 от равновесной активности 14С живого дерева А0:
1.10.Содержание 14С в живых деревьях примерно постоянно; оно начинает уменьшаться только с гибелью дерева за счет распада 14С. За время t, прошедшее с момента гибели дерева, активность 14С уменьшится в е-lt раз и составит 0,9 от равновесной активности 14С живого дерева А0: 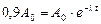 . Время t, прошедшее с момента гибели дерева, и есть возраст деревянного предмета t @ 870 лет.
. Время t, прошедшее с момента гибели дерева, и есть возраст деревянного предмета t @ 870 лет.
1.11.5,83×1020 атомов.
 1.12.Активность радионуклида А связана с числом q испускаемых g-квантов соотношением (1.1), в данном случае q= А×[h(1,116 МэВ) + h(0,511 МэВ)] = А×(0,507 + 2×0,0146). Отсюда активность А = 9,32×107 Бк.
1.12.Активность радионуклида А связана с числом q испускаемых g-квантов соотношением (1.1), в данном случае q= А×[h(1,116 МэВ) + h(0,511 МэВ)] = А×(0,507 + 2×0,0146). Отсюда активность А = 9,32×107 Бк.
1.13.h(0,6 МэВ) = 0,12;
h(0,5 МэВ) = 0,23× 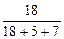 = 0,138;
= 0,138;
h(2 МэВ) = 0,23×  = 0,0383;
= 0,0383;
h(2,75 МэВ) = 0,0537;
|
 + 0,138×
+ 0,138×  = 0,308;
= 0,308;
h(2,25 МэВ) = 0,11; h(0,75 МэВ) = 0,716.
1.14.См. рис. О.1.
1.15. См. рис. О.2. eg1 =eb2 - eb1 = 0,2 МэВ;
eg2 =eb3 - eb1 = 0,7 МэВ; eg3 =eb3 - eb2 = 0,5 МэВ.
 |
1.16.Аннигиляционные фотоны образуются после торможения позитрона в веществе источника, т.е. при b+-распаде. Если радионуклид 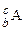 - чистый излучатель аннигиляционных фотонов, значит, все позитроны поглощаются в источнике. Когда происходит только b+-распад (100 %) (рис. О.3 а), при аннигиляции позитрона испускается два g-кванта с энергиями по 0,511 МэВ, в этом случае внешний выход g-квантов составляет 200 %. Если же выход аннигиляционных фотонов составляет 150 %, значит, вероятность b+-распада составляет не 100, а 75 %, т.е. остальные 25 % ядерных превращений приходятся на другие способы распада. Способ распада, который не сопровождается испусканием какого-либо излучения и также приводит к образованию ядра
- чистый излучатель аннигиляционных фотонов, значит, все позитроны поглощаются в источнике. Когда происходит только b+-распад (100 %) (рис. О.3 а), при аннигиляции позитрона испускается два g-кванта с энергиями по 0,511 МэВ, в этом случае внешний выход g-квантов составляет 200 %. Если же выход аннигиляционных фотонов составляет 150 %, значит, вероятность b+-распада составляет не 100, а 75 %, т.е. остальные 25 % ядерных превращений приходятся на другие способы распада. Способ распада, который не сопровождается испусканием какого-либо излучения и также приводит к образованию ядра 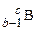 , - это электронный захват (рис. О.3 б). Таким образом, в случае б) на электронный захват приходится 25 % ядерных превращений, а на b+-распад – 75 % ядерных превращений.
, - это электронный захват (рис. О.3 б). Таким образом, в случае б) на электронный захват приходится 25 % ядерных превращений, а на b+-распад – 75 % ядерных превращений.
|


1.17. Через время t число ядер радионуклида А1 будет равно  . Изменение числа ядер нуклида А2 составит
. Изменение числа ядер нуклида А2 составит 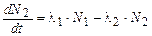 . Получается линейное дифференциальное уравнение
. Получается линейное дифференциальное уравнение 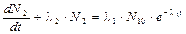 , решение которого можно найти в виде[18] N2(t) =
, решение которого можно найти в виде[18] N2(t) = 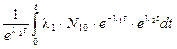 =
=
= l1×N10× 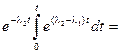
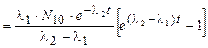
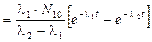 .
.
1.18.Для двух радионуклидов законизменения активности дочерних радионуклидов выражается формулой (1.10). Продифференцировав N2(t) по dt и приравняв производную нулю, получим время t = 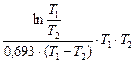 = 17,5 ч.
= 17,5 ч.
1.19.АRa(0) @ 3×107 Бк (используется формула (1.10)).
1.20.За время облучения t0 при изменяющейся со временем плотности потока j(t) флюенс, согласно формуле (1.18), составит Ф = 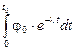 =
= 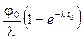 = 4,67×1012 1/см2.
= 4,67×1012 1/см2.
1.21. АV @6,3×102 Бк/м3.
1.22.АV @ 9,7 Бк/л.
1.23.j @ 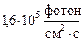 . Здесь учтено, что в источнике 60Со испускается два g-кванта на распад (1173 и 1333 кэВ), оба с вероятностью 100 %.
. Здесь учтено, что в источнике 60Со испускается два g-кванта на распад (1173 и 1333 кэВ), оба с вероятностью 100 %.
1.24.Активность А связана с числом радиоактивных ядер N формулой (1.3). Скорость счета nсч связана с активностью образца А соотношением nсч = А×x×hb = N×l×x×hb, где l - постоянная распада радионуклида; x - эффективность регистрации; hb - выход b-частиц. Отсюда число радиоактивных ядер 90Y 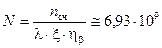 (hb и Т1/2 см. в табл. П.4).
(hb и Т1/2 см. в табл. П.4).
1.25.  @4,49 МэВ; De @ 8,98 МэВ.
@4,49 МэВ; De @ 8,98 МэВ.
 1.26.Число q g-квантов, испускаемых изотропным источником активностью А в единицу времени, определяется формулой (1.1). Число g-квантов, падающих на поверхность детектора, заключенную в телесный угол DW, составит Dq =
1.26.Число q g-квантов, испускаемых изотропным источником активностью А в единицу времени, определяется формулой (1.1). Число g-квантов, падающих на поверхность детектора, заключенную в телесный угол DW, составит Dq = 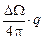 , где DW – телесный угол, под которым детектор «видит» источник (рис. О.4). По определению телесного угла[19], DW =
, где DW – телесный угол, под которым детектор «видит» источник (рис. О.4). По определению телесного угла[19], DW = 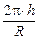 , где R – радиус шара, h – высота шарового сегмента (h = R – l). Радиус шара R =
, где R – радиус шара, h – высота шарового сегмента (h = R – l). Радиус шара R = 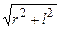 , тогда
, тогда 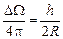 и Dq =
и Dq = 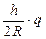 . Отсюда активность источника А =
. Отсюда активность источника А = 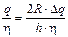 @ 4,7×105 Бк. Задача решается проще, если предположить, что плотность потока в любой точке диска одинакова. Это предположение практически верно, поскольку r << l. Тогда поток на поверхности F @ j×S = j×pr2, где j – плотность потока в центре диска. Для точечного изотропного источника плотность потока находится по формуле (1.17), отсюда активность A@
@ 4,7×105 Бк. Задача решается проще, если предположить, что плотность потока в любой точке диска одинакова. Это предположение практически верно, поскольку r << l. Тогда поток на поверхности F @ j×S = j×pr2, где j – плотность потока в центре диска. Для точечного изотропного источника плотность потока находится по формуле (1.17), отсюда активность A@ 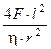 @4,7×105 Бк.
@4,7×105 Бк.
1.27.2,9×108 Бк (необходимо учесть радиоактивный распад атомов источника за время облучения).
1.28.1,1×109 1/см2.
2.1.1). По определению 1 Р = 1 ед. СГС/см3. Так как 1 Кл = 3×109 ед. СГС и масса 1 см3 воздуха составляет m = 1,293×10-3 г (m = V×r = = 1 см3×1,293×10-3 г/см3), то 1 Р = 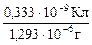 = 2,58×10-4 Кл/кг.
= 2,58×10-4 Кл/кг.
2). Заряд образующихся в воздухе ионов равен заряду электрона е = 1,602×10-19 Кл. Доза 1 Р означает, что в 1 см3 образуется заряд, равный Q = 1 ед. СГС = 0,333×10-10 Кл. Число пар ионов Nион, возникающих в 1 см3 воздуха, равно отношению общего заряда к заряду одного иона:
Nион = 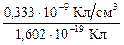 = 2,08×109 пар ионов/см3.
= 2,08×109 пар ионов/см3.
3). В 1 г воздуха образуется Nион = 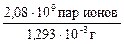 ==1,61×1012 пар ионов/г.
==1,61×1012 пар ионов/г.
4). На создание одной пары ионов в воздухе требуется в среднем 33,85 эВ. При образовании 2,08×109 пар ионов в 1 см3 воздуха поглотится энергияe = 2,08×109 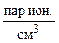 ×33,85×10-6 МэВ = 7,05×104 МэВ/см3 = 5,45×107 МэВ/г.
×33,85×10-6 МэВ = 7,05×104 МэВ/см3 = 5,45×107 МэВ/г.
5). Учитывая, что 1 МэВ = 1,602×10-13 Дж, получим 1 Р = 8,73×10-3 Дж/кг (Гр).
2.2. Воздушная керма Ка определяется в соответствии с формулой (2.11). Учитывая, что на образование одной пары ионов в воздухе расходуется энергия » 34 эВ, получим за год 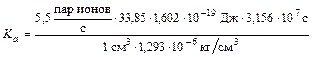 @ 7,3×10-4 Гр.
@ 7,3×10-4 Гр.
2.3.Из таблицы П.7 следует, что характеристическое излучение КХ 137Cs+140mBa имеет энергии eg1 = 0,03219 МэВ (h = 0,0392) и eg2 = 0,03182 МэВ (h = 0,0213). Интерполируя данные табл. П.9, находим массовые коэффициенты поглощения энергии для воздуха: 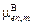 (0,03219 МэВ) @ 0,0132 м2/кг;
(0,03219 МэВ) @ 0,0132 м2/кг; 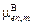 (0,03182 МэВ)@ 0,0135 м2/кг (для нахождения воздушной кермы по формуле (2.27) требуется массовый коэффициент передачи энергии
(0,03182 МэВ)@ 0,0135 м2/кг (для нахождения воздушной кермы по формуле (2.27) требуется массовый коэффициент передачи энергии 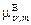 , но для радионуклидных источников, когда eg £ 3 МэВ,
, но для радионуклидных источников, когда eg £ 3 МэВ, 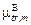 @
@ 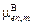 ). Керма-постоянная равна мощности воздушной кермы на расстоянии 1 м от точечного изотропного источника активностью 1 Бк, и для источника со сложным энергетическим составом определяется по формуле (2.34). Найдем
). Керма-постоянная равна мощности воздушной кермы на расстоянии 1 м от точечного изотропного источника активностью 1 Бк, и для источника со сложным энергетическим составом определяется по формуле (2.34). Найдем 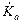 на расстоянии 1 м от источника активностью 1 Бк:
на расстоянии 1 м от источника активностью 1 Бк:
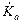 =
= 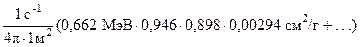 = =21,4×10-18 Гр/c. Согласно формуле (2.30), керма-постоянная ГК = 21,4
= =21,4×10-18 Гр/c. Согласно формуле (2.30), керма-постоянная ГК = 21,4 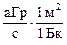 = 21,4 аГр×м2/(с×Бк).
= 21,4 аГр×м2/(с×Бк).
2.4.Квантовые выходы гамма-линий составляют: h(2 МэВ) = 0,98×0,9 = 0,882; h(0,5 МэВ) = h(1,5 МэВ) = 0,098. Для расчета ионизационной гамма-постоянной ГХ находим мощность экспозиционной дозы 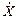 на расстоянии 1см от источника активностью 1 мКи (формула (2.27)):
на расстоянии 1см от источника активностью 1 мКи (формула (2.27)):
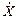 =
= 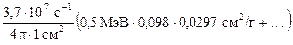 = 9,0 Р/ч.
= 9,0 Р/ч.
ГХ = 9,0 Р×см2/(ч×мКи).
2.5.23,4 аГр×м2/(с×Бк).
2.6.6,06 Р×см2/(ч×мКи).
2.7.35,6 аГр×м2/(с×Бк) (учтено образование двух аннигиляционных гамма-квантов с энергией по 0,511 МэВ).
2.8.ГК @ 120 аГр×м2/(с×Бк); ГХ @ 18,2 Р×см2/(ч×мКи).
2.9.5,1аГр×м2/(с×Бк).
2.10.0,775Р×см2/(ч×мКи).
2.11.ГК = 1,16 аГр×м2/(с×Бк); ГХ = 0,176 Р×см2/(ч×мКи).
2.12.31,9 аГр×м2/(с×Бк).
2.13.87,9 мР/ч.
2.14.0,232 мГр/ч.
2.15.Источник 51Cr имеет Т1/2 = 27,7 сут (табл. П.7), поэтому в расчетах флюенса необходимо учитывать распад источника за время наблюдения t0: Ф = 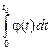 =
= 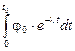 =
= 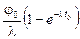 , где j0 - плотность потока в начальный момент времени, l - постоянная распада. Тогда Ка = 426 мкГр.
, где j0 - плотность потока в начальный момент времени, l - постоянная распада. Тогда Ка = 426 мкГр.
2.16.Меньшую мощность воздушной кермы создает нуклид 137Cs.
2.17.1,66 мкГр/ч.
2.18. 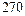 мкГр/ч.
мкГр/ч.
2.19.Используя формулы (2.23) и (1.17), получим
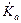 = 0,00279
= 0,00279 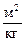 ×1,602×10-13 Дж×
×1,602×10-13 Дж× 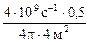 = 64 мкГр/ч.
= 64 мкГр/ч.
Задачу можно также решить по-другому: найти керма-постоянную, т.е. мощность воздушной кермы на расстоянии 1 м от источника активностью 1 Бк (формула 2.23): 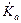 = 1,78×10-17 Гр/с, тогда ГК = 17,8 аГр×м2/(с×Бк). По формуле (2.32)
= 1,78×10-17 Гр/с, тогда ГК = 17,8 аГр×м2/(с×Бк). По формуле (2.32) 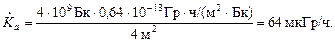
2.20.25,8 см.
2.21.I = 2,8×106 МэВ/(см2×с); j = 6,93×106 1/(см2×с).
2.22.4,63 Р/ч.
2.23.Мощность экспозиционной дозы на расстоянии r от точечного изотропного источника определяется формулой (2.33). Поскольку по условию величины мощностей экспозиционных доз от источников 60Со и 226Ra равны, можно записать АСо×ГХ(Со) = АRa×ГХ(Ra). Отсюда АСо = АRa× 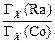 . Так как в табл. П.7 даны только керма-постоянные источников ГК, для нахождения ионизационных постоянных ГХ для источников 60Со и 226Ra используется соотношение (2.36). Тогда АСо = 0,65 мКи.
. Так как в табл. П.7 даны только керма-постоянные источников ГК, для нахождения ионизационных постоянных ГХ для источников 60Со и 226Ra используется соотношение (2.36). Тогда АСо = 0,65 мКи.
2.24.Из формулы (2.37) ke = 5,22 нГр×м2/с.
2.25. 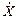 = 33,6 Р/ч;
= 33,6 Р/ч; 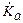 = 294 мГр/ч.
= 294 мГр/ч.
2.26.1,63 мкГр/с (для решения используется формула (2.40) и энергетический эквивалент рентгена 1 Р ® 8,73×10-3 Гр)×
2.27. 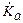 = 13,3 нГр/с;
= 13,3 нГр/с; 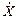 = 5,5 мР/ч.
= 5,5 мР/ч.
2.28.2×103 нГр×м2/с.
2.29.Поглощенная доза находится по формулам (2.42) – (2.46) при z = 0,1 г/см2: D(z) = 2,67×10-9 . Радионуклид 131I испускает 0,894 b-частицы на один распад, т.е. 894 b-частицы в секунду (формула (1.1)). Мощность поглощенной дозы, обусловленная этими b-частицами, составит
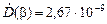 Гр/b-част.
Гр/b-част. 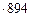 b-част./с @ 2,4 мкГр/с.
b-част./с @ 2,4 мкГр/с.
2.30.Мощность поглощенной дозы g-квантов для точечного изотропного источника можно найти по формулам (2.25) и (1.17); значение массового коэффициента поглощения для биологической ткани находится интерполяцией данных, представленных в табл. П.9: 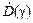 =
= 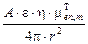 = 1,22×10-8 Гр/с. Соотношение дозы b- и g-излучения составляет в данном случае
= 1,22×10-8 Гр/с. Соотношение дозы b- и g-излучения составляет в данном случае 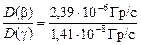 @ 196 (ослабление потока g-квантов в ткани не учитывается, для пути 1 мм оно невелико:
@ 196 (ослабление потока g-квантов в ткани не учитывается, для пути 1 мм оно невелико: 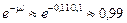 ; здесь m - линейный коэффициент ослабления, l = 1 мм).
; здесь m - линейный коэффициент ослабления, l = 1 мм).
3.1. Соотношение между поглощенной и экспозиционной дозами в воздухе определяется формулой (2.26), т.е. при Х = 1 Р DВ = 1 Р 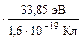 = 2,58×10-4
= 2,58×10-4  = 8,73×10-3 Гр (здесь 33,85 эВ – средняя энергия ионообразования в воздухе). Тогда поглощенная доза в ткани DТ (формула (2.20)) будет равна DТ @ DВ×1,09 = 9,5×10-3 Гр.
= 8,73×10-3 Гр (здесь 33,85 эВ – средняя энергия ионообразования в воздухе). Тогда поглощенная доза в ткани DТ (формула (2.20)) будет равна DТ @ DВ×1,09 = 9,5×10-3 Гр.
Задача решается проще, если использовать энергетический эквивалент рентгена: 1 Р ® 8,73×10-3 Гр. Тогда можно сразу записать поглощенную дозу в воздухе DВ = 8,73 мГр.
3.2.Для тепловых нейтронов взвешивающий коэффициент излучения wR = 5 (табл. П.11), следовательно, эквивалентная доза, создаваемая тепловыми нейтронами в ткани, согласно формуле (3.4), Нт.н. = 500 мкЗв. Одинаковые биологические эффекты соответствуют одинаковым эквивалентным дозам, поэтому для g-квантов эквивалентная доза тоже равна 500 мкЗв. Так как для фотонов wg = 1, то соответствующая по биологическому эффекту поглощенная доза в ткани фотонного излучения составит Dg = 500 мкГр. Для a-частиц D a = 25 мкГр.
3.3.25,7 мкЗв.
3.4.23 мкЗв.
3.5. 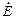 @ 0,32 мкЗв/с;
@ 0,32 мкЗв/с; 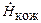 @ 0,37 мкЗв/с. Для расчета используются формулы (3.12) и (3.14), дозовые коэффициенты представлены в табл. П.13 и П.14.
@ 0,37 мкЗв/с. Для расчета используются формулы (3.12) и (3.14), дозовые коэффициенты представлены в табл. П.13 и П.14.
3.6.46,2 мкЗв (формула (3.12) и табл. П.13).
3.7.Нкож @ 2 мЗв. В задаче учтено, что источник 60Со испускает два g-кванта на один распад со средней энергией 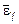 = 1,25 МэВ с вероятностью 100 % (каждый); 54Mn испускает один g-квант с энергией 0,835 МэВ на один распад. Отсюда плотность потока на рабочем месте для g-квантов с энергией 0,835 МэВ j1 =
= 1,25 МэВ с вероятностью 100 % (каждый); 54Mn испускает один g-квант с энергией 0,835 МэВ на один распад. Отсюда плотность потока на рабочем месте для g-квантов с энергией 0,835 МэВ j1 = 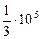 фотон/(см2×с), для
фотон/(см2×с), для 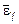 = 1,25 МэВ j2 =
= 1,25 МэВ j2 = 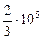 фотон/(см2×с).
фотон/(см2×с).
3.8.1,2 мкЗв/ч (табл. П.17).
3.9.0,207 мЗв (табл. П.4 и П.16).
3.10.Время работы персонала гр. А составляет 1700 часов в год (табл. П.22).За год экспозиционная доза составит X = 0,15×10-3 Р/ч× ×1700 ч = 0,255 Р. В условиях равновесия заряженных частиц, пренебрегая энергией электронов и позитронов, затрачиваемой на образование тормозного излучения в воздухе, можно считать, что энергетически поглощенная доза в воздухе эквивалентна экспозиционной дозе, т.е. можно использовать энергетический эквивалент рентгена (1 Р ® 8,73×10-3 Гр) для определения поглощенной дозы в воздухе, тогда DВ = = 2,23×10-3 Гр. Согласно формуле (2.20), поглощенная доза в биологической ткани (в точке) составит DТ @ 1,09×DВ = 2,43 мГр. Эквивалентная доза облучения фотонным излучением органа или ткани НТ = 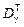 ×wg = 2,45 мГр×1 Зв/Гр = 2,43 мЗв. Эффективная доза при равномерном облучении всех органов (формула (3.6)) Е @ 2,4 мЗв.
×wg = 2,45 мГр×1 Зв/Гр = 2,43 мЗв. Эффективная доза при равномерном облучении всех органов (формула (3.6)) Е @ 2,4 мЗв.
3.11.Используя энергетический эквивалент рентгена (при условии электронного равновесия), можно найти мощность воздушной кермы 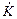 = 0,15×10-3×8,73×10-3 Гр/ч = 1,31×10-6 Гр/ч. Из соотношения (3.2), используя значения керма-коэффициента dК (табл. П.13), можно найти плотность потока j =
= 0,15×10-3×8,73×10-3 Гр/ч = 1,31×10-6 Гр/ч. Из соотношения (3.2), используя значения керма-коэффициента dК (табл. П.13), можно найти плотность потока j = 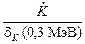 = 0,95×106 фотон/(см2×с). Тогда эффективная доза (считаем облучение изотропным) за год будет равна Е = =j×t×dЕ(0,3 МэВ; ИЗО) = 0,95×106
= 0,95×106 фотон/(см2×с). Тогда эффективная доза (считаем облучение изотропным) за год будет равна Е = =j×t×dЕ(0,3 МэВ; ИЗО) = 0,95×106 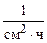 ×1700 ч×0,916×10-12 Зв×см2 @ @1,5 мЗв (формула (3.13) и табл. П.13), т.е. значение, рассчитанное для конкретной ситуации (дана энергия фотонов), меньше, чем полученная в задаче № 3.10 верхняя граница значения эффективной дозы (2,4 мЗв).
×1700 ч×0,916×10-12 Зв×см2 @ @1,5 мЗв (формула (3.13) и табл. П.13), т.е. значение, рассчитанное для конкретной ситуации (дана энергия фотонов), меньше, чем полученная в задаче № 3.10 верхняя граница значения эффективной дозы (2,4 мЗв).
3.12.В условиях электронного равновесия заряженных частиц поглощенная доза практически совпадает с кермой. В таблице П.13 керма в воздухе на единичный флюенс dК(1 МэВ) = 4,47×10-12 Гр×см2, отсюда плотность потока j = 1864 фотон/(см2×с). Мощность эффективной дозы с учетом дозового коэффициента dЕ для энергии g-квантов 1 МэВ и геометрии ИЗО (табл. П.13) находится по формуле (3.12) и составляет 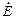 = dЕ(1 МэВ, ИЗО)×j = 21,5 мкЗв/ч.
= dЕ(1 МэВ, ИЗО)×j = 21,5 мкЗв/ч.
3.13.На расстоянии 4 м поток можно полагать близким к плоскопараллельному, поэтому нужно воспользоваться дозовыми коэффициентами табл. П.13 для геометрии облучения ПЗ; 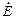 = 0,193 мкЗв/ч.
= 0,193 мкЗв/ч.
3.14.Из формулы (2.23) можно найти плотность потока фотонов j ( 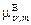 в табл. П.9), из табл. П.13 - дозовый коэффициент dЕ (0,5 МэВ, ПЗ). Эффективная доза (формула (3.13) Е =
в табл. П.9), из табл. П.13 - дозовый коэффициент dЕ (0,5 МэВ, ПЗ). Эффективная доза (формула (3.13) Е = 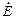 × t = j×t×dЕ (0,5 МэВ, ПЗ) = 374 мкЗв. Плотность потока фотонов j также может быть получена по формуле (3.2) через керма-коэффициент dК (табл. П.13).
× t = j×t×dЕ (0,5 МэВ, ПЗ) = 374 мкЗв. Плотность потока фотонов j также может быть получена по формуле (3.2) через керма-коэффициент dК (табл. П.13).
3.15.Флюенс Ф g-квантов можно найти либо из формулы (2.16), либо, используя энергетический эквивалент рентгена, из формулы (3.2). Массовые коэффициенты передачи энергии – в табл. П.9, воздушная керма на единичный флюенс dК (0,3 МэВ) – в табл. П.13. Для тепловых нейтронов дозовый коэффициент – в табл. П.17, тогда эффективная доза при заданном флюенсе нейтронов находится по формуле (3.13). Суммарная эффективная доза смешанного облучения Е = Еg + Еn @ 583 мкЗв.
3.16.11,4.
3.17.78,7 мкЗв.
3.18.254 мкЗв.
3.19.Флюенс за три часа находится по формуле (1.18), эффективная доза Е1 @ 3,4 мЗв. Если аналогичные измерения проводятся через неделю, то Е2 = 2,85 мЗв.
3.20.30,8 мЗв.
3.21.8,46×10-12 Гр/с; 51,7 мкЗв.
3.22.39 мкЗв (с учетом распада 203Hg).
3.23.7,2 мЗв (табл. П.7 и П.13).
3.24. 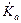 @ 1,1 мГр/ч;
@ 1,1 мГр/ч; 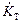 @ 1,22 мГр/ч; Е = 23,2 нЗв.
@ 1,22 мГр/ч; Е = 23,2 нЗв.
3.25.12,2 мЗв.
3.26.Если источник испускает g-кванты с различными энергиями, то эффективная доза будет равна Е =  , где ei, Фi - энергия и флюенс g-квантов определенной энергетической группы, i – число энергетических групп. Е = 1,73 мЗв.
, где ei, Фi - энергия и флюенс g-квантов определенной энергетической группы, i – число энергетических групп. Е = 1,73 мЗв.
3.27.При равномерном распределении дозы в течение года допустимая мощность эффективной дозы составляет 11,8 мкЗв/ч 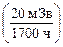 для персонала гр. А. В данном случае по формуле (2.40) можно найти мощность экспозиционной дозы
для персонала гр. А. В данном случае по формуле (2.40) можно найти мощность экспозиционной дозы 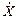 , затем, используя энергетический эквивалент рентгена -
, затем, используя энергетический эквивалент рентгена - 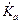 . Плотность потока j вычисляется по формуле (3.2), мощность эффективной дозы
. Плотность потока j вычисляется по формуле (3.2), мощность эффективной дозы 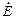 - по формуле (3.12):
- по формуле (3.12): 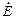 @ 0,57 мкЗв/ч. Работать в таких условиях можно.
@ 0,57 мкЗв/ч. Работать в таких условиях можно.
3.28.Работать можно (Е @ 16,3 мЗв за год).
3.29.Допустимый дозовый предел будет превышен (для решения задачи используются данные табл. П.4 и П.16).
3.30.Плотность потока на рабочем месте, согласно формуле (1.17), j @ 1,7×103 фотон/(см2×с). Допустимая плотность потока для персонала гр. А и 36-часовой рабочей недели 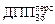 (0,662 МэВ; ИЗО) = 1,56×103 фотон/(см2×с). Если персонал гр. А работает 12 часов в неделю, то допустимая плотность потока на рабочем месте может быть больше
(0,662 МэВ; ИЗО) = 1,56×103 фотон/(см2×с). Если персонал гр. А работает 12 часов в неделю, то допустимая плотность потока на рабочем месте может быть больше 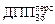 во столько раз, во сколько раз 36 часов больше числа часов реальной работы в неделю, т.е.
во столько раз, во сколько раз 36 часов больше числа часов реальной работы в неделю, т.е. 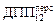 = =
= = 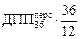 = 4,68×103 фотон/(см2×с). Допустимая плотность потока для персонала гр. Б в четыре раза меньше:
= 4,68×103 фотон/(см2×с). Допустимая плотность потока для персонала гр. Б в четыре раза меньше: 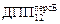 = 1,17×103 фотон/(см2×с). Так как плотность потока на рабочем месте j @ 1,7×103 фотон/(см2×с) больше 1,17×103 фотон/(см2×с), то можно сделать вывод, что работать в таких условиях нельзя.
= 1,17×103 фотон/(см2×с). Так как плотность потока на рабочем месте j @ 1,7×103 фотон/(см2×с) больше 1,17×103 фотон/(см2×с), то можно сделать вывод, что работать в таких условиях нельзя.
3.31.Активность источника можно найти из формулы (2.32). Для данной геометрии облучения ДППперс(0,662 МэВ, ПЗ) = =1,04×103 фотон/(см2×с) (табл. П.13). Используя формулу (1.17) для точечного изотропного источника, r = 123 см.
3.32.16 мин.
3.33.123 см.
3.34.7,2×1011 Бк/кг. Для проведения оценочных расчетов, пробу почвы можно считать точечным изотропным источником (если сравнить размеры пробы с расстоянием до рабочего места).
3.35.6,92×108 Бк.
3.36.0,6 Бк/м3 ( табл. П.19).
3.37.По формуле (1.13) можно найти величину поступившей активности. В таблице П.19 - значения дозовых коэффициентов 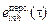 для малорастворимых соединений 60Со и 58Со. По формуле (3.8) находится ожидаемая эффективная доза внутреннего облучения как сумма поступления в организм активности Iinh малорастворимых соединений 60Со и 58Со: Е(t) @ 0,3 Зв. Концепция эффективной дозы применяется только для значений эффективных доз Е £ 0,1 – 0,2 Зв. Так как полученное значение эффективной дозы Е > 0,2 Зв, очевидно, что концепция эффективной дозы в данном случае неприемлема! Работник получил слишком большую дозу облучения (годовой предел дозы для персонала группы А составляет 50 мЗв), и дальнейшие действия в отношении данного работника определяются регламентом действий службы радиационной безопасности на данном предприятии.
для малорастворимых соединений 60Со и 58Со. По формуле (3.8) находится ожидаемая эффективная доза внутреннего облучения как сумма поступления в организм активности Iinh малорастворимых соединений 60Со и 58Со: Е(t) @ 0,3 Зв. Концепция эффективной дозы применяется только для значений эффективных доз Е £ 0,1 – 0,2 Зв. Так как полученное значение эффективной дозы Е > 0,2 Зв, очевидно, что концепция эффективной дозы в данном случае неприемлема! Работник получил слишком большую дозу облучения (годовой предел дозы для персонала группы А составляет 50 мЗв), и дальнейшие действия в отношении данного работника определяются регламентом действий службы радиационной безопасности на данном предприятии.
3.38.Ожидаемая эффективная доза внутреннего облучения составит Е(t) = 2 мЗв. Поскольку соединения типа «М» имеют значительно большее время растворения в легких, чем период полураспада 58Со (70,8 сут), можно считать, что основную дозу облучения получили легкие, т.е. ожидаемая эквивалентная доза в легких Hлегк.(t) @ Е(t)/w легк. = 16,7 мЗв (wТ в табл. П.12).
3.39.Объемная концентрация 131I в помещении составляет 2,5×108 Бк/м3, причем аэрозоли составляют 108 Бк/м3. Стандартная скорость дыхания (табл. П.22) составляет 0,0235 м3/мин 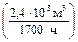 . Оператор за пять минут вдохнет объем воздуха, равный V = 0,1175 м3, получив таким образом внутрь активность 131I Iing = 1,2×107 Бк. Ожидаемая эффективная доза внутреннего облучения при ингаляционном поступлении 1 Бк 131I для соединений типа «Б»
. Оператор за пять минут вдохнет объем воздуха, равный V = 0,1175 м3, получив таким образом внутрь активность 131I Iing = 1,2×107 Бк. Ожидаемая эффективная доза внутреннего облучения при ингаляционном поступлении 1 Бк 131I для соединений типа «Б» 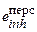 (131I) = 7,6×10-9 Зв/Бк (табл. П.19), тогда, согласно формуле (3.8), Е (t) @ 90 мЗв.
(131I) = 7,6×10-9 Зв/Бк (табл. П.19), тогда, согласно формуле (3.8), Е (t) @ 90 мЗв.
3.40.В щитовидную железу попала активность А = 1,25×106 Бк. Число распавшихся атомов 131I, согласно формуле(1.3), равно N = 1,25×1012. Энергия, выделившаяся при распаде N атомов, составит eb = 1,25×1012 ×0,181 МэВ/расп. = 0,0361 Дж, тогда поглощенная доза в щитовидной железе (масса 20 г), в соответствии с формулой (2.17), будет равна Dщж= 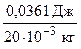 @ 1,8 Гр. Нщж @ 1,8 Зв (формула (3.4) и табл. П.11).
@ 1,8 Гр. Нщж @ 1,8 Зв (формула (3.4) и табл. П.11).
3.41.1,4 мЗв (см. табл. П.22 и П.19).
3.42.Состав естественного урана приведен в табл. П.5., активность изотопов урана находится по формуле (1.13). Ожидаемая эффективная доза внутреннего облучения рассчитывается по формуле (3.8) с использованием данных табл. П.19 и составляет 0,19 мЗв.
3.43.Из таблицы П.18 можно определить, что окислы плутония относятся к малорастворимым соединениям. Ожидаемая эффективная доза Е(t) = 59,3 мЗв, что превышает годовой дозовый предел для персонала группы А.
3.44.Содержание 60Со в воде превышает допустимый уровень и употреблять населению эту воду нельзя (табл. П.21).
3.45.Вода данного водоема непригодна для употребления населением. Оценка допустимости использования воды для питья проводится в соответствии с формулой (3.10); уровни вмешательства УВвода представлены табл. П.21.
3.46.Персонал гр. А может работать в данном помещении в течение года по два часа в неделю.
 |
4.1.Рассмотрим элемент поверхности диска в виде кругового кольца ds, находящийся на расстоянии r от центра диска (рис. О.5). Его площадь ds = 2π×r×dr[20]. Этот элемент поверхности испускает qs×ds g-квантов, обусловливая плотность потока в точке Р, равную
 , где х – расстояние от точки Р до элемента поверхности ds,
, где х – расстояние от точки Р до элемента поверхности ds,  .
.
Плотность потока в точке Р от всего диска равна
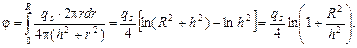 [21]
[21]
|
|
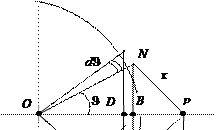
 , где х – расстояние от точки Р до шарового слоя ds (на рис. О.6 отрезок PN).
, где х – расстояние от точки Р до шарового слоя ds (на рис. О.6 отрезок PN).
Кривая боковая поверхность шарового слоя ds равна произведению высоты слоя BD на длину окружности с радиусом, равным радиусу шара: ds = 2pR×BD. Из рисунка О.6: OB = R×cosJ; OD = =R×cos(J+dJ); BD = OB - OD = R×[cosJ - cos(J+dJ)] = = 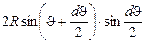 »
» 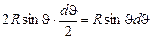 = -R×d(cosJ). Тогда ds = -2p×R2×d(cosJ). В DPNO по теореме косинусов x2 = r2 + R2 - 2Rr×cosJ, откуда cosJ =
= -R×d(cosJ). Тогда ds = -2p×R2×d(cosJ). В DPNO по теореме косинусов x2 = r2 + R2 - 2Rr×cosJ, откуда cosJ = 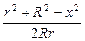 , а производная cosJ по х равна
, а производная cosJ по х равна 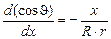 . Максимальное значение, которое может принимать х, равно xmax=
. Максимальное значение, которое может принимать х, равно xmax=  , а минимальное xmin = r - R. Таким образом, полная плотность потока j в точке Р будет равна
, а минимальное xmin = r - R. Таким образом, полная плотность потока j в точке Р будет равна
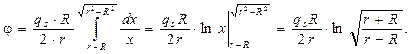
 4.3.Элемент излучающей поверхности ds сферического поверхностного источника (рис. О.6) можно записать в виде ds = -2p×R2×d(cosJ) (см. решение задачи 4.2). Тогда dj =
4.3.Элемент излучающей поверхности ds сферического поверхностного источника (рис. О.6) можно записать в виде ds = -2p×R2×d(cosJ) (см. решение задачи 4.2). Тогда dj = 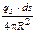 = -
= - 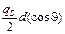 . При изменении J от 0 до π cosJ изменяется от 1 до -1, следовательно, плотность потока в центре сферы равна j = =
. При изменении J от 0 до π cosJ изменяется от 1 до -1, следовательно, плотность потока в центре сферы равна j = = 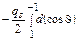 = qs. Чтобы найти мощность воздушной кермы
= qs. Чтобы найти мощность воздушной кермы 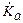 , необходимо воспользоваться формулой (4.1), где в выражении для плотности потока j поверхностная мощность источника qs заменена на поверхностную активность Аs:
, необходимо воспользоваться формулой (4.1), где в выражении для плотности потока j поверхностная мощность источника qs заменена на поверхностную активность Аs: 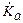 = 4p×ГК×j(qs ® Аs) = =4p×ГК××Аs. Таким образом, видно, что
= 4p×ГК×j(qs ® Аs) = =4p×ГК××Аs. Таким образом, видно, что 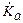 в центре сферы не зависит от радиуса сферы и полной активности источника.
в центре сферы не зависит от радиуса сферы и полной активности источника.
 4.4.а). Точка Р расположена сбоку от источника (рис. О.7). Рассмотрим элемент dl линейного источника, находящегося на расстоянии l от точки O (отрезок ОА). Плотность потока g-квантов dj в точке Р, создаваемую элементом dl излучающей поверхности, можно записать как
4.4.а). Точка Р расположена сбоку от источника (рис. О.7). Рассмотрим элемент dl линейного источника, находящегося на расстоянии l от точки O (отрезок ОА). Плотность потока g-квантов dj в точке Р, создаваемую элементом dl излучающей поверхности, можно записать как 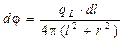 , а плотность потока от всего линейного источника
, а плотность потока от всего линейного источника
j=  =
= 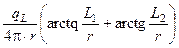 [22].
[22].
 Если L1 = L2, то j==
Если L1 = L2, то j== 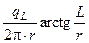 .
.
б). Точка Р находится на оси источника (рис. О.8). Тогда 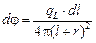 , а полная плотность потока
, а полная плотность потока  [23].
[23].
в). Плотность потока в точке Р (рис. 4.2), находящейся на высоте h над плоскостью, в которой расположен линейный источник, выражается интегралом 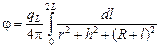 . Введя новую переменную x = l + R, получим j =
. Введя новую переменную x = l + R, получим j = 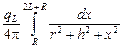 . После интегрирования получим формулу (4.4).
. После интегрирования получим формулу (4.4).
4.5.Для бесконечно длинного источника с линейной мощностью qL плотность потока g-квантов на расстоянии r от источника равна
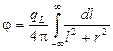 =
=  =
= 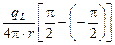 =
= 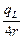 (см. задачу 4.4). В центре полуокружности радиусом r (рис. О.9) плотность потока g-квантов
(см. задачу 4.4). В центре полуокружности радиусом r (рис. О.9) плотность потока g-квантов 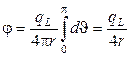 (линейный элемент dl @ r×dJ). Мощность воздушной кермы в обоих случаях будет одинакова:
(линейный элемент dl @ r×dJ). Мощность воздушной кермы в обоих случаях будет одинакова: 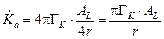 .
.
 4.6.Учитывая небольшой диаметр трубы по сравнению с линейными размерами трубопровода, можно рассматривать трубу как тонкий (линейный) источник в виде кольца. Тогда линейная активность источника АL будет связана с объемной АV соотношением
4.6.Учитывая небольшой диаметр трубы по сравнению с линейными размерами трубопровода, можно рассматривать трубу как тонкий (линейный) источник в виде кольца. Тогда линейная активность источника АL будет связана с объемной АV соотношением
AL = 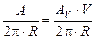 = πr2×AV = =7,85×103 Бк/м. Элемент окружности dl = 2R×sin
= πr2×AV = =7,85×103 Бк/м. Элемент окружности dl = 2R×sin 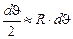 (при малых dJ). Тогда в центре кольца dj =
(при малых dJ). Тогда в центре кольца dj = 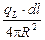 , а полная плотность потока в точке О (рис. О.9) j =
, а полная плотность потока в точке О (рис. О.9) j = 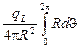 =
= 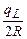 . Мощность воздушной кермы в воздухе в центре кольца, согласно формуле (4.1) (при замене qL на AL),
. Мощность воздушной кермы в воздухе в центре кольца, согласно формуле (4.1) (при замене qL на AL), 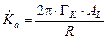 @ 5,0 нГр/ч.
@ 5,0 нГр/ч.
4.7.4,5 нГр/ч.
4.8.4,2 ×109 Бк.
4.9.35,2 мкР/ч.
4.10.1,8×107 Бк/м2.
4.11.0,8 мЗв.
4.12.3,1 нГр/ч.
4.13.Линейный керма-эквивалент keLсвязан с удельной (линейной) активностью AL и керма-постоянной ГК источника соотношением keL=  = AL×ГК. Плотность потока выражается формулой (4.12), а
= AL×ГК. Плотность потока выражается формулой (4.12), а 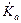 - формулой (4.1):
- формулой (4.1): 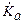 =4p×ГК×
=4p×ГК× 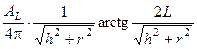 = 158 мкГр/ч.
= 158 мкГр/ч.
4.14.Поверхностный керма-эквивалент можно записать как kes = As×ГК (из формулы (2.37)), где Аs – поверхностная активность источника, ГК – керма-постоянная источника. Плотность потока над центром диска выражается формулой (4.12), тогда, согласно формуле (4.1), 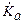 =1,02 мГр/ч.
=1,02 мГр/ч.
4.15.1,4 часа в день.
 |
4.16.Плотности потока dj g-квантов на оси источника от элемента излучающей поверхности ds равна
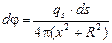 , где ds – элемент боковой поверхности ds, x – расстояние от точек Р1,2,3по оси цилиндра до элемента ds (рис. О.10). Элемент боковой поверхности ds = 2pR×dx, тогда
, где ds – элемент боковой поверхности ds, x – расстояние от точек Р1,2,3по оси цилиндра до элемента ds (рис. О.10). Элемент боковой поверхности ds = 2pR×dx, тогда 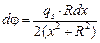 .
.
а). Плотность потока g-квантов в точке Р1 внутри цилиндра
j = 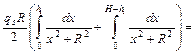 =
=  .
.
б). Если h1 = 0, то 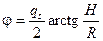 .
.
в). Точка Р3 находится вне цилиндрического источника на высоте h2 от его поверхности (рис. О.10), тогда
 .
.
4.17.Рассмотрим кольцевой элемент объема dV цилиндрического источника (рис. О.11): dV = ds×dx, где ds ≈ 2pr×dr – площадь кругового кольца, тогда dV = 2pr×dr×dx. Этот элемент объема dV создает в точке Р плотность потока g-квантов dj = 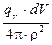 = =
= = 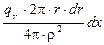 =
= 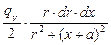 . Отсюда плотность потока g-квантов в точке Р от всего источника
. Отсюда плотность потока g-квантов в точке Р от всего источника
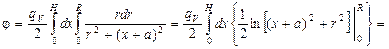
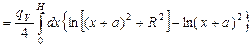 .
.
 |
Обозначим х + а = у, тогда
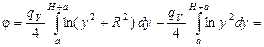
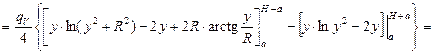
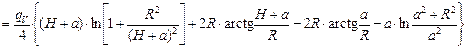 [24].
[24].
4.18.Элемент объема dV = 2pr×dr×dx (рис. О.12). Плотность потока первичных гамма-квантов в точке Р, обусловленная элементом излучающего объема dV, с учетом поглощения в источнике 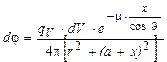
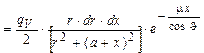 , где m – линейный коэффициент ослабления g-квантов в среде, J - угол видимости элемента ds из точки Р,
, где m – линейный коэффициент ослабления g-квантов в среде, J - угол видимости элемента ds из точки Р, 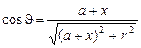 . Полная плотность потока в точке Р
. Полная плотность потока в точке Р 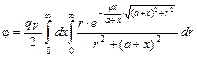 .
.
 |
Сделаем замену переменной:
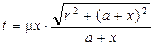 , тогда пределы интегрирования при r = 0 t = mx; при r = ¥ t = ¥. Запишем
, тогда пределы интегрирования при r = 0 t = mx; при r = ¥ t = ¥. Запишем 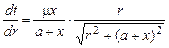 , отсюда
, отсюда 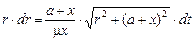 .
.
Тогда 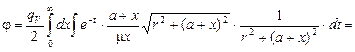
= 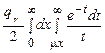 . Второй интеграл (по t) является интегральной показательной функцией E1(mx)[25]. Тогда, исходя из свойств интегральных показательных функций, j
. Второй интеграл (по t) является интегральной показательной функцией E1(mx)[25]. Тогда, исходя из свойств интегральных показательных функций, j 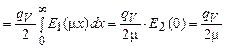 .
.
4.19.Поверхностный керма-эквивалент kes = 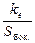 , где ke - общий керма-эквивалент, Sбок. – площадь боковой поверхности цилиндра, Sбок. = 2pR×H. Тогда, согласно формулам (4.1) и (4.19),
, где ke - общий керма-эквивалент, Sбок. – площадь боковой поверхности цилиндра, Sбок. = 2pR×H. Тогда, согласно формулам (4.1) и (4.19), 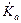 =4p×ГК×j(qs®Аs)= 4p×ГК×Аs×arctg1=4p×kes×
=4p×ГК×j(qs®Аs)= 4p×ГК×Аs×arctg1=4p×kes× 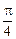 =
=  =0,314 Гр/с.
=0,314 Гр/с.
4.20.As = 7,15×107 Бк/м2; m = 9,23 мг.
4.21.а)2,6×10-12 Зв; б) 6,8×10-12 Зв (бесконечное полупространство – воздух, плотность потока j находится по формуле (4.22), линейный коэффициент поглощения men для воздуха - в табл. П.9).
4.22.1 мкЗв.
4.23.а) 0,23 мГр/ч; б) 0,56 мГр/ч – с учетом многократно рассеянного g-излучения в воде.
4.24.Плотность потока, создаваемая излучением боковой поверхности цилиндра, может быть найдено по формуле (4.15). Эллиптический интеграл F(  ,k) находится из табл. П.37 для углов
,k) находится из табл. П.37 для углов
J = arctg 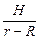 @ 400; k = arcsin
@ 400; k = arcsin 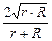 = 600.
= 600.
Тогда F(k = 600; J = 400) = 0,7436. Мощность воздушной кермы, обусловленная излучением боковой поверхности цилиндра, 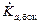 = 4pГК
= 4pГК 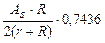 , где As – поверхностная активность. Мощность воздушной кермы, обусловленная излучением дна цилиндра, вычисляется по формуле (4.14). Поверхностная активность Аs, обусловленная излучением дна и стенок, составляет Аs @ 1,5×1010 Бк/м2.
, где As – поверхностная активность. Мощность воздушной кермы, обусловленная излучением дна цилиндра, вычисляется по формуле (4.14). Поверхностная активность Аs, обусловленная излучением дна и стенок, составляет Аs @ 1,5×1010 Бк/м2.
4.25. 0,22 мг.
4.26.0,47 нГр/ч.
5.1. m = ln5/d @ 1,6 см-1; eg @ 0,53 МэВ (табл. П.8).
5.2. 2,84.
5.3. Представим кратность ослабления в виде k = l×10m, где l = 1, m = 3. Тогда, согласно формуле (5.17), толщина защиты d = D1000 (Pb, εg = 0,662 МэВ) @ 73,7 г/см2 (табл. П.23), что с учетом плотности свинца (табл. П.3) составляет 6,5 см. Чтобы решить задачу по универсальным таблицам, необходимо учесть поправку на барьерность dD (табл. П.23), т.е. кратность ослабления kбар = 1000, которая задана для барьерной геометрии, нужно преобразовать в k для бесконечной геометрии k = 103×0,984 = 984. Для этого значения k из табл. П.29 находим d = 6,5 см.
5.4.73,1 см.
5.5.22,2 см.
5.6.а) 14,1 см по слоям ослабления; б) 13,8 см по универсальным таблицам.
5.7Кратность ослабления k = 2×103. Если известна величина слоя десятичного ослабления D1/10, то кратность ослабления можно рассчитать из соотношения k = 10n, где n – число слоев десятичного ослабления: 2×103 = 10n, откуда n = lg2×103. Таким образом, толщина защиты d = D1/10 ×n = 66 см.
5.8.Представим исходные данные в виде табл. О.1. В соответствии с определением керма-эквивалента (формула (2.37)) вклад рi каждой g-линии в керма-эквивалент составит рi = 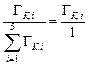 . Парциальная кратность ослабления g-излучения i-й энергетической группы равна ki = k×ni, т.е. k1= 0,5×103 = 500 и т.д.
. Парциальная кратность ослабления g-излучения i-й энергетической группы равна ki = k×ni, т.е. k1= 0,5×103 = 500 и т.д.
Таблица О.1
| ei, МэВ | ГК,i, аГр×м2/(с×Бк) | pi = 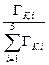
| ki = k×pi | di, см | D1/2, см |
| 0,1 | 0,5 | 0,5 | |||
| 0,2 | 0,2 | 0,2 | |||
| 0,4 | 0,1 | 0,1 | |||
| 0,8 (к) | 0,1 | 0,1 | |||
| 1,0 (г) | 0,1 | 0,1 |
По универсальным таблицам (табл. П.26) и полученным парциальным кратностям ослабления находим необходимые толщины защиты di для каждой линии. Из полученных данных видно, что главная линия – это линия с энергией εi5 = 1 МэВ, конкурирующая с энергией εi4 = 0,8 МэВ. Разность между толщинами защиты для главной и конкурирующей линий составит d = dгл – dк = 105 – 98 = 7 см.
По таблице П.26 определяются слои половинного ослабления главной и конкурирующей линий. Слой D1/2 для толщины d1 = 98 см, ослабляющей излучение в 100 раз, находится следующим образом: сначала по табл. П.26 определяется, какая толщина защиты требуется для ослабления излучения в k = 200 раз: d2 = 109 см; далее из толщины d2, ослабляющей излучение в 200 раз, вычитается толщина защиты d1, ослабляющая излучение в 100 раз, – это и будет слой половинного ослабления D1/2, ослабляющий излучение в два раза именно на этой толщине (d = 98 см). Таким образом, слой половинного ослабления конкурирующей линии D1/2к =d2-d1=109–98=11 см. Аналогично находится D1/2 для главной линии с εi5 = 1 МэВ: D1/2г = 117 – 105 = 12 см.
Окончательная толщина защиты определяется по формуле (5.11), поскольку значение D1/2max (12 см) больше разности d (7 см) между толщинами защит для главной и конкурирующей линий. Таким образом, искомая толщина защиты d = 110 см.
5.9.Для k = 25 d = 9,8 см; для k = 103 d = 22 см.
5.10.d = 69,7 см. Главная линия – с энергией 1,25 МэВ, конкурирующая – 0,835 МэВ. При решении необходимо использовать линейную интерполяцию для нахождения толщины защиты по табл. П.27.
5.11.Мощность воздушной кермы за защитой определяется по формуле (5.2), где G0 – мощность воздушной кермы без защиты (формула (2.32)). Используя данные табл. П.8 и П.25, получим 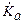 = 0,37 мкГр/с (при определении фактора накопления для md = 2,57 данные табл. П.25 необходимо интерполировать).
= 0,37 мкГр/с (при определении фактора накопления для md = 2,57 данные табл. П.25 необходимо интерполировать).
5.12.Из формулы (5.2) следует, что В = 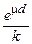 , где k – кратность ослабления. Толщина d находится из универсальных табл. П.26. Тогда В @ 6,8, с учетом барьерности Вбар. = 5,1. Фактор накопления, рассчитанный по формуле (5.3) (коэффициенты А, a1, a2 в табл. П.24), B(md) = 7,72; Вбар. = 5,8 (поправка на барьерность в табл. П.23). Отличие полученных результатов составляет ~ 12 %, что приемлемо при проведении расчетов по формуле (5.3).
, где k – кратность ослабления. Толщина d находится из универсальных табл. П.26. Тогда В @ 6,8, с учетом барьерности Вбар. = 5,1. Фактор накопления, рассчитанный по формуле (5.3) (коэффициенты А, a1, a2 в табл. П.24), B(md) = 7,72; Вбар. = 5,8 (поправка на барьерность в табл. П.23). Отличие полученных результатов составляет ~ 12 %, что приемлемо при проведении расчетов по формуле (5.3).
5.13.В @ 1,6 для g-квантов с энергией 2 МэВ; В @ 3,3 для энергии 0,5 МэВ (с учетом поправки на барьерность, табл. П.23). Начиная с энергии g-квантовeg @ 0,06 МэВ в алюминии преобладает процесс когерентного рассеяния, т.е. процессы поглощения g-квантов практически отсутствуют, фотоэффект уже закончился, а процесс образования пар еще не начинается. Поэтому в этой области энергий фактор накопления имеет такую же зависимость от энергии, как и сечение комптоновского рассеяния (уменьшается с ростом энергии g-кванта).
5.14.а) по универсальным таблицам (П.28) k = 2, kбар. = 2,26; б) по формуле (5.18) для однослойной защиты, с использованием табл. П.8, П.25 и П.23, k = 2,23.
5.15.d @ 23 см. Поскольку нуклид 59Fe имеет несколько g-линий, задача решается методом конкурирующих линий. Толщины di, необходимые для ослабления каждой i-ой линии, находятся по табл. П.29; для линий, имеющих небольшой вклад в дозу, толщина определяется приблизительно, т.к. слабые линии (по вкладу) обычно не участвуют в определении толщины защиты.
5.16.7,2 см.
5.17.54 см.
5.18.2,95 см.
5.19.По универсальным таблицам (табл. П.29) для защиты из свинца толщиной 3,6 см и энергии g-квантов 0,662 МэВ находится кратность ослабления, обеспечивающая допустимые уровни облучения персонала: k = 40. В новых условиях кра
Дата добавления: 2014-12-02; просмотров: 1607;

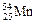 к задаче 1.14
к задаче 1.14
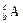 к задаче 1.16
к задаче 1.16