Подбор сечения верхней части колонны

Верхняя часть колонны согласно [6] должна рассчитываться на прочность или устойчивость при внецентренном сжатии и проектируется из прокатного двутавра.

Предварительно определяется требуемая площадь поперечного сечения двутавра, которая находится из условия его устойчивости в плоскости рамы (в плоскости действия момента) по формуле (109) [6]:

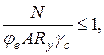
где N – продольное усилие, приложенное с эксцентриситетом e; γ_с=1,05 – коэффициент условий работы для колонн одноэтажных производственных зданий с мостовыми кранами, определяемый по табл. 1 [6]; φ_е - коэффициент устойчивости, принимаемый по табл. Д.3 [6] в зависимости от условной гибкости стержня

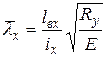
и приведенного относительного эксцентриситета

,

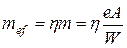причем W – момент сопротивления сечения для наиболее сжатого волокна, а η – коэффициент влияния формы сечения, определяемый по табл. Д.2 [6].

Для симметричного двутавра можно воспользоваться следующими приближенными зависимостями:

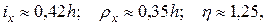
тогда

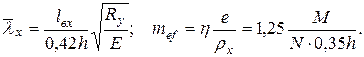
Определив условную гибкость и приведенный относительный эксцентриситет, находим коэффициент устойчивости и вычисляем требуемую площадь поперечного сечения двутавра. В рассматриваемом случае имеем:

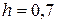м,

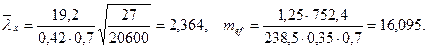
Коэффициент устойчивости φ_е=0,0806, а требуемая площадь поперечного сечения двутавра

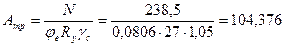(см²).

Несколько проще можно определить требуемую площадь сечения по следующей формуле

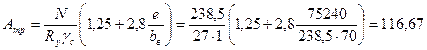(см²).

Кроме того, необходимо дополнительно отыскать требуемые радиусы инерции сечения, исходя из условия, что предельная гибкость стержня равна 120 ([6], табл. 32 при α=1):

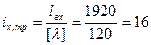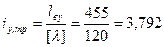(см); (см).

С учетом назначенной выше величины h_в=700мм, по сортаменту принимаем двутавр 70Б1 по ГОСТ 26020-83 с h=691мм, А=164,7см², J_x=125930см⁴, W_x=3645см³, i_x=27,65см, J_y=4556см⁴, i_y=5,26см, b_f=260мм, t_f=15,5мм, t_w=12мм, r₁=24мм.

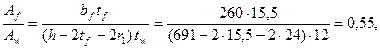
Последовательно вычисляе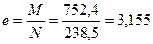м:

(м),

, ,

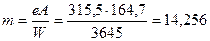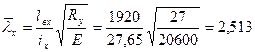по табл.Д.2 [6] ,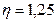

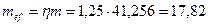, φ_е=0,073.

Проверяем устойчивость верхней части колонны в плоскости действия момента:

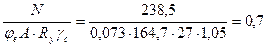< 1.

Устойчивость стержня обеспечена.

Предельная гибкость

.

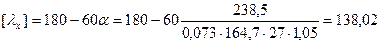Фактическая гибкость .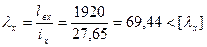

Переходим к проверке верхней части колонны из плоскости действия момента. Она выполняется по формуле (111) [6]:

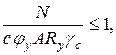
где коэффициент с определяется в зависимости от величины относительного эксцентриситета m_x, который, в свою очередь, принимается в соответствии с требованиями п. 9.2.5 и 9.2.6 [6].

В рассматриваемом случае 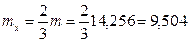(п.9.2.6 [6]), следовательно, с находится по формуле (112) [6]

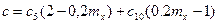
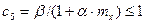
Для отыскания с необходимо предварительно вычислить ([6], п. 9.2.5, табл. 21):

; ,

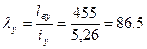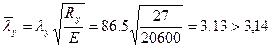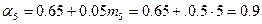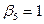, , φ_у=0,6164;

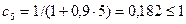
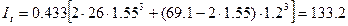(см⁴)

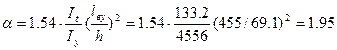
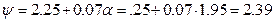
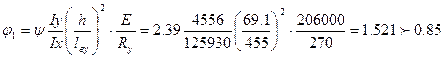
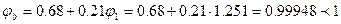
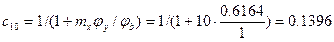
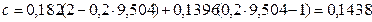
Проверяем устойчивость верхней части колонны из плоскости рамы

.

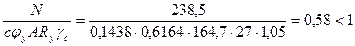Устойчивость верхней части колонны обеспечена.

В соответствии с требованиями п.9.4 [6] необходимо выполнить проверку устойчивости стенок и полок двутавра верхней части колонны. Вычисляем условную гибкость стенки (п. 9.4.2 [6]):

,

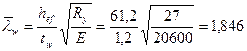причем h_ef 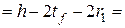69,1 – 2 · 1,55 – 2 · 2,4 = 61,2(см) (п.7.3.1 [6]). Поскольку в нашем случае 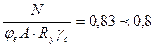предельную условную гибкость стенки следует определять по формуле (127) таблицы 22 [6] (см. п.9.4.3).

Наибольшее сжимающее напряжение у расчетной границы стенки

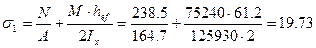(kH/см²)

Соответствующее напряжение у противоположной границы стенки

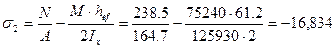(kH/см²)

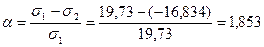
По таблице 17 определяем коэффициент с_cr в зависимости от α - с_cr=26,325

Среднее касательное напряжение в рассматриваемом сечении

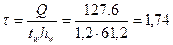(kH/см²)

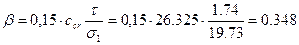
Предельная условная гибкость стенки

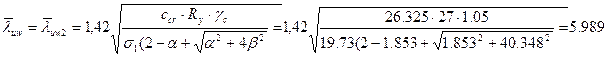
Согласно этой же формуле предельная условная гибкость стенки не может быть больше

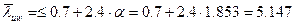
Окончательно 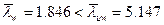– стенка устойчива.

Как указано в п.9.4.4 [6] стенку колонны при 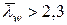следует, как правило, укреплять поперечными ребрами жесткости в соответствии с требованиями п.7.3.3 [6]. Очевидно, что в нашем случае этого делать не нужно.

В соответствии с требованиями п.9.4.7 устойчивость поясов (полок) внецентренно-сжатых (сжато-изгибаемых) стержней с гибкостью 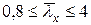следует считать обеспеченной, если условная гибкость свеса пояса (полки) 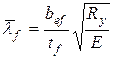не превышает значений предельной условной гибкости 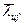, определяемых по формулам таблицы 23 [6]. Рассматриваемому случаю соответствует тип сечения 1 в таблице 23, когда 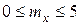, а в нашем случае m_x = 9,504, поэтому при определении предельной условной гибкости полки необходимо учитывать примечание к таблице 23. Последовательно определяем:

- предельное значение условной гибкости свеса пояса центрально-сжатого элемента, определяемое согласно требованиям п. 7.3.8 [6],

;

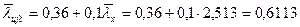- предельная условная гибкость полки по формуле (132) и m_x = 5

;

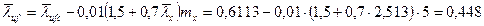- предельная условная гибкость полки по п 8.5.18 и m_x = 20

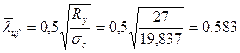
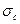- напряжение в сжатом поясе

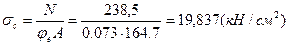
- предельная условная гибкость полки по интерполяции между двумя полученными значениями для m_x = 9,504 будет равна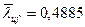

Расчетная ширина свеса полки b_ef определяется по п.7.3.7 [6], как расстояние от начала внутреннего закругления до края полки:

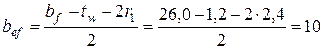(см).

Фактическая условная гибкость свеса пояса (полки)

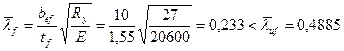– полка устойчива.

Следует заметить, что размеры прокатных двутавров, выпускаемых по отечественным нормативным документам, априори обеспечивают устойчивость их стенок и полок, и последние проверки можно было бы и не выполнять, однако в [6] нет никаких указаний на этот счет.