ОСНОВНЫЕ ПОНЯТИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ.
Часть Ш
Раздел 2
Задания и методические указания к решению задач для студентов заочного обучения 1-го курса всех специальностей
Н. Новгород









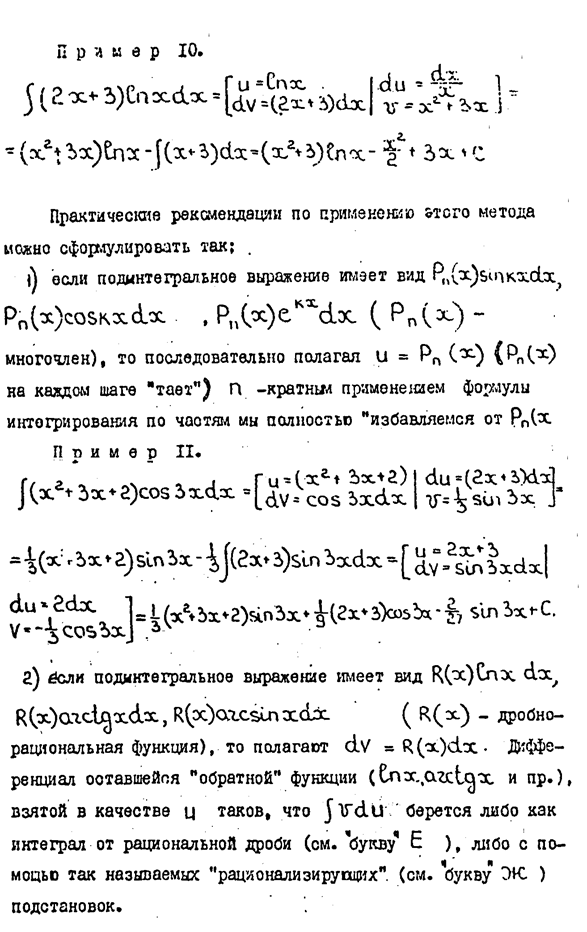


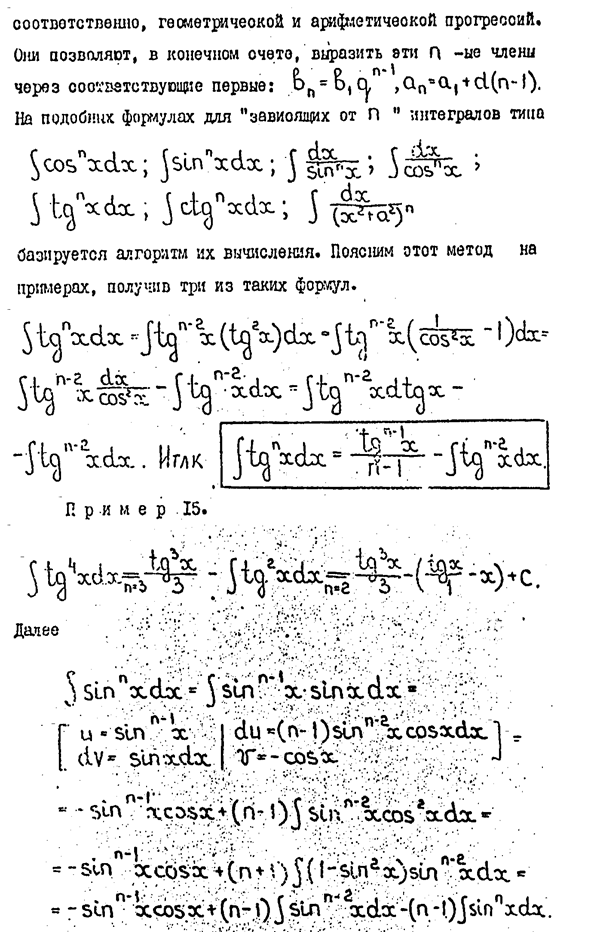
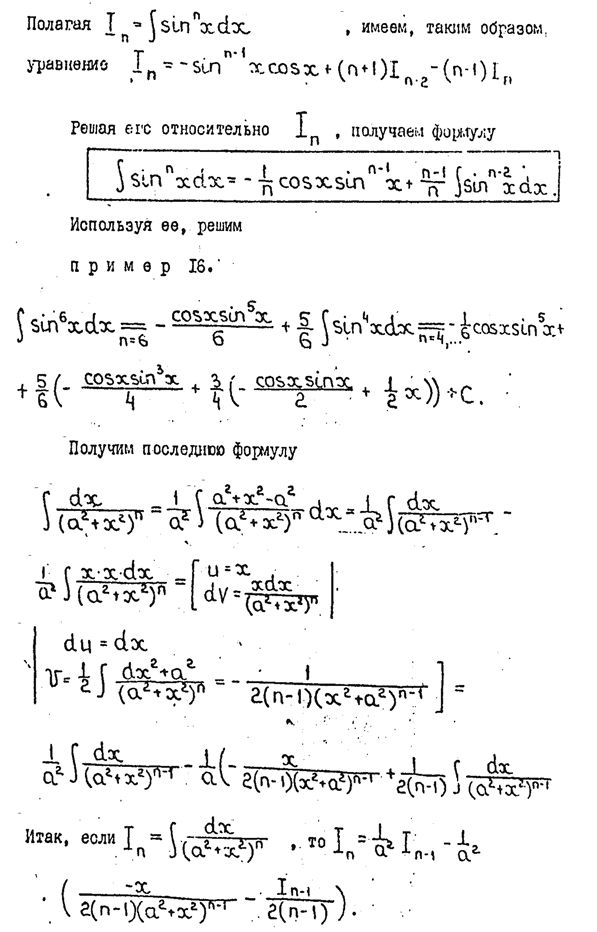







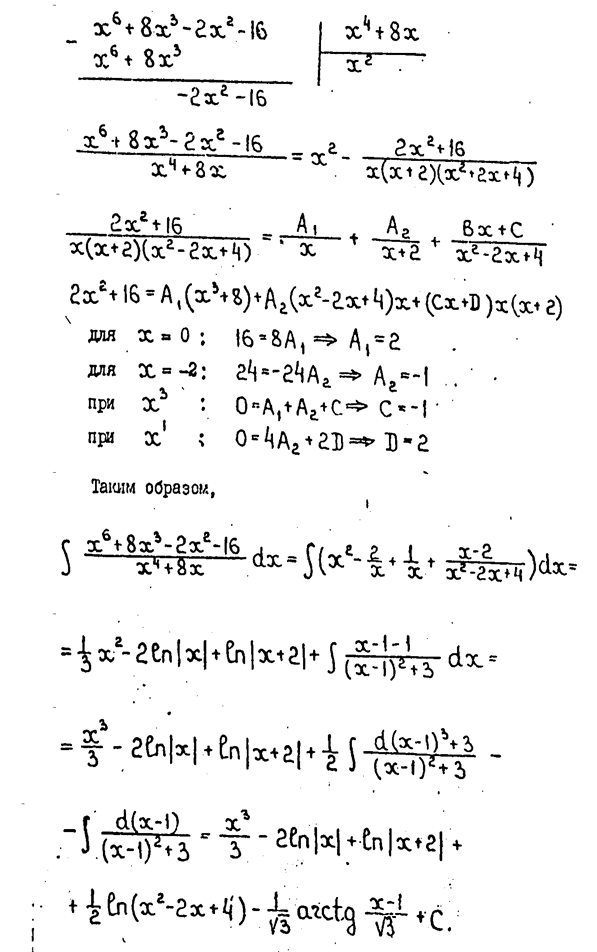

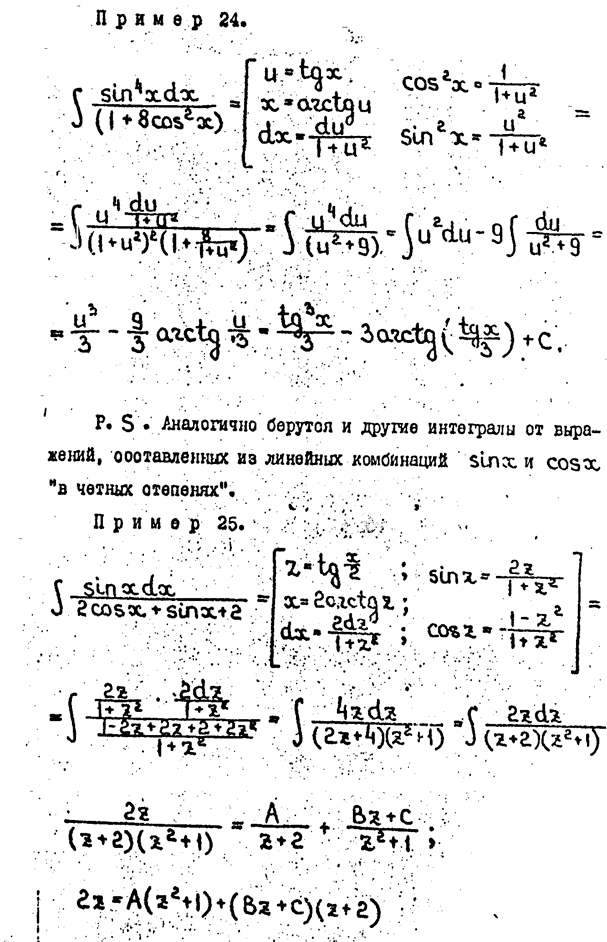


















ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ № 3
1. Найти неопределенные интегралы. В пп. 1) и 2) результаты проверить дифференцированием.
1. 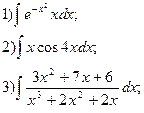 2.
2. 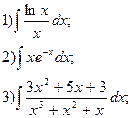
3. 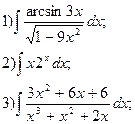 4.
4. 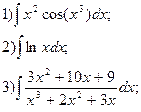
5. 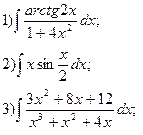 6.
6. 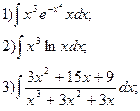
7. 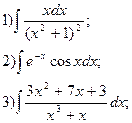 8.
8. 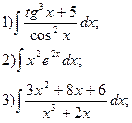
9. 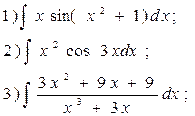 10.
10. 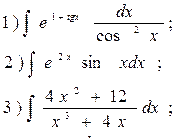
11. 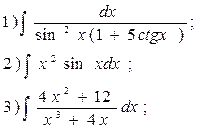 12.
12. 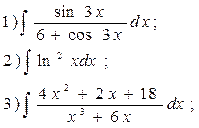
13. 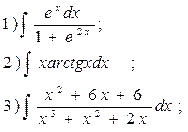 14.
14. 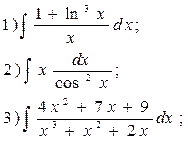
15. 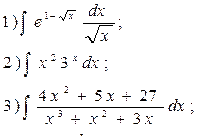 16.
16. 
17.  18.
18. 
19. 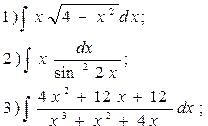 20.
20. 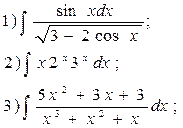
21. 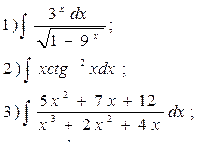 22.
22. 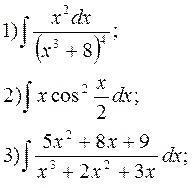
23. 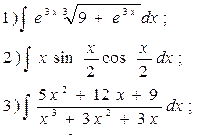 24.
24. 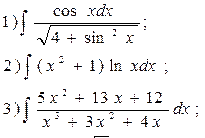
25. 
аОСНОВНЫЕ ВОПРОСЫ ПО КУРСУ «ОПРЕДЕЛЕННЫЙ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ»
1. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подставкой.
2. Интегрирование рациональных функций путем разложения на простейшие дроби. Интегрирование выражений, содержащий тригонометрические функции. Интегрирование некоторых иррациональных выражений.
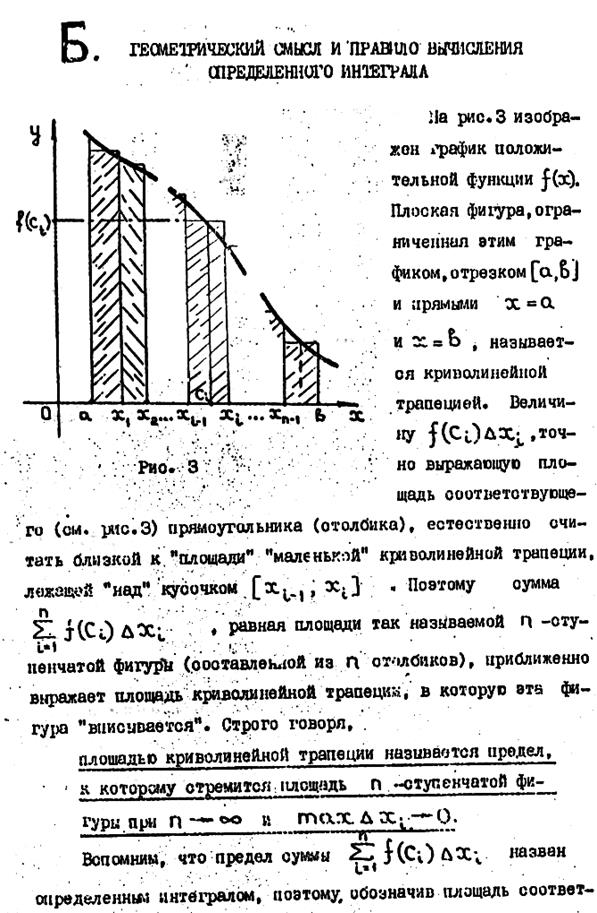
3. Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла.
4. Производная интеграла по верхнему пределу. Формула Ньютона – Лейбница.
5. Приближенное вычисление определенного интеграла: формула прямоугольников, трапеций и Симпсона.
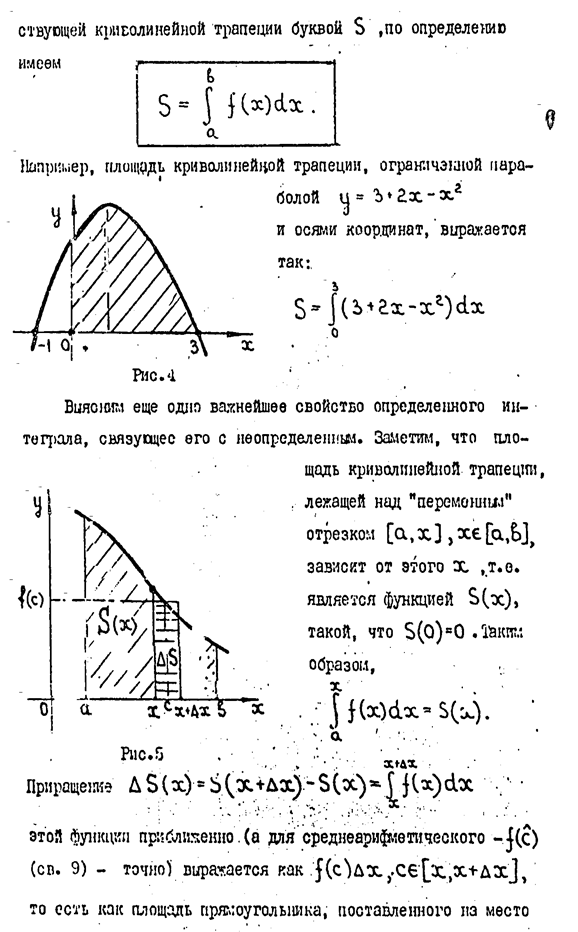
6. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов тел вращения.
7. Несобственные интегралы с бесконечными пределами. Несобственные интегралы от неограниченной функции.
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1. – М.: Наука, 1985.
2. Шипачев В.С. Высшая математика. / Под ред. акад. Тихонова А.Н. – М.: Высшая школа, 1985.
Дата добавления: 2014-12-01; просмотров: 1052;
