Задача 4.

Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. На следствии каждый из них сделал два заявления.

Браун. Я не делал этого.

Смит сделал это.

Джонс. Смит не виновен.

Браун сделал это.

Смит. Я не делал этого.

Джонс не делал этого.

Суд установил, что один из них дважды солгал, другой – дважды сказал правду, третий – один раз солгал, один раз сказал правду.

Кто совершил преступление?

Числа

Наиболее общие закономерности и законы экономических явлений выясняются путем качественного анализа, но конкретное выражение их возможно лишь с помощью меры и числа.

Число - важнейшее математическое понятие, меняющееся на протяжении веков. Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4…

При счете отдельных предметов единица есть наименьшее число, и делить ее на доли не нужно, а иногда и нельзя, однако уже при грубых измерениях величин приходится делить 1 на доли.

Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел. Дробью называется часть (доля) единицы или несколько равных ее частей.

Дроби обозначаются, как : 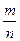, где m и n - целые числа;

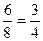- это сокращение дроби; а 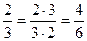- это расширение дроби.

Дроби со знаменателем 10 - это десятичные дроби: .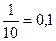

Среди десятичных дробей особое место занимают периодические дроби: 0,2525…=0,(25)= 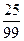- чистая периодическая дробь, 1,2555…=1,2(5)= 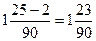- смешанная периодическая дробь.

Дальнейшее расширение понятия числа вызвано уже развитием самой математики (алгебры).

Декарт в 17 веке вводит понятие отрицательного числа. Числа целые (положительные и отрицательные), дробные (положительные и отрицательные) и нуль получили название рациональных чисел. Всякое рациональное число может быть записано в виде дроби конечной и периодической. Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа - введение действительных (вещественных) чисел - присоединением к рациональным числам иррациональных: иррациональные числа - это бесконечные десятичные непериодические дроби.

Иррациональные числа появились при измерении несоизмеримых отрезков (сторона и диагональ квадрата). В алгебре иррациональные числа появились при извлечении корней 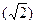. Примером трансцендентного, или иррационального числа являются числа π, е.

Все действительные числа можно изобразить на числовой оси. Числовая ось(числовая прямая) это:

а) горизонтальная прямая линия с выбранным на ней направлением;

б) на оси задано начало отсчета – нулевая точка 0;

в) на оси задана единица масштаба.

Х

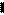
-2 -1 1 2 3