Теорема о движении центра масс механической системы

С теоремой об изменении количества движения непосредственно связана теорема о движении центра масс механической системы. Центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему: 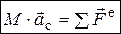. С учетом известных кинематических зависимостей (ч. 2, п. 2.2.3) то же векторое равенство в дифференциальной форме: 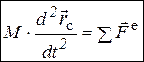, в проекциях на оси координат: , , .

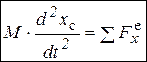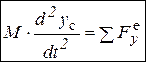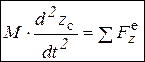Эти уравнения по форме такие же, как основное уравнение динамики (п. 3.1.2) и дифференциальные уравнения движения точки (п. 3.2.1). Поэтому подходы к исследованию движения центра масс механической системы могут быть такими же, как в динамике материальной точки.

По сути, теорема о движении центра масс – это лишь иная форма теоремы об изменении количества движения механической системы (п. 3.4.3). При решении многих задач они вполне заменяют друг друга. Тем не менее, некоторые следствия из теоремы о движении центра масс имеют важное практическое значение.

1. Из теоремы о движении центра масс вытекает закон сохранения движения центра масс механической системы: 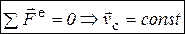, в проекции на любую ось 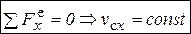(приведены только символические записи).

2. Поступательно движущееся тело в задачах динамики можно рассматривать как материальную точку.

3. Одни только внутренние силы не могут изменить характера движения центра масс системы, как не могут изменить и общего количества движения системы (п. 3.4.4).