Качество результата действия.

Что может делать данный объект? Рассмотрим этот вопрос на примере группы элементов, состоящей из трёх плоскостей (рис. 1А), свободно парящих в каком-либо пространстве и посмотрим на их взаимодействие между собой и пробным шаром.

Предположим, что у каждой из плоскостей возможны три результата действия:

 независимое движение в пространстве

 толкание других предметов

 соединение с другой плоскостью

А у шара есть только два возможных результата действия:

 независимое движение в пространстве

 толкание других предметов

Все три плоскости являются элементами группы и имеют совершенно одинаковые свойства (качества результата действия). Шар не принадлежит данной группе и мы его запускаем в игру только с одной целью – посмотреть, на что способна данная группа и каждый её элемент в отдельности?

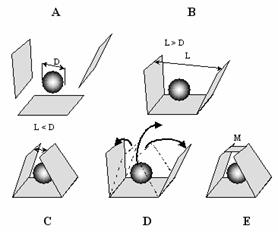
Рис. 1. Различные взаимодействия элементов.

И группа свободных элементов (А), и группа взаимодействующих элементов (В), при условии L>D, имеют одинаковый результат действия - толкают шар, но не лишают его свободы движения. При случайном уменьшении размера выхода полости по отношению к диаметру шара (С) возникнет ловушка для шара, но при его движении плоскости вновь могут разойтись и шар не лишается свободы движения (D). При постоянной фиксации выхода полости (перемычка M, на рис. D) шар вообще лишается свободы движения. При этом группа элементов из трёх плоскостей становится ловушкой для шара, т.е., у этой группы появляется цель – лишить шар свободы движения.

Шар и плоскости свободно двигаются в пространстве и толкают друг друга. При этом неважно, сколько плоскостей имеется в данном пространстве, одна или три, их количество не меняет их качества результатов действия. Все элементы сохраняют свои свойства и шар сохраняет свою способность свободно двигаться в пространстве. Все элементы группы взаимодействуют между собой. Суммарный результат их совместного действия и результат действия каждой отдельной плоскости всегда сохраняется один и тот же. В этом случае данная группа элементов не является системой, а является набором случайных отдельных элементов, поскольку как группа элементов, так и каждый из них в отдельности обладают одинаковыми результатами действия.

Изменим условия эксперимента и заставим плоскости взаимодействовать таким образом, чтобы их края, рёбра плоскостей, сцепились друг с другом (рис. 1В). В результате такого взаимодействия одно из свойств плоскостей было нейтрализовано (независимость движения), они стали двигаться в пространстве уже зависимо друг от друга и появилось новое пространство (полость), ограниченное плоскостями. Поместим внутрь его пробный шар.

Если размеры входа (выхода) новой полости больше диаметра шара (L > D, рис. 1В), то опять качественно ничего не изменилось, пробный шар по прежнему сохраняет свои результаты действия (может свободно двигаться). Но если размер выхода полости становится меньше диаметра шара (L < D, рис. 1С), то появляется качественно новое свойство – система из трёх взаимодействующих элементов превращается в ловушку для пробного шара, который лишается одного из своих свойств – свободно двигаться в пространстве. Причём случайное и однократное выполнение данного условия (L < D) не вызывает появление нового качества (рис. 1С), поскольку при движении шар раздвинет плоскости и уйдёт в пространство (рис. 3D). Только постоянное выполнение условия L < D превращает данную группу из простого набора элементов в группу с качественно новым признаком (рис. 1Е).

Новое качество может быть только у группы определённым образом взаимодействующих элементов. Определённый – значит целевой. Определённым образом взаимодействующих – это значит имеющих определённую цель, построенных определённым образом и действующих определённым образом для достижения данной цели. Его не может быть у отдельно взятых элементов, и у случайно взаимодействующих элементов. До выполнения этого условия группа элементов была бесцельно парящей в пространстве случайной группой плоскостей. После выполнения данного условия эта группа превратилась в новый элемент – ловушку для шара.

В результате определённого взаимодействия элементов часть их свойств нейтрализуется, а другая часть используется для достижения цели. Превращение одних форм материи в другие происходит именно за счёт нейтрализации каких-то свойств этих форм материи. А нейтрализация происходит за счёт изменения каких-либо связей между элементами объекта, потому что эти связи определяют форму объекта. Поэтому «нейтрализуется», но не «уничтожается», потому что ничто в этом мире не исчезает и не появляется (закон сохранения).

Целью любой системы является выполнение заданного (определённого) условия, достижение заданного результата действия (цели). Если заданный результат действия получился случайно, то в следующий момент он уже может не выполняться и заданный результат исчезнет. Но если для чего-то необходимо, чтобы результат действия всегда (постоянно) был именно такой, а не какой-либо иной (задание цели), необходимо, чтобы группа взаимодействующих элементов постоянно сохраняла этот новый результат действия. Для этого данная группа элементов должна постоянно стремиться сохранять заданное условие (выполнение цели). В примере с плоскостями и пробным шаром этим условием является соблюдение неравенства L < D, которое выполняется, например, перемычкой М (рис. 1Е), или соединив расходящиеся края плоскостей.

Таким образом, группа элементов из трёх плоскостей может быть системой для захвата пробного шара или любого другого тела подходящего размера, как может быть и системой для нашей демонстрации, только в том случае, если она может выполнить заданное условие (выполняет заданную цель). В данном случае, если целью группы из трёх плоскостей является захват какого-либо тела и эта группа может это сделать, она является системой.