Полимерное взаимодействие генов

Открытие Менделем основных законов наследственности оказалось возможным благодаря тому, что он анализировал контрастные, альтернативные признаки, которые легко различались между собой. Каждый признак (окраска цветка, форма и цвет горошины) определялся различными аллелями одного гена. Однако такие четко различимые альтернативные формы существуют не для всех признаков. Рост людей или высоту растений нельзя разделить только на два класса: высокие и низкие. Рост, вес, плодовитость, продолжительность жизни, длина колоса или метелки – это несколько примеров многочисленных признаков, для которых характерна непрерывная изменчивость. Непрерывная изменчивость обусловлена, во-первых, взаимодействием между различными генами и, во-вторых, взаимодействием между генами и окружающей средой (генотип × среда).

Признаки, которые можно измерить, подсчитать, взвесить называются количественными. Они контролируются многими генами, которые действуют суммирующе, эквивалентно. Гены эти называют полимерными и, поскольку они однозначно действуют на один и тот же признак, было принято обозначать их одной латинской буквой с указанием индекса для разных генов: А₁; А₂; А₃ и т.д.

Полимерия – это такой тип неаллельного взаимодействия генов, когда разные локусы (гены) производят одинаковый или сходный фенотипический эффект.

При накоплении в фенотипе доминантных полимерных генов их действие суммируется. Эти гены имеют кумулятивный (аддитивный) эффект, поэтому взаимодействие такого типа называют кумулятивной полимерией. По такому типу наследуются в основном все количественные признаки: высота растения, длина колоса, метелки или початка, урожайность, содержание белка или жира.

При кумулятивной полимерии степень выражения количественного признака зависит от числа доминантных генов.

Изучая наследование перечисленных признаков, можно заметить, что F₁ характеризуется промежуточным фенотипом, а в F₂ образуется непрерывный вариационный ряд по внешнему проявлению данного признака, то есть нельзя выделить четких фенотипических классов, как при наследовании альтернативных признаков (красная или белая окраска цветка, гладкие или морщинистые формы семян у гороха).

Изменчивость количественного признака в отличие от альтернативного оценивается амплитудой его варьирования.

Шведский генетик Нильсон-Эле, скрещивая разные линии пшеницы с красными и белыми зернами, установил, что гибридные семена были промежуточными по окраске, а в F₂ обнаружил расщепление в соотношении 3 : 1; 15 : 1; 63 : 1, т. е. окраска зерна определяется одной, двумя или тремя парами полигенов. Генотипы линий пшеницы можно обозначить как АА и аа; А₁А₁А₂А₂ и а₁а₁а₂а₂; А₁А₁А₂А₂А₃А₃ и а₁а₁а₂а₂а₃а₃. При увеличении числа пар генов, ответственных за признак, снижается частота фенотипов с крайними проявлениями признака. Это можно рассчитать, используя формулу 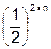, где n – число пар генов.

При моногенном признаке частота крайних фенотипов (гомозигот) составляет: 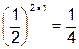; при дигенном признаке - 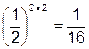, при полигенном признаке - .

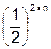Если скрещиваются две родительские формы, обладающие в равной степени каким-нибудь желательным признаком, то в результате расщепления в потомстве могут образовываться формы, превосходящие обоих родителей по этому признаку.

Явление выщепления в потомстве гибридов особей с более сильным или слабым проявлением количественных признаков называется трансгрессией. Это захождение признаков у гибридов за признаки родителей может быть положительным или отрицательным. Явление трансгрессии характерно для кумулятивной полимерии.

В основе образования трансгрессий лежит процесс, который проще всего можно пояснить при помощи следующей схемы:

РР ?А₁А₁а₂а₂ × ? а₁а₁А₂А₂

F₁ А₁а₁А₂а₂

F₂ А₁А₁А₂А₂ …………а₁а₁а₂а₂

(положительная (отрицательная

трансгрессия) трансгрессия)

В этой схеме каждая родительская форма несет один доминантный ген (соответственно А₁ и А₂), связанный с определенным признаком. В потомстве F₁ (А₁а₁А₂а₂) могут возникнуть комбинации, которые являются трансгрессивными, то есть превосходят родителей по степени развития данного признака. Одна из таких комбинаций А₁А₁А₂А₂ содержит оба доминантных гена и представляет собой положительную трансгрессию; напротив, комбинация а₁а₁а₂а₂ представляет собой отрицательную трансгрессию, утратившую как ген А₁, так и ген А₂. Частота трансгрессивных форм зависит от числа полигенов, контролирующих признак: чем больше генов – тем меньше трансгрессивных форм. Полимерные гены с однозначным действием могут наследственно определять и качественные признаки. Примером такого действия полигенов может служить наследование формы плода (стручка) у пастушьей сумки. У этого вида обычно встречаются растения с треугольной и очень редко – с яйцевидной формой плода. От скрещивания этих форм между собой в F₁ появляются растения, плоды у которых треугольной формы, а в F₂ наблюдается расщепление в отношении 15 : 1.

При тригибридном скрещивании расщепление по таким генам будет 63 : 1. Такого рода доминантные однозначные гены называют генами некумулятивного действия, а явление подобного взаимодействия – некумулятивной полимерией.

В случае некумулятивной полимерии наличие в генотипе разного количества доминантных полимерных генов однозначного действия не изменяет выраженности признака. Достаточно одной доминантной аллели любого из генов, чтобы вызвать развитие признака.

Для изучения изменчивости количественных признаков применяют статистический метод. Предмет измерения (вес, рост, длина, высота и т.д.) обычно обозначают символом х, а его среднюю величину – как 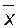(читается: икс с черточкой). Точно так же вместо того, чтобы писать «сумма всех показателей веса или длины» статистики пользуются греческой буквой сигма ( 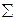). Средняя величина признака определяется по формуле 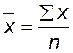, где n – число особей.

Среднее значение признака дает представление, например, о весе отдельных пород кроликов, высоте растений различных сортов или познаниях наших студентов. Средняя арифметическая величина представляет собой как бы точку равновесия вариационного ряда, отклонения от которой в сторону увеличения или уменьшения признака взаимно уравновешивается. Средняя арифметическая показывает, какую величину признака имели бы растения данного сорта, если бы она была у всех одинаковой.

Средняя арифметическая не может служить показателем изменчивости вариационного ряда, так как характеризует лишь среднюю величину признака особей данной группы.

Лучшим показателем было бы среднее отклонение, определяемое путем перемножения величин отклонения от средней каждого класса и его частоты, суммирования всех произведений и деления полученной цифры на число особей (n). Но практически средним отклонением редко пользуются. Биологи предпочитают пользоваться стандартным отклонением, обозначаемым малой греческой буквой сигма ( 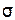). Его определяют путем возведения в квадрат отклонения от средней каждого класса и умножения произведения на частоту данного класса, сложения всех произведений и деления их суммы на n (или на n-1), а затем извлечения корня квадратного из полученного частного. Если частоты разных классов обозначить как f, а отклонения этих классов – от средней как d, то получим следующую формулу вычисления стандартного отклонения: 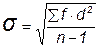. Выражение (n-1) в теории вероятностей называют числом степеней свободы.

Среднее квадратическое отклонение служит мерилом изменчивости вариационного ряда и связано с распределением в нем вариант. Определение стандартного отклонения необходимо для вычисления средней ошибки.

Математики определили, что при симметричном распределении популяций в нормальной кривой 68,3% особей укладываются на отрезке одного стандартного отклонения (1 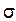) в большую и меньшую сторону от средней, 95,5% популяций уложатся в пределах двух стандартных отклонений (2 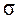) по обе стороны от средней, 99,7% - в пределах трех стандартных отклонений (3 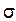), а 99,97% особей – в пределах 3,5 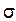. Практики же считают, что все особи вариационного ряда не выходят за пределы 3 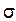по обе стороны от средней (правило «трех сигм»).

Среднее квадратическое отклонение – число именованное, оно не может быть использовано при сравнении изменчивости разных признаков. Для этой цели вводится коэффициент вариации, представляющий собой среднее квадратическое отклонение, выраженное в процентах от средней арифметической, то есть 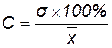. Так, путем сравнения величин сигм нельзя определить, какой признак в изучаемом сорте, например, подсолнечника, более изменчив – число семянок в корзинке или содержание жира в них. Лишь рассчитав коэффициенты вариации для этих признаков, можно сказать, что изменчивость числа семянок в корзинке выше или ниже, чем изменчивость содержания жира в них.

Оценивая популяцию сорта на основе данных о среднем и стандартном отклонении у определенной выборки особей, следует убедиться в надежности (достоверности) вычисленной средней. Хорошим показателем достоверности средней служит ее средняя ошибка, которая зависит от числа измерений (выборки) и величины изменчивости данной популяции. Средняя ошибка вычисляется по следующей формуле: 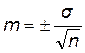. Ошибка средней обычно записывается рядом со средним значением признака: .

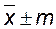Для решения вопроса о существенности разницы между средними арифметическими определяют критерий достоверности: 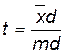, т. е. отношение отклонения разницы к ошибке.

Таким образом, фенотипическую изменчивость количественных признаков определяют по таким статистическим параметрам как 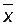, , 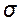С. Для генетического анализа изменчивости количественных признаков требуется разложить фенотипическую изменчивость, выраженную через вариансу ( 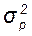), на составляющие варианты: генотипическую ( 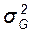), и паратипическую ( 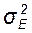). Это позволяет установить долю изменчивости в группе особей, обусловленную их генетическим разнообразием и долю изменчивости, связанную с влиянием факторов среды (средовую).

Задачи 

1. От скрещивания двух линий пастушьей сумки, характеризующихся одна треугольными, другая – яйцевидными стручками, возникли треугольноплодные гибриды. Во втором поколении было получено 195 треугольноплодных и 12 яйцевидноплодных растений. Определите:

а) тип полимерного взаимодействия генов;

б) генотипы и фенотипы родителей и всех форм F₂.

2. При скрещивании двух растений было обнаружено, что 63/64 всего потомства подобно либо одному, либо другому родителю, а 1/64 часть потомства отличается от обоих родителей. Все растения второго типа похожи друг на друга. Каково генетическое объяснение этого результата?

3. У пшеницы яровость контролируется двумя доминантными полимерными генами, а озимость – их рецессивными аллелями. В каком соотношении будет идти расщепление по фенотипу во втором поколении от скрещивания двух яровых сортов пшеницы, имеющих генотипы А₁А₁а₂а₂ и а₁а₁А₂А₂?

4. У одной линии кукурузы в початке имеется 16 рядов зерен, а у другой линии – 8 рядов. У F₁, полученного от скрещивания этих линий, наблюдается промежуточный фенотип, в среднем 12 рядов. Второе поколение фенотипически неоднородно, количество рядов варьирует от 8 до 16, причем примерно в двух из каждых 16 початков имеется столько же рядов зерен, сколько у Р₁ и Р₂. Сколько генов определяют данный признак?

5. От скрещивания двух линий кукурузы, характеризующихся двенадцатирядными початками, возникли гибриды тоже с двенадцатирядными початками. Во втором поколении получено растений: 802 с 12-рядными початками, 540 с десятирядными, 525 с 14-рядными, 142 с 8-рядными и 123 с 16-рядными. Проанализируйте данное расщепление с помощью решетки Пеннета. Постройте кривую распределения частот генотипов в F₂.

6. Высокорослый сорт скрестили с низкорослым. В первом поколении возникли гибриды с промежуточным ростом, а во втором – среди 523 растений обнаружено 2 таких же высоких, как мать, и 3 таких же низких, как отец. Определите:

а) число локусов, контролирующих высоту растения;

б) генотипы родителей.

7. Если различия в проявлении какого-либо количественного признака обусловлены только пятью парами аллелей, действие которых кумулятивно, то при скрещивании двух крайних по проявлению этого признака типов какова будет в F₂ доля особей каждого из этих крайних типов?

8. В результате изучения опушенности стебля сои была обнаружена сильная изменчивость этого признака (от 60 волосков на 1 см² до полного их отсутствия). Допустим, что эта изменчивость обусловлена тремя парами генов с кумулятивным действием.

При скрещивании сорта сои с максимальной опушенностью стебля (60 волосков на 1 см²) с сортом, совершенно не имеющим опушения на стебле (0 волосков), у всех растений F₁ наблюдается промежуточная опушенность (30 волосков на 1 см²). Растения F₁ были подвергнуты самоопылению; в F₂ провели оценку на опушенность;

а) определите генотипы родительских форм и F₁;

б) какова ожидаемая доля в F₂ растений с максимальной и промежуточной опушенностью?

в) какая часть растений F₂ будет иметь 40 волосков на 1 см²?

г) какая часть потомства F₂ будет гомозиготной по генам, обусловливающим данный признак?

9. Допустим, что цвет кожи у человека определяется взаимодействием двух полимерных генов, то есть цвет кожи тем темнее, чем больше доминантных генов в генотипе. Потомка темнокожего и белого называют мулатом. Если темнокожий и белая женщина имеют детей, то:

а) в какой пропорции можно ожидать появления детей полных  мулатов, белых?

б) могут ли два светлокожих иметь детей более темных, чем они сами? Или более светлых? Почему?

10. Если два мулата (А₁а₁А₂а₂) имеют детей, то можно ли ожидать среди них полных? Белых? Мулатов? Какую долю составят дети каждого типа?

11. Овцы одной породы имеют длину шерсти 40 см, а другой – 10 см. Предположим, что различия между породами зависят от трех пар генов с однозначным действием. Каковы будут F₁ и F₂?