Сечениями на действие изгибающих моментов

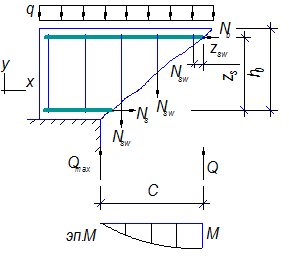
Рисунок 9.5 – Схема усилий в наклонном сечении при расчёте его на действие изгибающего момента

Рассмотрим равновесие элемента (рис. 9.5) и составим уравнение моментов действующих усилий относительно точки приложения равнодействующей напряжений в сжатом бетоне .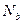

, (**)

,

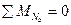
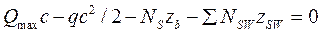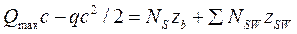где 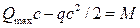- момент в наклонном сечении с длиной проекции 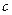на продольную ось элемента от внешней нагрузки;

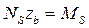- момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение;

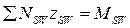- момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение.

Подставив М, М_S, M_SW в исходное уравнение (**) получим условие прочности изгибаемого элемента по наклонному сечению на действие изгибающего момента

.

;

.

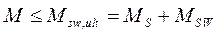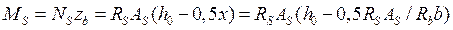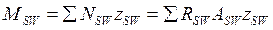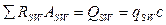- проинтегрируем данное выражение по переменной .

,

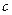где 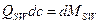, тогда .

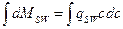Интегрируя, получим ,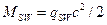

где ,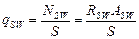

Величину 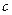принимают из условия, что поперечная сила в наклонном сечении воспринимается только поперечными стержнями, т.е. 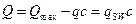, отсюда выразим .

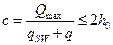При действии на элемент сосредоточенных сил значение 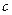принимают равным расстояниям от опоры до точек приложения этих сил, а так же равным 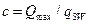, но не меньше 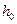, если это значение меньше расстояния от опоры до 1-го груза.

Расчёт на действие момента производят для наклонных сечений, расположенных:

- у грани крайней свободной опоры элементов;

- в местах обрыва продольной арматуры в пролёте;

- в местах резкого изменения высоты элемента;

- у свободного края консолей.

Несущая способность наклонного сечения по изгибающему моменту не должна быть ниже несущей способности нормального сечения, проходящего через эту точку. При достаточной анкеровке продольной рабочей арматуры на крайних опорах и в пролётах это требование будет выполняться, и тогда расчёт наклонных сечений по изгибающему моменту можно не производить:

1. При отсутствии наклонных трещин, т.е. при соблюдении условия 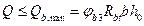, растянутые стержни должны быть заведены за внутреннею грань свободной опоры на длину анкеровки .

2. Если 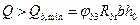, т.е. при наличии наклонных трещин, длина запуска арматуры за грань опоры должна быть 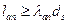и не менее 200 мм. Для стержней диаметром менее 36 мм значение коэффициента 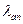= 15 – 93 принимают по таблице норм в зависимости от классов бетона и арматуры и коэффициента ά, учитывающего влияние поперечного обжатия бетона и поперечной арматуры.

3. Обрываемые в пролёте стержни должны заводиться за точку теоретического обрыва, т.е. за нормальное сечение, в котором внешний момент становится равным предельному моменту 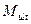без учёта обрываемой арматуры (рис. 23), на длину ,

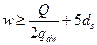где 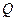- поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва.

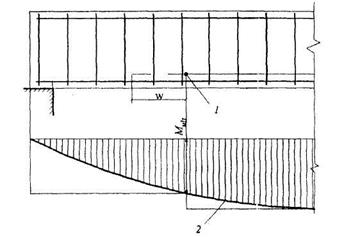
Рисунок 9.6 – Обрыв растянутых стержней в пролете

1- точка теоретического обрыва; 2- эпюра М