О характере работы и разрушения внецентренно сжатых элементов
Напряжённо-деформированное состояние внецентренно сжатых элемента зависит от его гибкости, величины эксцентриситета приложения сжимающей силы, длительности действия нагрузки, вида закрепления элемента и других факторов.
В зависимости от величины эксцентриситета различают два случая внецентренного сжатия:
- случай больших эксцентриситетов 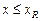 ;
; 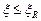 (рис. 11.1а),
(рис. 11.1а),
- случай малых эксцентриситетов 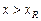 ;
; 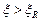 (рис. 11.1б).
(рис. 11.1б).
В случае больших эксцентриситетов разрушение элемента происходит по растянутой зоне, характер разрушения аналогичен разрушению изгибаемых элементов. Напряжения в растянутой арматуре становятся равными пределу текучести стали ( 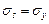 ) и затем при напряжениях в сжатом бетоне, равных расчётному сопротивлению бетона на осевое сжатие (призменной прочности)
) и затем при напряжениях в сжатом бетоне, равных расчётному сопротивлению бетона на осевое сжатие (призменной прочности) 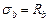 , а в сжатой арматуре напряжений, равных пределу текучести стали
, а в сжатой арматуре напряжений, равных пределу текучести стали 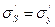 , происходит разрушение элемента.
, происходит разрушение элемента.
В случае малых эксцентриситетов разрушение элемента происходит по сжатой зоне вследствие исчерпания несущей способности бетона сжатой зоны и сжатой арматуры. Напряжения в бетоне становятся равными расчётному сопротивлению бетона на осевое сжатие (призменной прочности) 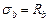 , а напряжения в сжатой арматуре становятся равными пределу текучести стали
, а напряжения в сжатой арматуре становятся равными пределу текучести стали  . Напряжения в растянутой или в менее сжатой арматуре (при полностью сжатом сечении) не достигают предела текучести стали
. Напряжения в растянутой или в менее сжатой арматуре (при полностью сжатом сечении) не достигают предела текучести стали  , т.е. прочностные свойства данной арматуры используются не полностью.
, т.е. прочностные свойства данной арматуры используются не полностью.
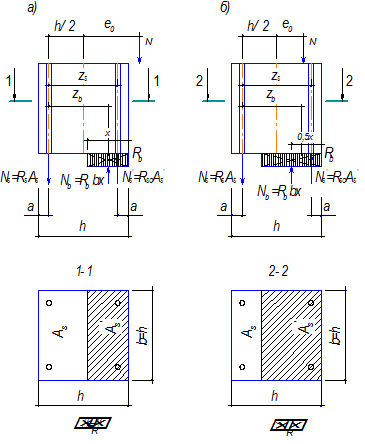
Рисунок 11.1 – Расчётные случаи внецентренно сжатых элементов:
а – случай больших эксцентриситетов; б – случай малых эксцентриситетов.
2. Учёт влияния прогиба элемента

Рисунок 11.2 – Учёт влияния продольного изгиба элемента
Под действием продольной сжимающей силы  , приложенной с эксцентриситетом
, приложенной с эксцентриситетом 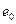 , гибкие сжатые элементы с гибкостью
, гибкие сжатые элементы с гибкостью 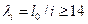 , а для прямоугольных сечений с гибкостью
, а для прямоугольных сечений с гибкостью 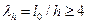 начинают изгибаться (рис. 2). Это вызывает перемещение верха колонны, вследствие чего продольная сила
начинают изгибаться (рис. 2). Это вызывает перемещение верха колонны, вследствие чего продольная сила  действует уже с большим эксцентриситетом
действует уже с большим эксцентриситетом 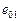 . Таким образом, снижается несущая способность элемента посредством увеличения изгибающего момента
. Таким образом, снижается несущая способность элемента посредством увеличения изгибающего момента 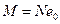 до величины
до величины 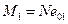 . Влияние изгиба на несущую способность сжатых элементов необходимо учитывать расчётом по деформированной схеме, принимая во внимание неупругие свойства бетона и арматуры и наличие трещин в элементе. Из-за сложности такого расчёта нормы допускают расчёт конструкции производить по недеформированной схеме, а расчёт влияния прогиба учитывать при помощи коэффициента η (
. Влияние изгиба на несущую способность сжатых элементов необходимо учитывать расчётом по деформированной схеме, принимая во внимание неупругие свойства бетона и арматуры и наличие трещин в элементе. Из-за сложности такого расчёта нормы допускают расчёт конструкции производить по недеформированной схеме, а расчёт влияния прогиба учитывать при помощи коэффициента η ( 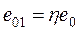 ), который определяют по формуле:
), который определяют по формуле:
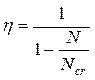 ,
,
где 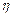 - принимает значения от 1,0 до 2,5;
- принимает значения от 1,0 до 2,5;
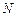 - усилие, действующее на элемент;
- усилие, действующее на элемент;
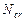 - условная критическая сила Эйлера
- условная критическая сила Эйлера 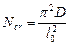 ,
,
где D – жесткость железобетонного элемента в предельной стадии равная:
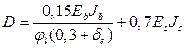 - для произвольного сечения и
- для произвольного сечения и
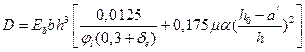 - для прямоугольного сечения.
- для прямоугольного сечения.
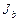 ,
, 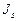 - момент инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;
- момент инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;
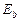 ,
, 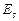 - модуль упругости бетона и арматуры;
- модуль упругости бетона и арматуры;
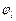 - коэффициент, учитывающий влияние длительного действия нагрузки
- коэффициент, учитывающий влияние длительного действия нагрузки 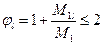 ,
,
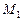 и
и 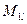 , - моменты внешних сил относительно оси, перпендикулярной плоскости изгиба и проходящей через центр наиболее растянутого или наименее сжатого (при полностью сжатом сечении) стержня арматуры, соответственно от действия всех нагрузок и от действия постоянных и длительных нагрузок. Допускается определять изгибающие моменты относительно оси проходящей через центр тяжести всей растянутой арматуры.
, - моменты внешних сил относительно оси, перпендикулярной плоскости изгиба и проходящей через центр наиболее растянутого или наименее сжатого (при полностью сжатом сечении) стержня арматуры, соответственно от действия всех нагрузок и от действия постоянных и длительных нагрузок. Допускается определять изгибающие моменты относительно оси проходящей через центр тяжести всей растянутой арматуры.
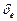 - относительный эксцентриситет
- относительный эксцентриситет 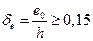 ,
,
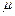 - коэффициент армирования
- коэффициент армирования 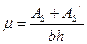 .
.
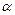 - коэффициент приведения площади арматуры к площади бетона
- коэффициент приведения площади арматуры к площади бетона 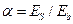 .
.
Если гибкость элемента 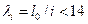 , а для прямоугольных сечений
, а для прямоугольных сечений 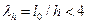 , то
, то 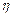 = 1,0. Если
= 1,0. Если 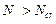 , то необходимо увеличить сечение элемента.
, то необходимо увеличить сечение элемента.
3. Расчёт сжатых элементов прямоугольного сечения в случае больших эксцентриситетов
Случай больших эксцентриситетов имеет место, если 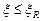 (рис 11.3а).
(рис 11.3а).
Предельные усилия, воспринимаемые бетоном и арматурой:
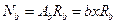 ;
; 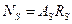 ;
; 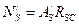 .
.
Плечи внутренних пар сил, согласно чертежа на рис. 11.3:
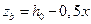 ;
; 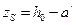 .
.
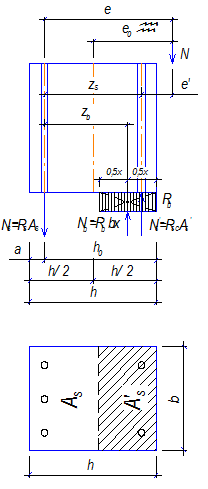
Рисунок 11.3 – Схема усилий при расчёте прочности
внецентренно сжатого элемента
Эксцентриситеты приложения сжимающей силы относительно центров тяжестей растянутой и сжатой арматур:
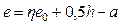 ;
; 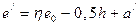 .
.
Рассмотрим равновесие элемента (рис. 11.3) под действием продольной сжимающей силы 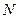 и внутренних усилий, возникающих в сжатых бетоне
и внутренних усилий, возникающих в сжатых бетоне 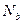 , в растянутой и сжатой арматуре
, в растянутой и сжатой арматуре 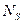 и
и 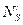 .
.
1.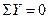 -сумма проекций, действующих сил на вертикальную ось.
-сумма проекций, действующих сил на вертикальную ось.
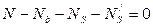 ;
;
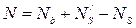 ;
; 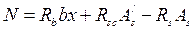 .
.
Выражение 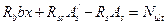 представляет собой предельное усилие, воспринимаемое данным сечением.
представляет собой предельное усилие, воспринимаемое данным сечением.
Тогда условие прочности внецентренно сжатого элемента в случае больших эксцентриситетов примет вид:
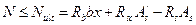
Приравняв внешнее и внутреннее усилия 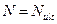 , определим площадь растянутой арматуры:
, определим площадь растянутой арматуры:
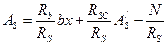 и, заменяя,
и, заменяя, 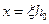 будем иметь
будем иметь
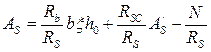 .
.
2.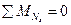 -сумма моментов, действующих сил относительно центра тяжести растянутой арматуры.
-сумма моментов, действующих сил относительно центра тяжести растянутой арматуры.
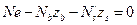 ;
;
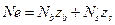 ;
; 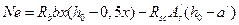 .
.
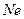 - момент сжимающей силы, который называют заменяющим моментом.
- момент сжимающей силы, который называют заменяющим моментом.
Выражение 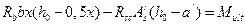 представляет собой предель- ный изгибающий момент, воспринимаемый данным сечением, т.е.
представляет собой предель- ный изгибающий момент, воспринимаемый данным сечением, т.е. 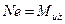 .
.
Предельный момент может достигнут за счёт увеличения либо сжимающей продольной силы 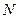 , либо эксцентриситета её приложения
, либо эксцентриситета её приложения 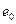 , либо того и другого вместе:
, либо того и другого вместе:
если 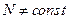 , а
, а 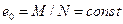 , то
, то 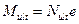 ;
;
если 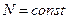 , а
, а 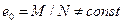 , то
, то 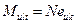 .
.
На практике чаще встречается случай когда 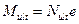 , его и рассмотрим.
, его и рассмотрим.
Тогда моментное условие прочности внецентренно сжатого элемента в случае больших эксцентриситетов примет вид:
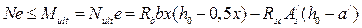 .
.
Выполним подстановку 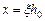 , тогда
, тогда
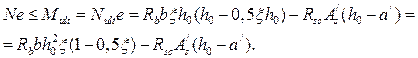
Обозначив 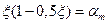 , получим условие прочности в следующем виде:
, получим условие прочности в следующем виде:
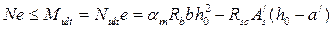 .
.
Приравняв внешний и внутренний моменты 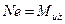 , выразим площадь сечения сжатой арматуры
, выразим площадь сечения сжатой арматуры 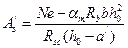
или коэффициент 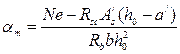 .
.
При симметричном армировании сечения, когда 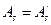 и
и 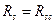 из силового условия прочности получим
из силового условия прочности получим 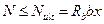 . Приравняв внешнее и внутреннее усилия
. Приравняв внешнее и внутреннее усилия 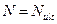 , выразим высоту сжатой зоны бетона
, выразим высоту сжатой зоны бетона 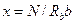 , значение которой подставим в моментное уравнение прочности. После алгебраических преобразований получим выражение для определения площадей сжатой и растянутой арматур:
, значение которой подставим в моментное уравнение прочности. После алгебраических преобразований получим выражение для определения площадей сжатой и растянутой арматур: 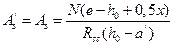 .
.
Условия применения вышеприведённых формул:
1. 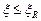 (
( 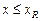 ,
, 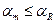 ) – в этом случае напряжения в растянутой арматуре достигают предельных значений.
) – в этом случае напряжения в растянутой арматуре достигают предельных значений.
2. 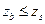 (
( 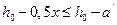 или
или 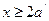 ) – в этом случае напряжения в сжатой арматуре достигают предельных значений.
) – в этом случае напряжения в сжатой арматуре достигают предельных значений.
4. Расчёт сжатых элементов прямоугольного сечения в случае малых эксцентриситетов
Случай 2 (малых эксцентриситетов), когда ξ >ξR
Этот случай имеет место при загружении элемента с малым эксцентриситетом продольной силы, либо при очень сильной арматуре Аs. Сечение может быть полностью сжато или сжата его большая часть, находящаяся ближе к продольной силе, а остальная часть сечения испытывает относительно слабое растяжение. Разрушается такой элемент вследствие исчерпания прочности в бетоне и арматуре в части сечения, расположенной ближе к продольной силе при соблюдении условия ξ >ξR. При этом напряжения (сжимающие или растягивающие) в части сечения, более удаленной от сжимающей силы, остаются сравнительно низкими, и прочность материалов (в первую очередь арматуры Аs) там недоиспользуется.
Рассмотрим расчёт внецентренно сжатого элемента прямоугольного сечения при бетоне класса не выше ВЗО и арматуре класса A400 и ниже, расчётная схема которого представлена на рис. 11.4.
Расчёт несущей способности, как и для случая 1, производится из условия

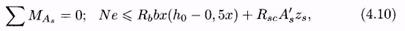
где е = е0 + 0,5h -а.
При этом высота сжатой зоны сечения определяется из совместного решения уравнения 
 и линейной зависимости
и линейной зависимости

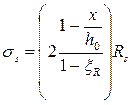
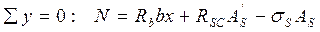

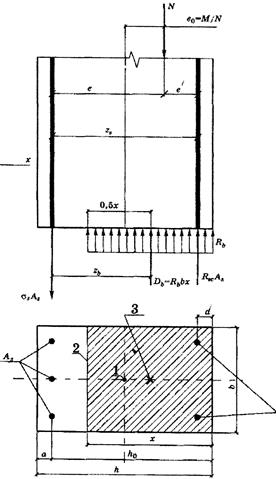
Рисунок 11.4 – Расчетная схема внецентренно сжатого элемента прямоугольного поперечного сечения, работающего по случаю 2: 1 – геометрическая ось элемента; 2 – граница сжатой зоны; 3 – центр тяжести площади бетона сжатой зоны
Расчёт несущей способности, как и для случая 1, производится из условия
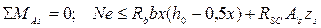
где е = е0 + 0,5h -а. При этом высота сжатой зоны сечения определяется из совместного решения уравнения 

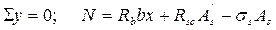
и линейной зависимости
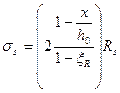
При любых сечениях, внешних усилиях, любом армировании и классе бетона рекомендуется пользоваться формулами общего случая расчёта [2, п. 3.28].
Из плоскости изгиба внецентренно сжатый элемент рассчитывается также как внецентренно сжатый с эксцентриситетом, равным случайному.
Дата добавления: 2014-12-30; просмотров: 2468;
