С полкой в сжатой зоне
При расчётеизгибаемых элементов таврового сечения с полкой в сжатой зоне в зависимости от положения нейтральной оси возможны два случая расчёта:
- нейтральная ось находится в пределах полки 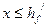 (1 случай);
(1 случай);
- нейтральная ось находится в пределах ребра 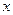 >
> 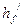 (2 случай).
(2 случай).
1) Определение случая расчёта
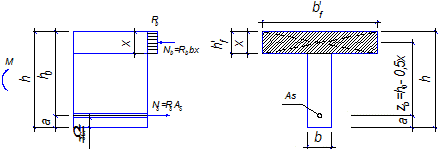
Рисунок 8.4 – Схема усилий при определении случая расчёта
изгибаемых элементов таврового сечения
Предположим, что нейтральная ось проходит по низу полки, т.е. вся полка сжата и тогда 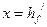 .
.
Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре равны:
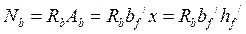 ,
, 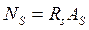 .
.
Плечо внутренней пары сил 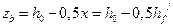 .
.
Рассмотрим равновесие элемента (рис. 15) под действием изгибающего момента от нагрузки 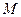 и внутренних усилий, возникающих в сжатом бетоне
и внутренних усилий, возникающих в сжатом бетоне 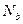 и растянутой арматуре
и растянутой арматуре 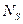 .
.
1. 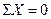 ;
;
 ;
; 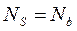 ;
; 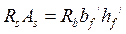 .
.
Если 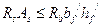 , то
, то 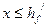 , т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.
, т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.
Если 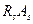 >
> 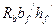 , то
, то 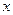 >
> 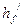 , т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений.
, т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений.
Данные уравнения применяют для определения случай расчёта тавровых сечений при решении I типа задач – проверки прочности, заданного сечения элемента.
2.  ;
;
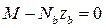 ;
; 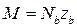 ;
; 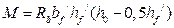 .
.
Выражение 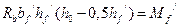 представляет собой изгибающий момент, воспринимаемый сжатой полкой.
представляет собой изгибающий момент, воспринимаемый сжатой полкой.
Если 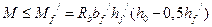 , то
, то 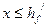 , т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.
, т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.
Если 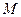 >
> 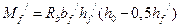 , то
, то 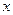 >
> 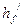 , т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений.
, т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений.
Данные уравнения применяют для определения случай расчёта тавровых сечений при решении II типа задач – расчёта сечений элемента.
2) Расчёт прочности изгибаемых элементов таврового
сечения по I случаю расчёта
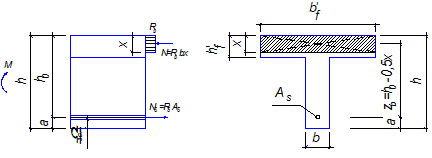
Рисунок 8.5 – Схема усилий по I случаю расчёта прочности
изгибаемых элементов таврового сечения
Предположим, что выполняются следующие условия:
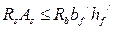 и
и
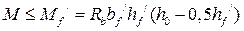 ,
,
тогда 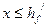 нейтральная ось находится в пределах полки, и имеем I случай расчёта.
нейтральная ось находится в пределах полки, и имеем I случай расчёта.
Так как растянутый бетон в расчёте не учитывают, по причине наличия в нём трещин, то расчёт прочности тавровых сечений со сжатой зоной в пределах полки выполняют аналогично расчёту прямоугольных сечений с размерами 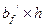 . В расчётных формулах вместо ширины сечения
. В расчётных формулах вместо ширины сечения 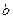 подставляют ширину полки
подставляют ширину полки 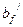 (кроме формулы для определения минимальной площади арматуры):
(кроме формулы для определения минимальной площади арматуры):

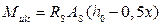
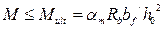
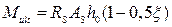

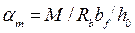
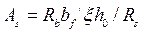
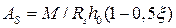
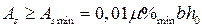
3) Расчёт прочности изгибаемых элементов таврового
сечения по II случаю расчёта
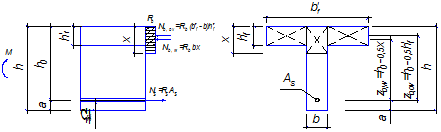
Рисунок 8.6 – Схема усилий по II случаю расчёта прочности
изгибаемых элементов таврового сечения
Предположим, что выполняются следующие условия:
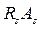 >
> 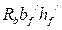 и
и
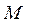 >
> 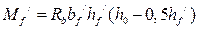 ,
,
тогда 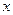 >
> 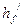 нейтральная ось находится в пределах ребра, и имеем II случай расчёта.
нейтральная ось находится в пределах ребра, и имеем II случай расчёта.
Условно разделим площадь сжатой зоны бетона 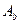 на две части: площадь бетона сжатого ребра
на две части: площадь бетона сжатого ребра 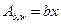 и площадь бетона сжатых свесов
и площадь бетона сжатых свесов 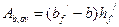 .
.
Предельное усилие, воспринимаемое сжатым бетоном 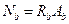 , определим как сумму усилий, которые воспринимают сжатый бетон ребра
, определим как сумму усилий, которые воспринимают сжатый бетон ребра 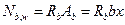 и сжатый бетон свесов
и сжатый бетон свесов 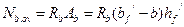 .
.
Плечи пар сил (расстояния от центра тяжести сечения арматуры до точек приложения каждого из усилий) в соответствие с рис. 8.6 равны  и
и 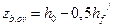
Рассмотрим равновесие элемента (рис. 16) под действием изгибающего момента от нагрузки М и внутренних усилий, возникающих в сжатом бетоне 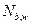 и
и  , и растянутой арматуре
, и растянутой арматуре  .
.
1. 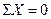 ;
;
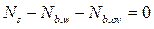 ;
; 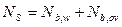 ;
;
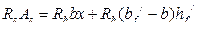 .
.
Высота сжатой зоны бетона ребра равна
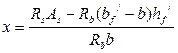 .
.
Площадь сечения растянутой арматуры
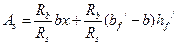 , подставив в формулу
, подставив в формулу 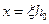 , получим
, получим
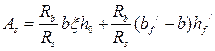 .
.
2. 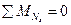 ;
;
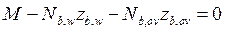 ;
; 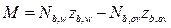 ;
;
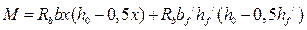 .
.
Выражение 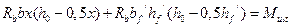 представляет собой предельный изгибающий момент, воспринимаемый данным сечением, который называют несущей способность сечения.
представляет собой предельный изгибающий момент, воспринимаемый данным сечением, который называют несущей способность сечения.
Тогда условие прочности изгибаемого элемента таврового сечения на действие изгибающего момента примет вид
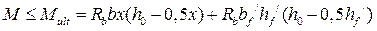 .
.
Выполнив подстановку 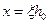 , получим
, получим
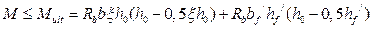 =
=
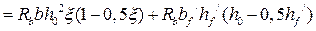 .
.
Обозначив 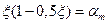 , получим условие прочности изгибаемого элемента таврового сечения в другом виде
, получим условие прочности изгибаемого элемента таврового сечения в другом виде
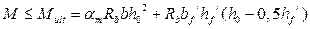 .
.
Приравняв внешний и внутренний моменты 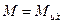 , можно определить коэффициенты
, можно определить коэффициенты
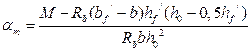 и
и
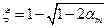 .
.
Приведённые выше формулы справедливы при условии 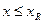 или
или 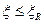 , т.е. когда разрушение элемента происходит по растянутой зоне.
, т.е. когда разрушение элемента происходит по растянутой зоне.
Если разрушение элемента происходит по сжатой зоне, т.е. 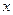 >
> 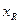 или
или 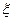 >
> 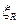 , то максимальный предельный изгибающий момент, воспринимаемый тавровым сечением, определяют исходя из значения граничной высоты сжатой зоны бетона
, то максимальный предельный изгибающий момент, воспринимаемый тавровым сечением, определяют исходя из значения граничной высоты сжатой зоны бетона 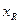 , которой соответствуют величины
, которой соответствуют величины 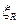 ,
, 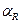 ,
, 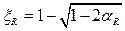 , тогда
, тогда
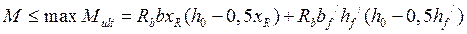 и
и
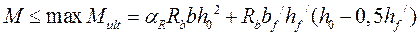 .
.
Дата добавления: 2014-12-30; просмотров: 1720;
