Минимизация не полностью определенных ПФ
ПФ называется не полностью определенной или частично определенной, если число наборов n аргументов, на которых ее значение задано, меньше 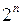 . С точки зрения практической реализации такой ПФ это может означать, что наборы аргументов, на которых значение функции не определено, никогда не появляются на входах КС либо формируемые на таких наборах выходные сигналы являются несущественными.
. С точки зрения практической реализации такой ПФ это может означать, что наборы аргументов, на которых значение функции не определено, никогда не появляются на входах КС либо формируемые на таких наборах выходные сигналы являются несущественными.
Из этого следует, что на таких наборах аргументов функция может быть произвольно доопределена значениями 0 или 1. Обычно доопределение производят, исходя из соображений минимизации. Рассмотрим ПФ, заданную картой Карно (табл. 4.17).
Таблица 4.17

| x2 | |||
 x1 x1
| - | |||
| - | ||||

| x3 |
Значения этой функции определены на шести наборах. Если функцию не доопределять, то минимальная ДНФ запишется в следующем виде:
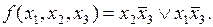
Доопределим заданную функцию единицами на оставшихся двух наборах (табл. 4.18).
Таблица 4.18

| x2 | |||
    x1 x1
| ||||

| x3 |
Тогда минимальную ДНФ можно записать в более простом виде:
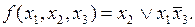
В некоторых случаях для получения минимальной ДНФ выгодно на некоторых наборах доопределить функцию единицами, а на остальных наборах – нулями или оставить неопределенной. Пусть функция задана картой Карно (табл. 4.19). Доопределим ее единицами сначала на всех неопределенных наборах (табл. 4.20), а затем только на одном из них (табл. 4.21), и запишем для каждой карты Карно получающиеся минимальные ДНФ.
Таблица 4.19

| x2 | |||
   x1 x1
| - | |||
| - | ||||

| x3 |
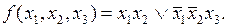
Таблица 4.20

| x2 | |||
     x1 x1
| ||||

| x3 |
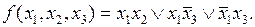
Таблица 4.21

| x2 | |||
   x1 x1
| - | |||

| x3 |
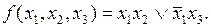
Частичное доопределение не полностью определенной ПФ требует перебора большого числа возможных вариантов и может дать ощутимую выгоду при минимизации на картах Карно для функций небольшого числа аргументов.
Для применения других методов минимизации (например, метод Квайна – Мак-Класки) удобно доопределить функцию на всех неопределенных наборах (единицами или нулями) и выполнить следующие шаги:
1) любым способом найти сокращенную ДНФ (КНФ);
2) по импликантной матрице Квайна определить минимальную совокупность простых импликант, накрывающую только те конституенты 1 (конституенты 0), которые соответствуют наборам, на которых функция была изначально определена.
Дата добавления: 2014-12-27; просмотров: 1199;
