Минимизация ПФ методом Квайна
Идея минимизации ПФ методом Квайна заключается в применении двух соотношений:
1) 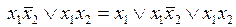 – соотношение (неполного) склеивания;
– соотношение (неполного) склеивания;
2) 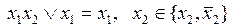 – соотношение поглощения.
– соотношение поглощения.
Справедливость этих соотношений можно проверить при помощи элементарных преобразований или по таблицам истинности.
Теорема Квайна. Если в совершенной дизъюнктивной нормальной форме ПФ провести все операции неполного склеивания и затем все операции поглощения, то в результате получится сокращенная ДНФ исходной ПФ, т.е. дизъюнкция всех ее простых импликант.
Доказательство этой теоремы приводится, например, в [7], при этом используется операция развертывания, обратная операции склеивания:
 .
.
Из формулировки теоремы Квайна следует, что в качестве исходной формы представления ПФ должна использоваться СДНФ. Если функция задана в произвольной форме, то вначале ее следует преобразовать к СДНФ. При этом переход от произвольной ДНФ к СДНФ осуществляется путем применения операции развертывания.
Практическое применение метода Квайна можно условно разделить на два этапа. На первом этапе минимизации производятся все возможные склеивания и поглощения по заданной СДНФ минимизируемой функции. В результате получается сокращенная ДНФ.
На втором этапе для получения минимальной ДНФ необходимо исключить из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью так называемой импликантной матрицы Квайна, которая представляет собой таблицу, столбцы которой отмечаются простыми импликантами, т.е. дизъюнктивными членами полученной на предыдущем этапе сокращенной ДНФ, а строки – членами СДНФ минимизируемой ПФ. При этом в ячейке импликантной матрицы на пересечении i-й строки и j-го столбца ставится отметка, если соответствующая этому столбцу импликанта является частью члена СДНФ, которому соответствует j-я строка.
Минимальная ДНФ строится по импликантной матрице следующим образом. Анализируются все возможные совокупности простых импликант (столбцы матрицы), накрывающие все члены СДНФ (строки матрицы). Простая импликанта накрывает член СДНФ, если на пересечении соответствующей строки и столбца матрицы имеется отметка. Одна импликанта может накрывать несколько строк. Из этих совокупностей выбирается одна (или несколько) с наименьшим числом членов (простых импликант), которая определяет минимальную ДНФ.
Для сокращения перебора можно пользоваться следующим подходом. Вначале по возможности определяются строки импликантной матрицы, в которых имеется только одна отметка. Простые импликанты, которым соответствуют эти отметки, называются базисными и обязательно входят в минимальную ДНФ функции, так как только эти простые импликанты в минимальной ДНФ представляют члены исходной СДНФ, записанные в найденных строках. Остальные строки импликантной матрицы должны быть накрыты минимальным числом простых импликант. В некоторых случаях базисные импликанты могут накрывать все строки.
Рассмотрим пример.
Пусть ПФ задана картой Карно (табл. 4.6). Ее СДНФ имеет вид
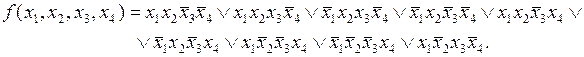
На первом этапе выполним все склеивания конституент 1 по одной переменной. При этом будет получена совокупность элементарных произведений, являющихся импликантами и представляющих собой общие части склеиваемых конституент. Для удобства присвоим каждому получаемому элементарному произведению порядковый номер. Не участвовавшие в очередном склеивании конституенты 1 или импликанты должны входить в последующие совокупности импликант в неизмененном виде.
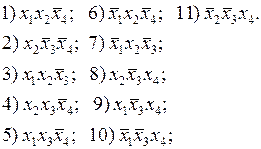
Повторим процедуру склеивания по одной переменной над каждой парой элементов совокупности импликант, полученных на предыдущем шаге. Будем повторять эту процедуру до тех пор, пока остаются элементарные произведения, между которыми возможно склеивание. Каждому элементу новой совокупности поставим в соответствие индекс, составленный из индексов импликант, участвующих в склеивании.
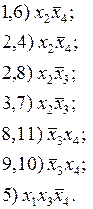
Полученную совокупность необходимо дополнить определенной на предыдущем этапе импликантой с порядковым номером 5, так как эта импликанта не участвовала в последующем склеивании (является простой).
Над полученной совокупностью элементарных произведений необходимо выполнить процедуру поглощения. В рассматриваемом примере совокупность элементарных произведений не содержит элементов, способных поглощать другие элементы, за исключением повторяющихся.
Окончательно, после исключения повторяющихся элементов, совокупность импликант запишется в следующем виде:
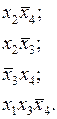
Дальнейшее выполнение склеиваний и поглощений невозможно.
Запишем сокращенную ДНФ минимизируемой функции:
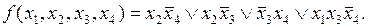
Построим импликантную матрицу Квайна (табл. 4.9).
Таблица 4.9
| № | Конституенты 1 | Простые импликанты | |||
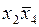
| 
| 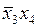
| 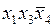
| ||
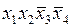
| + | + | |||
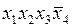
| + | + | |||
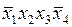
| + | ||||
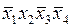
| + | + | |||
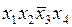
| + | + | |||
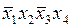
| + | + | |||
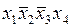
| + | ||||
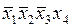
| + | ||||
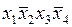
| + |
Поставим отметки в ячейках импликантной матрицы, находящихся на пересечении таких строк и столбцов, в которых простая импликанта является частью соответствующей конституенты 1.
Отыщем минимальное покрытие столбцами всех строк таблицы. Столбец импликантной матрицы, которому соответствует простая импликанта 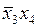 , обязательно должен войти в минимальное покрытие, поскольку только эта импликанта накрывает строки 7 и 8 матрицы.
, обязательно должен войти в минимальное покрытие, поскольку только эта импликанта накрывает строки 7 и 8 матрицы.
Кроме того, простая импликанта 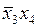 может представлять в минимальной совокупности еще две конституенты 1, находящиеся в строках 5 и 6.
может представлять в минимальной совокупности еще две конституенты 1, находящиеся в строках 5 и 6.
Аналогичные рассуждения можно провести в отношении простой импликанты 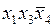 , поскольку только она может представлять в минимальной совокупности простых импликант строку 9 импликантной матрицы. Отметим, что эта импликанта также накрывает конституенту 1, записанную в строке 2.
, поскольку только она может представлять в минимальной совокупности простых импликант строку 9 импликантной матрицы. Отметим, что эта импликанта также накрывает конституенту 1, записанную в строке 2.
Таким образом, задача упростилась и заключается в нахождении минимального покрытия оставшихся трех конституент 1 (строки 1, 3, 4) оставшимися простыми импликантами.
Очевидно, что простая импликанта 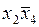 накрывает оставшиеся три строки матрицы. Следовательно, простая импликанта
накрывает оставшиеся три строки матрицы. Следовательно, простая импликанта  оказалась лишней и в минимальную ДНФ не входит.
оказалась лишней и в минимальную ДНФ не входит.
Окончательно минимальная ДНФ запишется в виде
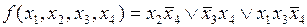 .
.
Метод Квайна является базовым методом минимизации ПФ.
4.3. Минимизация методом Квайна – Мак-Класки
Метод Квайна – Мак-Класки отличается от метода Квайна большей формализацией. Это достигается путем использования кубического представления ПФ (см. п. 3.6 учебного пособия) и сокращения перебора при выполнении операции склеивания. С учетом большей формализации метод Квайна – Мак-Класки удобно использовать при машинной реализации алгоритмов минимизации ПФ. Рассмотрим основные этапы этого метода.
На первом этапе необходимо представить ПФ в виде кубического комплекса 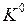 , представляющего собой совокупность 0-кубов, на которых минимизируемая ПФ принимает значение 1. Для этого в СДНФ функции каждый дизъюнктивный член заменяется n-разрядной двоичной комбинацией (n – число аргументов функции), представляющей собой номер конституенты 1, соответствующей этому дизъюнктивному члену. Иными словами, записываются n-разрядные двоичные наборы, на которых значение функции равно 1.
, представляющего собой совокупность 0-кубов, на которых минимизируемая ПФ принимает значение 1. Для этого в СДНФ функции каждый дизъюнктивный член заменяется n-разрядной двоичной комбинацией (n – число аргументов функции), представляющей собой номер конституенты 1, соответствующей этому дизъюнктивному члену. Иными словами, записываются n-разрядные двоичные наборы, на которых значение функции равно 1.
Далее все 0-кубы полученного кубического комплекса разбиваются на группы по числу единиц, входящих в их запись. Таким образом, максимальное число групп не превышает 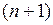 .
.
Производится склеивание 0-кубов, которое возможно только между соседними группами. Результаты склеивания составляют новый кубический комплекс 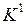 . Если часть 0-кубов не участвовала в склеивании, то такие 0-кубы являются простыми импликантами.
. Если часть 0-кубов не участвовала в склеивании, то такие 0-кубы являются простыми импликантами.
Формирование кубических комплексов продолжается до тех пор, пока не будет получен комплекс 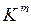 , не содержащий m-кубов, отличающихся только по одной координате. При этом сохраняется разбиение на группы по количеству единиц. Если на каком-либо этапе часть i-кубов не участвовала в склеивании, то такие i-кубы являются простыми импликантами и входят в минимальную ДНФ.
, не содержащий m-кубов, отличающихся только по одной координате. При этом сохраняется разбиение на группы по количеству единиц. Если на каком-либо этапе часть i-кубов не участвовала в склеивании, то такие i-кубы являются простыми импликантами и входят в минимальную ДНФ.
Рассмотрим пример.
Пусть подлежащая минимизации ПФ задана картой Карно (табл. 4.10).
Таблица 4.10

| x2 | ||||
    x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Заранее отметим на ней возможные простые импликанты для проверки правильности решения примера.
Для рассматриваемой функции СДНФ запишется в следующем виде:
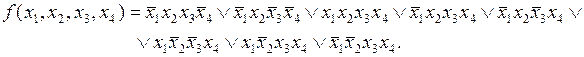
По СДНФ функции сформируем кубический комплекс 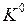 , каждый элемент которого представляет собой четырехразрядный двоичный набор. Если переменная
, каждый элемент которого представляет собой четырехразрядный двоичный набор. Если переменная 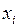 входит в запись конституенты 1 без инверсии, то i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 1. В противном случае i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 0.
входит в запись конституенты 1 без инверсии, то i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 1. В противном случае i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 0.
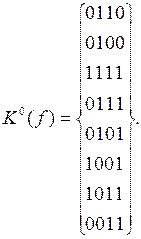
Сведем в таблицу (табл. 4.11) полученные 0-кубы, упорядоченные по числу единиц.
Таблица 4.11
| Кол-во единиц | 0-кубы |
| – | |
| 0110, 0101, 1001, 0011 | |
| 0111, 1011 | |
Произведем склеивание по одной переменной между элементами соседних групп. В результате будут получены элементы кубического комплекса 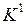 , которые также сведем в таблицу (табл. 4.12).
, которые также сведем в таблицу (табл. 4.12).
Таблица 4.12
| Кол-во единиц | 1-кубы |
| 01X0, 010X, | |
| 011X, 01X1, 10X1, 0X11, X011 | |
| X111, 1X11 |
Необходимо включать во все последующие таблицы 0-кубы и импликанты, не участвовавшие в склеивании, а затем исключать лишние по правилу поглощения.
Будем продолжать процедуру склеивания до тех пор, пока элементы очередного кубического комплекса могут склеиваться по одной переменной. При этом склеивание возможно только между i-кубами, имеющими одинаковые несущественные переменные (имеющими символ «Х» в одинаковых позициях).
Для рассматриваемого примера кубический комплекс 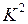 , сформированный путем склеивания элементов комплекса
, сформированный путем склеивания элементов комплекса 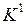 , представлен в табл. 4.13. Повторяющиеся 2-кубы исключены.
, представлен в табл. 4.13. Повторяющиеся 2-кубы исключены.
Таблица 4.13
| Кол-во единиц | 2-кубы |
 1 1
| 01ХХ, 01ХХ |
 2 2
| 10X1, ХХ11, ХХ11 |
Дальнейшее склеивание невозможно, поэтому кубический комплекс 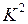 представляет собой совокупность простых импликант.
представляет собой совокупность простых импликант.
Составим импликантную матрицу Квайна (табл. 4.14) для нахождения минимальной совокупности простых импликант, представляющих в минимальной ДНФ все конституенты единицы исходной СДНФ. В рассматриваемом примере требуется найти минимальную совокупность 2-кубов, накрывающих все 0-кубы минимизируемой ПФ.
Таблица 4.14
| № | 0-кубы | 2-кубы | ||
| 01ХХ | 10X1 | ХХ11 | ||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + | + | |||
| + | + | |||
| + |
Из полученной импликантной матрицы видно, что все найденные на предыдущем этапе минимизации 2-кубы входят в минимальную совокупность простых импликант, т.е. все элементы кубического комплекса 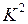 образуют минимальную ДНФ заданной ПФ.
образуют минимальную ДНФ заданной ПФ.
Окончательно,
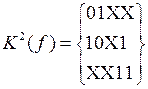 ,
,
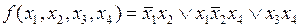 .
.
Полученное решение нетрудно проверить с помощью карты Карно (см. табл. 4.10).
4.4. Минимизация ПФ методом Блейка – Порецкого
Применение метода Квайна и метода Квайна –Мак-Класки для минимизации булевых функций требует преобразования произвольной ДНФ минимизируемой функции к СДНФ. В общем случае для осуществления такого преобразования можно пользоваться следующим соотношением: 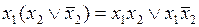 . Таким образом, для преобразования дизъюнктивного члена некоторой произвольной ДНФ необходимо выполнить умножение этого дизъюнктивного члена на дизъюнкцию прямого и инверсного значений отсутствующей переменной. В качестве примера можно привести следующее преобразование:
. Таким образом, для преобразования дизъюнктивного члена некоторой произвольной ДНФ необходимо выполнить умножение этого дизъюнктивного члена на дизъюнкцию прямого и инверсного значений отсутствующей переменной. В качестве примера можно привести следующее преобразование:
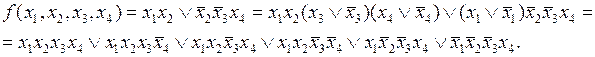
Как видно из этого условного примера, преобразование произвольной ДНФ к СДНФ требует довольно громоздких вычислений даже для функции четырех аргументов. Для функций большего числа аргументов процесс преобразования еще больше усложняется. Поэтому для минимизации функций, заданных произвольными ДНФ, удобно применять метод Блейка – Порецкого, не требующий задания ПФ в виде СДНФ.
Докажем справедливость следующего равенства, которое называется формулой обобщенного склеивания:
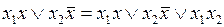 .
.
Равенство легко доказывается путем выполнения преобразований над его правой или левой частью. Преобразуем правую часть равенства.
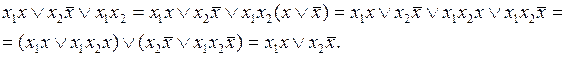
Поскольку в результате преобразований из правой части формулы обобщенного склеивания получена левая часть, то равенство доказано.
Метод Блейка – Порецкого основывается на утверждении: если в произвольной ДНФ минимизируемой ПФ произвести все возможные обобщенные склеивания и все возможные поглощения, то в результате будет получена сокращенная ДНФ исходной функции.
Для получения минимальной ДНФ необходимо составить импликантную матрицу Квайна и определить по ней минимальное покрытие единиц минимизируемой функции простыми импликантами.
Рассмотрим пример. Пусть подлежащая минимизации функция задана в следующем виде:
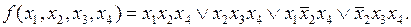
На первом этапе минимизации проведем всевозможные обобщенные склеивания.
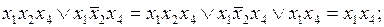
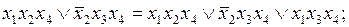
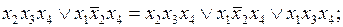
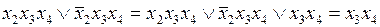 .
.
Исключив повторения элементарных произведений, получим ДНФ:
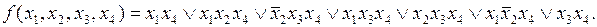
Выполнив все возможные поглощения, получим сокращенную ДНФ:
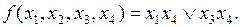
Построив импликантную матрицу (табл. 4.15), легко убедиться, что полученная сокращенная ДНФ является минимальной.
Таблица 4.15
| № | Исходные слагаемые | Простые импликанты | |
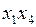
| 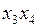
| ||
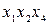
| + | ||
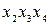
| + | ||
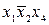
| + | ||
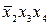
| + |
4.5. Минимизация ПФ,
заданных в конъюнктивной форме
Для минимизации ПФ, заданных в виде КНФ, можно использовать все вышеизложенные методы с незначительными отличиями. Отличия заключаются в записи соотношений склеивания и поглощения в конъюнктивной форме, а также в использовании некоторых понятий, характерных для КНФ.
Конституентой 0 называется функция, принимающая значение 0 на одном наборе значений аргументов. В конъюнктивной форме конституента 0 записывается как элементарная дизъюнкция всех переменных, причем переменная входит в дизъюнкцию с отрицанием, если ей соответствует цифра 1 в наборе. Например, конституента 0 ( 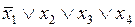 ) принимает значение 0 на наборе (1000).
) принимает значение 0 на наборе (1000).
Понятие импликанты и простой импликанты заменяется для КНФ на понятие имплиценты и простой имплиценты.
Имплицентой функции f называется функция, принимающая значение 0 на тех же наборах (или на части тех же наборов), на которых функция f принимает нулевое значение.
Простой имплицентой функции f называется имплицента, никакая часть которой не является сама по себе имплицентой f.
Для минимизации ПФ, заданной КНФ, как и в методах минимизации ДНФ, необходимо выполнить два этапа. На первом этапе осуществляется нахождение сокращенной КНФ, т.е. конъюнкции всех простых имплицент. При этом можно пользоваться соотношениями склеивания и поглощения, адаптированными для КНФ. Формула склеивания записывается как
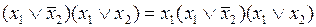 ,
,
а формула обобщенного склеивания как
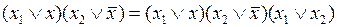 .
.
После нахождения всех возможных склеиваний следует выполнить все возможные поглощения по формуле
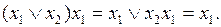
Для получения минимальной КНФ по сокращенной КНФ следует сформировать имплицентную матрицу Квайна, по которой определяется минимальное покрытие простыми имплицентами всех конституент 0 минимизируемой функции.
При минимизации ПФ с помощью карт Карно главное отличие заключается в поиске совокупностей, состоящих из 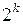 нулей. Все остальное можно оставить без изменений, но при этом в записи минимальной КНФ значения переменных следует инвертировать. Например, пусть подлежащая минимизации ПФ задана в виде карты Карно (табл. 4.16).
нулей. Все остальное можно оставить без изменений, но при этом в записи минимальной КНФ значения переменных следует инвертировать. Например, пусть подлежащая минимизации ПФ задана в виде карты Карно (табл. 4.16).
Таблица 4.16

| x2 | ||||
    x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Тогда ее минимальная КНФ запишется в следующем виде:
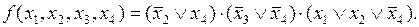
В общем случае до решения задачи минимизации ПФ нельзя сказать, какая из минимальных форм (ДНФ или КНФ) окажется проще. В некоторых случаях удобно использовать для получения минимальной ДНФ минимизацию по нулям. При этом будет получена минимальная ДНФ для функции 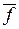 .
.
Дата добавления: 2014-12-27; просмотров: 3887;
