Этапы построения диаграммы разброса (рассеивания)

1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость. Было бы хорошо иметь, по меньшей мере, 30 пар данных.

2. Найдите максимальные и минимальные значения для х и у. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей осей х и у получились приблизительно одинаковыми (чтобы они уместились на экране компьютера или на стандартном листе бумаги), тогда диаграмму будет легче читать. При определении масштабов возьмите на каждой оси от 3 до 10 градационных делений и при обозначении этих делений используйте (для облегчения чтения) круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.

3. На экране компьютера (на отдельном листе бумаги) начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.

4. Нанесите на диаграмму все необходимые обозначения, например:

а) название диаграммы;

б) интервал времени сбора данных;

в) число пар данных;

г) названия и единицы измерения для каждой оси;

д) дата составления диаграммы;

е) имя (и прочие данные) человека, который составлял эту диаграмму.

Убедитесь, что перечисленные выше данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто строил диаграмму.

Типичные виды диаграмм разброса (рассеивания) приведены на рис. 3.8.

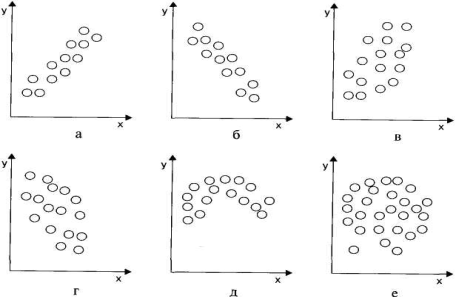
Рис. 3.8. Типичные виды диаграмм разброса (рассеивания): а — сильная положительная корреляция; б — сильная отрицательная корреляция; в — слабая положительная корреляция; г — слабая отрицательная корреляция; д — криволинейная корреляция; е — отсутствие корреляции.

После построения диаграммы рассеивания необходимо изучить связи между х и у, но для установления силы связи в количественных терминах нужно вычислить коэффициент корреляции в соответствии со следующим определением:

где п — число пар данных; хi, yi — собранные статистические данные; x, y — средние арифметические значения соответствующих факторов х и у; r— коэффициент корреляции, который принимает значение из диапазона -1 ≤ r ≤ 1.

Если абсолютное значение r окажется больше 1, то совершенно ясно, что произошла ошибка и вы должны пересчитать результат.

При наличии корреляционной зависимости можно осуществлять контроль только одной (любой) из двух характеристик.